|
1 L
259 |
Направленное перемещение жидкости в пористом теле под действием приложенной разности потенциалов (электроосмос) удобно изучать с помощью прибора, схематически показанном на рис. IV. 11. Прибор представляет собой U-образную трубку, в одно колено которой впаян капилляр 1 для точного определения количества протекающей жидкости, в другом — между
Рис. IV. ll. Прибор Для наблюдения осмоса:
І — капилляр-; 2 — мембрана
17*
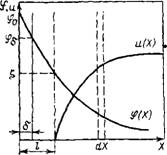
Рис. IV 12. Изменение потенциала <р и скорости течения жидкости и с расстоянием Х от поверхности капилляра
Электродами располагается пористое тело 2 (мембрана) из силика — геля, глинозема и других материалов.
В прибор наливают воду или водный раствор и отмечают уровень жидкости в капилляре. Если к электродам приложить разность потенциалов, то противоионы диффузного слоя, энергетически слабо Связанные с поверхностью твердой фазы (мембрана), будут перемещаться к соответствующему электроду н благодаря молекулярному трению увлекать за собой дисперсионную среду (водный раствор). Вполне естественно предположить, что чем больше потенциал диффузного слоя, тем больше переносчиков зарядов, тем выше скорость перемещения жидкости в пористом теле. Скорость течения жидкости и ее направление при постоянной напряженности электрического поля определяются свойствами мембраны и раствора. Таким образом, уже качественное изучение электроосмоса позволяет однозначно определить знак ^-потенциала, а количественные измерения — установить зависимость между скоростью переноса жидкости и £-потенциа- лом. Изменяя состав и свойства дисперсионной среды, можно проследить за изменением структуры двойного электрического слоя по изменению значения электрокинетического потенциала.
Для получения наиболее простого уравнения, связывающего скорость относительного движения фаз с параметрами дисперсионной среды (вязкость, диэлектрическая проницаемость), двойного электрического слоя (^-потенциал) и внешнего электрического поля (напряженность), необходимо задаться некоторыми ограничениями: 1) толщина двойного электрического слоя значительно меньше радиуса пор, капилляров твердой фазы (радиуса кривизны поверхности твердой фазы); 2) слой жидкости, непосредственно прилегающий к твердой фазе, неподвижен, движение жидкости в порах твердой фазы ламинарное и подчиняется законам гидродинамики; 3) распределение зарядов в двойном электрическом слое не зависит от приложенной разности потенциалов; 4) твердая фаза является диэлектриком, а жидкость проводит электрический ток.
|
|
Рис. IV.12 иллюстрирует изменение потенциала ф и скорости движения жидкости и в капиллярах пористого тела с изменением расстояния от межфазной поверхности. Направленное перемещение жидкости, вызванное внешним электрическим полем напряженностью Е, уравновешивается действием возникающей
силы трения. В стационарном состоянии общая сила, действующая на любой сколь угодно малый слой жидкости, равна нулю, и он движется с постоянной скоростью параллельно границе скольжения.
Электрическая сила, действующая на слой жидкости dx (в расчете на единицу площади поверхности), равна
(Р ф
DF3n~ Edq = Ер dx — — Јe0eDx (IV.71)
Где Dq — заряд слоя жидкости Dx; p — объемная плотность заряда, выраженная в соответствии с уравнением Пуассона (11.113).
Сила трения и ее дифференциал, приходящиеся на единицу площади (согласно закону Ньютона), составляют:
Du Аги
Frp — n-fa и dFTp — r]-j^-dx (IV.72)
При установившемся движении (в стационарном состоянии) DF3A = DFTр, т. е. приравнивая (IV.71) и (IV.72), получим
|
(IV.73) |
D2u £е,0е
Dx2 г) dx2
Так как в обе части равенства (IV.73) входят производные по А’, а коэффициент пропорциональности при интегрировании принимается постоянным, то решение уравнения (IV.73) сводится фактически к определению граничных условий интегрирования.
Пределы интегрирования легко определить из рис. IV.12. При Х=1, т. е. на границе скольжения, имеем ф = £ и и = 0; при х^=оо, т. е. в объеме р ЗСТ ВОр 3, фоо = 0 и Uoo = Uo, A (dq>/dx) Оо = 0 и (du/dx)aО = 0. Таким образом, после первого интегрирования вид уравнения (IV.73) практически ие изменится, только вместо вторых производных получим первые производные по Х знак минус останется в уравнении, так как обе первые производные при х—>-оо параллельно стремятся к нулю. При подстановке пределов в уравнение, полученное после второго интегрирования, необходимо только изменить знак «—» на «+», что связано с уменьшением потенциала до нуля при х—>-оо и увеличением скорости движения жидкости в этом направлении до щ. Окончательно получим следующее выражение для постоянной линейной скорости жидкос^л относительно мембраны:
И0 = е0еЕ£/ц (IV. 74)
Это классическое выражение для скорости движения жидкости при электроосмосе можно получить и на основе представ — — лений двойного электрического слоя как плоского конденсатора, что и было сделано еще Гельмгольцем. Более строгий вывод соотношения (IV.74) был дан Смолуховским, поэтому урав
нение (IV.74) носит название уравнения Гельмгольца — Смолуховского.
Скорость движения дисперсионной среды, отнесенная к единице напряженности электрического поля, называется электроосмотической подвижностью:
И30 = ио/Е=ЄоЄ^/і) (IV.75)
Уравнение Гельмгольца — Смолуховского чаще записывают относительно потенциала:
(IV-76)
В уравнения (IV.74) — (IV.76) входит электроосмотическая линейная скорость, которую при обработке экспериментальных данных удобнее заменить на объемную скорость течения жидкости V = U0S (где S — поперечное сечение всех капилляров в пористой мембране). Необходимо помнить, что уравнение Гельмгольца— Смолуховского выведено, исходя из допущения, что вся масса жидкости в капиллярах перемещается со скоростью Ыо. Однако скорость перемещения жидкости в двойном электрическом слое меньше, чем и0. Следовательно, уравнение (IV.74) справедливо в Оюм случае, если размеры капилляров значительно больше толщины двойного слоя.
Чтобы не вводить в уравнение (IV.76) поперечное сечение капилляров S, воспользуемся законом Ома. Тогда отношение линейной скорости движения жидкости к напряженности электрического поля можно преобразовать следующим образом:
И0 vL VL vLxs m ~T~ sU — sIR s/L / UV.//J
Где L — расстояние между электродами; U — внешняя разность потенциалов; / — сила тока; R — электрическое сопротивление; х — удельная электропроводность.
Подставляя выражение Чо/Е в уравнение (IV.76), получим:
T-5- <>"»>
Уравнение (IV.78) позволяет по экспериментально определяемым значениям величин и, х, Tj и / рассчитать электрокине — тнческий потенциал.
Анализ соотношения (IV.78) показывает, что оно справедливо как для единичного цилиндрического капилляра, так и для системы капилляров различной формы, поскольку в это уравнение не входят их геометрические параметры. Это уравнение применимо, если выполняются все условия, сформулированные Вьщіе.
Если радиус капилляра сопоставим с толщиной двойного электрического слоя, что имеет место в микропористых капиллярных системах, то значение удельной электропроводности х в объеме раствора, входящей в уравнение (IV.78), не будет соответствовать значению электропроводности раствора внутрн капилляра, и при расчете ^-потенциала необходимо вводить поправку на поверхностную проводимость. Поверхностная проводимость представляет собой приращение проводимости раствора в капилляре вследствие наличия двойного электрического слоя, и общая проводимость может быть в несколько раз больше объемной. Поэтому при вычислении значений ^-потенциала по результатам исследования электроосмоса, происходящего в системе достаточно узких капилляров и разбавленных растворов, в расчетную формулу вместо х подставляют выражение и+XsG/s (где и — удельная объемная электропроводность; Xs—поверхностная проводимость; 0 — длина окружности капилляра с сечением s). Поправка xs0/s всегда положительна, поэтому истинные значения ^-потенциала, т. е. рассчитанные с введением поправки, будут больше. Поправку на поверхностную проводимость определяют, измеряя электрическое сопротивление капилляров, заполненных разбавленным и концентрированными растворами электролитов, или сравнивая результаты с полученными по уравнению (IV.76), в которое не входит электропроводность жидкости в капилляре. Поверхностной проводимостью можно пренебречь, если размеры капилляров велики по сравнению с толщиной двойного слоя.
Следует отметить, что в пределах двойного электрического слоя значения диэлектрической проницаемости и вязкости дисперсионной среды иные по сравнению со значениями этКх величин в объеме раствора, и это различие становится особо ощутимым, если толщина двойного слоя и радиус капилляров твердой фазы соизмеримы.
 2 ноября, 2012
2 ноября, 2012  admin
admin 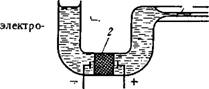
 Опубликовано в рубрике
Опубликовано в рубрике 