С термодинамической точки зрения адсорбция является самопроизвольным процессом выравнивания химических потенциалов веществ в объеме системы и межфазном (поверхностном) слое. Этот процесс происходит вследствие стремления к минимуму поверхностной энергии или энергии Гиббса всей системы.
|
12» |
Адсорбцию можно рассматривать как взаимодействие молекул адсорбата с активными центрами поверхности адсорбента. Такое представление этого явления оказалось достаточно общим и удобным, особенно для адсорбции на твердых адсорбентах, когда возникают трудности экспериментального определения межфазного натяжения. Кроме того, такая интерпретация адсорбции открывает возможность изучения природы адсорбционного взаимодействия. Если отсутствует химическое
9 Фролов Ю. Г.
Взаимодействие адсорбата с адсорбентом, то адсорбция, как правило, является результатом самопроизвольного уменьшения поверхностной энергии системы, выражающегося в компенсировании поля поверхностных сил. При наличии специфического сродства адсорбата к адсорбенту, адсорбция обусловлена самопроизвольным уменьшением энергии Гиббса всей системы, что может привести даже к увеличению поверхностной энергии. Это возможно в том случае, если изменение химической составляющей энергии Гиббса системы больше изменения поверхностной энергии. При химической адсорбции между адсор — батом и адсорбентом образуется химическая связь, и они теряют индивидуальность.
Процессы адсорбции классифицируют в соответствии с типом взаимодействия адсорбата с адсорбентом. Физико-химическая классификация основывается на том положении, что перераспределение компонентов между объемной фазой и поверхностным слоем может происходить под действием физических сил или в результате химической реакции между адсорбатом и адсорбентом. Химическую реакцию в этом случае можно представить либо как химическое присоединение атомов (молекул), либо как ионообменное взаимодействие. Таким образом, согласно физико-химической классификации различают Физическую (молекулярную) адсорбцию, хемосорбцию (химическое присоединение атома, молекулы) и ионный обмен. В данном разделе рассматривается, главным образом, физическая адсорбция газов и паров.
При физической адсорбции взаимодействие адсорбента и адсорбата осуществляется за счет сил Ван-дер-Ваальса и водородных связей. Эти адсорбционные силы обеспечивают притяжение атомов (молекул); на очень близком расстоянии проявляются короткодействующие силы отталкивания.
Напомним, что силы Ван-дер-Ваальса включают три вида взаимодействия. Основным из них является дисперсионное взаимодействие, проявляющееся между неполярными молекулами. Это так называемый дисперсионный эффект (действие сил Лондона). Силы взаимодействия между неполярными молекулами возникают вследствие того, что флуктуации электронной плотности в одном атоме индуцируют подобные флуктуации в соседнем атоме. Резонанс таких флуктуации приводит к уменьшению общей энергии системы, обусловленному притяжением атомов. Очевидно, что такие силы имеют общий характер и могут возникать между любыми атомами, что и объясняет их универсальность.
Межмолекулярное дисперсионное взаимодействие усиливается при наличии у молекул постоянных диполей. Диполь-дипольное взаимодействие (действие сил Кеезома) называется ориентационным эффектом. Чем больше дипольные моменты взаимодействующих молекул, тем больше составляющая ориентационного эффекта.
При взаимодействии между полярной и неполярной молекулами проявляется индукционный эффект (действие сил Дебая). Индукционные силы способствуют усилению притяжения благодаря тому, что полярная молекула
индуцирует диполь в неполярной молекуле. Этот эффект тем значительнее, чем больше поляризуемость молекул.
Если оценить вклады отдельных эффектов, обусловленных действием составляющих ван-дер-ваальсовых сил, в общую энергию притяжения молекул, то оказывается, что доля индукционного эффекта составляет не более 5%. Доля орнентационного эффекта в значительной степени зависні от дипольных моментов взаимодействующих молекул, но даже для молекул, обладающих очень большими дипольнымн моментами, например, для молекул аммиака и воды, ориентационный эффект приблизительно равен дисперсионной составляющей. Таким образом, для молекул с небольшими дипольнымн моментами основной вклад в энергию взаимодействия внося; дисперсионные силы. Характерно, что для всех трех составляющих сил Ван-дер-Ваальса выполняется один и тот же закон изменення энергии прп — тяжения от расстояния
U„SAr) = — С/г" (Ш. П
Где С — константа, которая рассчитывается по соответствующим для каждого эффекта формулам.
На очень близких расстояниях при перекрывании электронных оболочек атома возникает отталкивание, энергию которого представляют эмпирическим соотношением
Где Ь—эмпирическая константа; т — константа, обычно принимаемая равной 12; такое большое значение показателя степени показывает на необходимость учета сил отталкивания только на очень близких расстояниях.
Полную потенциальную энергию двух взаимодействующих атомов (молекул) удовлетворительно описывает уравнение Леннарда — Джонса, объединяющее соотношения (III. I) и (III.2):
L'(r)=fo/r12 — С//-е (III .3»
При адсорбции происходит взаимодействие между атомом (молекулой) адсорбата с поверхностью адсорбента, т. е. с большим числом атомов (молекул) адсорбента. Поэтому зависимость энергии притяжения при адсорбции от расстояния иная, чем описываемая по уравнению (III.3). Это объясняется тем, что дисперсионные силы, вносящие основной вклад во взаимодействие, обладают свойством аддитивности. Поэтому если один атом взаимодействует с системой атомов из 2,3,4 и т. д. атомов, то энергия взаимодействия соответственно в 2,3,4 и т. д. раз больше, чем энергия двух взаимодействующих атомов (III. 1).
Таким образом, чтобы рассчитать энергию взаимодействия при адсорбции, необходимо провести суммирование энергий взаимодействия адсорбирующегося атома с каждым атомом ад
|
|
|
9* |
|
131 |
Рис. III. I. К определению энергии притяжения атома А твердым адсорбентом
сорбента. Расчет упрощается при замене суммирования на интегрирование. При этом необходимо предположить, что поверхность адсорбента имеет бесконечно большую площадь по сравнению с площадью, занимаемой адсорбированным атомом (молекулой) и что действуют только аддитивные дисперсионные силы. На рис. II 1.1 представлена схема, поясняющая расчет энергии указанного взаимодействия. Величина х обозначает расстояние адсорбирующегося атома А от поверхности адсорбента, а г — расстояние атома А от отдельных атомов адсорбента. Так как общая энергия взаимодействия при адсорбции Uаде определяется суммой энергии взаимодействия адсорбированного атома со всеми атомами в объеме адсорбента, то
DU»:lc~ l!„,,ndY (111.4)
Где п — число атомов (молекул) в единице объема адсорбента: DV—приращение объема адсорбента.
Величину DV можно определить через поверхность шарового сегмента:
S = 2л/7( или л = 2яг (г — — л-)
Тогда
DV — 2nrir — x)dr (II 1.51
Подставляя в уравнение (III.4) выражение величин U„р и dV из уравнений (III. 1) и (III.5), получим:
С :2пСп DUaac = —~рг п2лг(г — x)dr -pj— (г — x)dr
Проведем интегрирование в пределах расстояния от г=х до Г —оо
TOC o "1-3" h z ОС С L-‘ оо
F аде =* — 2лС п J Dr T= — 2ПСп ^ J* -г! г — J" =»
X XX
Ґ Х [
•= ~ 2пСп (з^г — ^г =» ~ 2пСп -12р-
V 4 *
"Окончательно получим:
F/адс— пСп/Ш3) (II 1.6)
Итак, энергия притяжения при адсорбции убывает с увеличением расстояния, причем"i/адс зависит от расстояния х в третьей степени вместо шестой, как это имеет место при взаимодействии двух атомов. Такая зависимость указывает на более медленное уменьшение энергии притяжения при адсорбции и на дальнодействие адсорбционных сил.
Рис. 111.2. Потенциальные кривые адсорбции арі она на графите (I) и взаимодейст- 8 Иия атомов аргона и углерода (2)
I 4
Уравнение (III.6) было исполь — зовано Лондоном, а затем и други — 0 ми учеными для экспериментально — * го доказательства дисперсионной ь природы адсорбционных сил и свя — зи энергии адсорбции со свойствами адсорбированных молекул и адсорбента.
Полную потенциальную энергию взаимодействия при адсорбции можно выразить уравнением
U (.v) = Ь/хт — яСп;‘ G. v3». (111.7)
На рис. III.2 приведена зависимость потенциальной энергии взаимодействия атома аргона с поверхностью графита от расстояния (кривая /); для сравнения показана кривая взаимодействия отдельных атомов аргона и углерода (кривая 2). Кривые 1 и 2 подобны, однако, как следует из рисунка, действие адсорбционных сил простирается на более дальнее расстояние. При расчете кривых расстояния х и г были выбраны произвольно. В точке минимума кривых производные DU/Dx = = 0, т. е. сила взаимодействия F — DU/Dx = 0, что означает, равновесие адсорбции в данной точке. Потенциальная энергия системы в точке минимума практически равна энергии адсорбции.
Из рассмотрения природы адсорбционного взаимодействия вытекает практически важный вывод о значительно лучшей адсорбции веществ в трещинах и порах, когда проявляется преимущественно дисперсионное взаимодействие, так как вблизи адсорбированной молекулы находится большее число атомов твердого тела. Кроме того, из уравнений (III.6) и (III.7) следует, что чем большее. число атомов содержит молекула адсорбата, тем с большей энергией она будет притягиваться к адсорбенту. Если же в адсорбционное взаимодействие значительный вклад вносят электростатические силы, то в щелях и порах положительные и отрицательные заряды компенсируют друг друга и наибольший потенциал оказывается на выступах, где и будет преобладать адсорбция, особенно при образовании водородных связей (адсорбция воды, метанола и др.).
 2 ноября, 2012
2 ноября, 2012  admin
admin 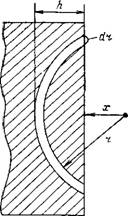
 Опубликовано в рубрике
Опубликовано в рубрике 