Этот метод основан на наблюдении крупной капли жидкости на плоской поверхности и воздушного пузырька (тоже большого размера) в той же жидкости.
|
Рис. 10 |
Пусть на горизонтальной плоскости (рис. 10) образована большая капля исследуемой жидкости, настолько большая, что ее поверхность всюду, кроме краев, плоская, и пусть ![]() краевой угол у границы капли. Условием равновесия капли является равенство абсолютных значений сил, стремящихся превратить ее в тонкую пленку, и сил, стремящихся придать ей сферическую форму. Растянуть каплю в тонкую пленку стремится, во-первых, сила тяжести и, во-вторых, сила поверхностного натяжения на границе между жидкостью и твердой подложкой. Сферическую же форму капле стремится придать сила поверхностного натяжения на поверхности жидкости.
краевой угол у границы капли. Условием равновесия капли является равенство абсолютных значений сил, стремящихся превратить ее в тонкую пленку, и сил, стремящихся придать ей сферическую форму. Растянуть каплю в тонкую пленку стремится, во-первых, сила тяжести и, во-вторых, сила поверхностного натяжения на границе между жидкостью и твердой подложкой. Сферическую же форму капле стремится придать сила поверхностного натяжения на поверхности жидкости.
Рассмотрим вертикальное сечение капли, перпендикулярное к плоскости чертежа, и выделим в этом сечении площадку высотой H (высота капли) и длиной в 1 см. Благодаря силе тяжести на этом сечении действует гидростатическое давление. Среднее его значение равно ![]() , где
, где ![]() — плотность жидкости и g — ускорение свободного падения. Сила же F, вызванная им, равна
— плотность жидкости и g — ускорение свободного падения. Сила же F, вызванная им, равна 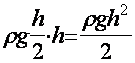
(площадь выделенной площадки равна H!). Направление этой силы показано на рис. 10, А.
Горизонтальная составляющая F ‘ поверхностного натяжения на границе жидкости и подложки, отнесенная к единице длины, равна ![]()
![]() . Направлена она так же, как сила F, и вместе с ней стремится превратить каплю в пленку. Этим двум силам противостоит сила поверхностного натяжения на поверхности жидкости F", Направленная против них и равная
. Направлена она так же, как сила F, и вместе с ней стремится превратить каплю в пленку. Этим двум силам противостоит сила поверхностного натяжения на поверхности жидкости F", Направленная против них и равная ![]() (на единицу длины). Таким образом, условие равновесия капли можно записать в виде
(на единицу длины). Таким образом, условие равновесия капли можно записать в виде
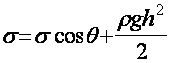
Или
|
(7) |
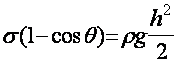
Рассмотрим теперь воздушный пузырек в той же жидкости (рис. 10,6). Если пузырек достаточно велик, чтобы его «дно» было плоским, то рассуждения, подобные только что приведенным, показывают, что условием равновесия пузырька будет равенство
|
(8) |
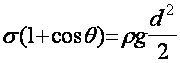
Где D — Высота пузырька. Складывая (7) и (8), получим:
|
(9) |
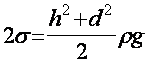
Следовательно, для определения коэффициента поверхностного натяжения ![]() достаточно измерить высоты капли и пузырька.
достаточно измерить высоты капли и пузырька.
Интересно, что этот же опыт может быть использован и для определения краевого угла ![]() . В самом деле, если вычесть (7) из (8), то получим:
. В самом деле, если вычесть (7) из (8), то получим:
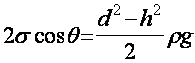
Но по уравнению (9) 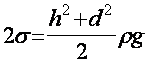 следовательно, для
следовательно, для ![]() получается равенство
получается равенство
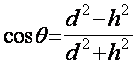
|
Рис. 11 |
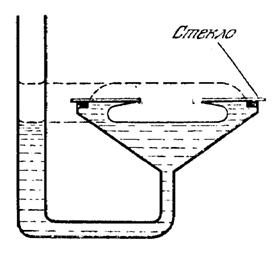
Значит, для определения ![]() тоже требуется измерить только D и H. Экспериментально D и H Определяются с помощью манометра особом формы, показанной на рис. 11. После тщательной очистки манометр наполняется исследуемой жидкостью, после чего часть жидкости отсасывается так, чтобы образовался пузырек достаточного размера. Затем делается отсчет по манометру и этим определяется положение «дна» пузырька. После этого в прибор добавляют жидкость, чтобы на поверхности стекла, покрывающего широкое колено манометра, образовалась большая капля жидкости (на рис. 11 показана пунктиром). Новый отсчет по манометру даст положение основания капли. Наконец, с помощью специального прибора (сферометра) определяют высоту капли H. Зная толщину стекла, можно теперь из двух отсчетов по манометру определить D И вычислить как коэффициент поверхностного натяжения, так и краевой угол.
тоже требуется измерить только D и H. Экспериментально D и H Определяются с помощью манометра особом формы, показанной на рис. 11. После тщательной очистки манометр наполняется исследуемой жидкостью, после чего часть жидкости отсасывается так, чтобы образовался пузырек достаточного размера. Затем делается отсчет по манометру и этим определяется положение «дна» пузырька. После этого в прибор добавляют жидкость, чтобы на поверхности стекла, покрывающего широкое колено манометра, образовалась большая капля жидкости (на рис. 11 показана пунктиром). Новый отсчет по манометру даст положение основания капли. Наконец, с помощью специального прибора (сферометра) определяют высоту капли H. Зная толщину стекла, можно теперь из двух отсчетов по манометру определить D И вычислить как коэффициент поверхностного натяжения, так и краевой угол.
Коэффициенты поверхностного натяжения некоторых жидкостей:
|
Жидкость |
Температура |
Поверхностное натяжение Н/М |
|
Раствор мыла в воде Спирт Эфир Ртуть Золото Жидкий водород Жидкий гелий |
20 20 20 25 20 1130 -253 -269 |
0,0725 0,040 0,022 0,017 0,470 1,102 0,0021 0,00012 |
 19 декабря, 2012
19 декабря, 2012  admin
admin 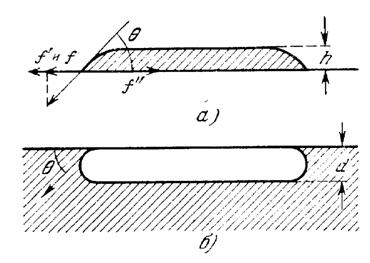
 Опубликовано в рубрике
Опубликовано в рубрике 