Лако-красочные материалы — производство

Различают три режима, характеризующих поведение частиц твердой фазы в жвдкой среде [117]. При малом содержании твердой фазы влияние столкновений частиц невелико, и поведение частиц определяется вяз­костью среды. При некотором промежуточном содержании частиц число столкновений между ними увеличивается,-инерционные силы становятся более заметными по сравнению с вязкостью среды. При высоком содер­жании частиц твердой фазы их перемещения настолько тормозятся, что в динамическом поведении среды преобладает межчастичный контакт. Если в пасту вводится небольшое количество диспергирующих тел сфе­рической формы, то в результате разрушения структуры несколько сни­жается эффективная вязкость системы — эффект Томса, с увеличением количества этих тел они становятся составляющими новых структурных образований. Относительное смещение мелющих тел разрушает эти обра­зования и происходит снижение эффективной вязкости с одновремен­ным разрушением пигментных агрегатов.

Предполагается, хчто в диспергаторах, в которых течение системы (паста и диспергирующие тела) осуществляется под внешним воздей­ствием, процесс имеет вероятностный характер и зависит от вида тече­ния, которое определяется конструктивными особенностями диспергиру­ющего аппарата.

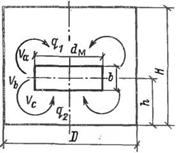
Для описания гидродинамических процессов в цилиндрических аппаратах с мешалками предложена [118; 119, с. 11] двухконтурная циркуляционная модель с переменной структурой. Эта модель составляется следующим образом:

1. Зона мешалки, где наблюдается наибольшая степень турбулизации, пред­ставляется в виде одной ячейки идеального смешения. Эта зона геометрически
представляется цилиндром, симметричным оси и положению мешалки (рис. 3.1), объем ее можно определить по уравнению:

Уь= %2 ль(5й2 + + Д<*М) (3-1)

2. Весь остальной объем аппарата разделяется положением мешалки на две зо­ны: верхнюю и нижнюю, которые соединены двумя циркуляционными контурами, пересекающимися в зоне мешалки. В зависимости от положения мешалки каждая зона аппроксимируется переменным числом ячеек. Общий объем ячеек в каждом из контуров можно определить из соотношений:

TOC o "1-5" h z Уа=0,25пБЦН-Н)-0,бУь (3.2)

Гс = 0,257^/2-0,514, (3.3)

3. Поток, создаваемый мешалкой, делится на два вторичных потока, образу­ющих верхний и нижний циркуляционные контуры. Эти вторичные потоки нахо­дят из соотношения:

Ч,/Ч2 = Л/(»-Л) (34)

Основной поток <?, создаваемый мешалкой, вычисляют по уравнению насосной производительности. Для мешалок с лопастями:

Д=кп(11,Ь (3-5>

где к — коэффициент, зависящий от числа лопаток мешалки; п — частота вращения мешалки.

Количество жидкости, притекающей к гладкому диску в осевом направлении, определяется из условия:

Я, = 0,219ноПе~°’2 (3.6)

Где К — радиус диска; ы — его угловая скорость.

Кратность циркуляции, являющаяся отношением насосной производительно­сти к объему среды, определяет качество обработки и отражает затраты работы на обработку единицы объема среды. Между условиями работы мешалок и свойства­ми создаваемого ими потока существует непосредственная связь, отражающаяся на интенсивности протекающих процессов.

В цилиндрических сосудах с лопастными мешалками течение рассматривается как комбинированный вихрь Ренкина, который представляет собой совокупность цилиндрического вихря конечной длины и вихря, уходящего в бесконечность области динамического вращения жидкости вокруг него. Радиус цилиндрического вихря зависит от радиуса окружности, охватываемой мешалкой. Зависимость ради­уса центрального вихря г в от центробежного критерия Рейнольдса Яец при радиусе мешалки г м можно представить выражением:

Гв/гм =Кец/(103+ 1,6Кец) (3.7)

Эпюра изменения окружной скорости по­тока н»х отражает ее возрастание с ростом ра­диуса потока в пределе до г = г м и последу­ющее снижение в связи с внутренним трением (рис. 3.2). Характер движения жидкости в ци­линдрических сосудах с дисковыми и диско­зубчатыми мешалками отражается на давлении

Рис« 3.1. Схема двухконтурной циркуляцион­ной модели.

Рис. 3.3. Изменение давления под дисковой мешалкой.

Рис. 3.4. Изменение текущего радиуса-вектора.

Потока р в зоне сосуда, находящейся под мешалкой (рис. 3.3) [94, с. 78]. В центре зоны вращения дисковой мешалки возникает разрежение. По мере удаления от оси сосуда нарастает давление, которое достигает наибольшего значениия на периферии диска, а затем снижается (в пределе до нуля) у стенок сосуда.

Градиент скорости и, следовательно, напряжение сдвига от действия мешалок зависит не только от степени т отклонения течения данной системы от ньютонов­ского, но и от конструктивных особенностей аппарата, характеризуемых отношени­ем диаметра мешалки к диаметру сосуда: Гд =гм! гс. На границе зон скорость сдви­га приобретает значение:

Т-.2/тп

У=-47Г-^-т5^ (3.8)

1 т 1-Грг/тп

Направленность линии токов как для гомогенных, так и для гетерогенных систем не зависит от частоты вращения перемешивающего устройства и его типа [118;119,с. П]. Превалирующие тангенциальные токи деформируются радиальной составляющей, и результирующая линия токов приобретает вид логарифмической спирали. Значение текущего радиуса-вектора описывается в конечном виде урав­нением:

Г =/?ехр(-сгг©,у>) (3.9)

Где © — угол между касательной к проекции спирали на плоскость, перпендикуляр­ную оси вращения, и радиусом-вектором в данной точке проекции (рис. 3.4).

Гидродинамика флокулированных и вязко-пластичных систем описана в рабо­тах [120; 121; 122].

Скорость сдвига и соответствующее ей напряжение сдвига в объеме цилиндрического аппарата — величина переменная. В поперечном сечении аппарата наибольшая скорость сдвига достигается в кольцевой плоско­сти, осевая линия которой совпадает с концом мешалки. По мере удале­ния от плоскости действия мешалок в результате внутреннего трения в перемешиваемой системе и торможения потока скорость сдвига и соот­ветствующее напряжение сдвига уменьшаются. Следовательно, для одной и той же системы при неизменной частоте вращения мешалок диспергато — ра напряжение^сдвига различно в разных точках пространства и зависит от радиуса дисковых мешалок и шага между ними.

В бисерных диспергаторах количество циркуляционных контуров и ячеек идеального смешения зависит от количества дисков на сборных мешалках. Гидродинамика потока здесь усложняется передвижением пасты под действием шестеренчатых насосов, а также изменением ее фи­зических свойств в результате дезагрегации и изменения температуры. На гидродинамику потока и реологические особенности пигментных паст весьма значительно влияет наличие диспергирующих тел, которые нару­шают сплошность структуры пасты, что вызывает изменение ее вязко — упругих свойств. Напряжение сдвига здесь определяется кажущейся вяз­костью системы паста — диспергирующие тела, которая, в свою очередь, определяете» эффективной вязкостью пигментной пасты, физическими свойствами диспергирующих тел (плотностью, размерами, способностью смачиваться растворами пленкообразователей) и адгезионными свойст­вами пасты.