Для проведения анализа гидродинамических проблем, связанных с течением жидкости через межлопастные пространства ротора мешалки, можно с некоторым приближением воспользоваться упрощенной теорией вихревых насосов [241]. Эта теория предполагает полную симметричность течения относительно оси вращения ротора
(симметричное осевое течение). При таком течении скорости жидкости являются функциями двух координат г и Z. Осевое симметричное течение можно разделить на два течения — меридиональное, в котором частицы жидкости перемещаются в плоскостях, проходящих через ось ротора, и окружное, в котором частицы жидкости перемещаются по концентрическим с осью Z окружностям, расположенным в плоскостях, перпендикулярных к этой оси. В роторах с радиальным течением меридиональные составляющие становятся радиальными, а в роторах с осевым течением — осевыми.
Дальнейшее упрощение состоит в том, что течение жидкости через межлопастной канал ротора рассматривается как движение частицы жидкости вдоль центральной линии канала. Таким образом, не учитывается распределение скоростей жидкости в поперечных сечениях канала. Следовательно, скорости жидкости становятся функцией только одной координаты — радиуса г. Рассмотрим течение жидкости для мешалок, создающих радиальный поток, а затем для мешалок, создающих осевой поток.
Мешалки, создающие радиальный поток жидкости. Обратимся к графику скоростей жидкости в плоскости вращения мешалки,
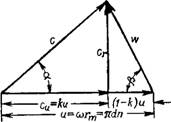
Рис. III-22. Треугольник скоростей на выходе из идеального ротора.
С — абсолютная скорость; и = сOrm= Ndn — окруж— ная скорость (уноса); W — относительная скорость; сг — радиальная составляющая абсолютной скорости; си = с Cos а—окружная составляющая (тангенциальная) абсолютной скорости; а — угол, под которым жидкость покидает ротор; 0 — угол наклона конца лопаток; H = сц/м = юс/ю — коэффициент окружных скоростей (отношение угловой скорости жидкости к угловой скорости мешалки). Величина H определяет тип потока: при H = 1 поток является чисто тангенциальным (окружным), при K = 0—чисто радиальным.
Создающей радиальное течение. Если вал вращается с определенной постоянной угловой скоростью (о, то можно говорить об абсолютном движении жидкости (рассматриваемом относительно неподвижной оболочки, например стенки аппарата) и об ее относительном движении (рассматриваемом относительно вращающегося вала).
Частицы жидкости покидают лопатки мешалки с абсолютной скоростью с, направленной под углом а к окружной скорости и. Состояние движения жидкости на выходе из мешалки описывает так называемый треугольник скоростей (рис. II1-21 и III-22).
|
Рис. III-21. Схема протекания жидкости через идеальный ротор. |
|
|
Для данного ротора известны такие величины, как высота подъема и и угол наклона лопаток р. Остальные величины следуют из
Двух указанных и связаны с конкретным условием работы мешалки. Представленный треугольник скоростей относится к так называемому идеальному случаю при числе лопаток Z = оо и отсутствии энергетических потерь потока.
В реальной мешалке с конечным числом лопаток не существует идеального течения жидкости в межлопастных пространствах, вследствие чего меняется треугольник скоростей (уменьшается угол (3 и увеличивается угол а), т. е. снижается значение коэффициента к. Насосный эффект для идеальной мешалки с радиальным течением жидкости представляет произведение скорости на поверхность цилиндра:
Vp = ndbcr (II1-31)
Радиальную составляющую сг рассчитывают по треугольнику скоростей:
|
‘ с2 с Ческий напор мешалки Hf = Ucu со значением Н — ——j — ~ (урав- |
Cr=sinp У с2 + «2_2сцм (III-32)
Абсолютную скорость с можно рассчитать, сравнивая теорети — кий напор мен нение Вернули):
= + (II1-33)
Где с2/2 — динамический напор; сЦ2 — статический напор, вызванный центробежной силой. Отсюда получаем:
C = V2ucu — cl (111-34)
После подстановки уравнения (III-34) в зависимости (III-31) и (III-32) и при условии, что Cu = ки и и = Ndn, имеем:
Сг = лDn sin р Vi — № (111-35)
И
= sinp/l-A-2 (II1-36)
При использовании семейства геометрически подобных мешалок, для которых Bid = Ib = const, можно написать:
V}= n*ibnd* sin p Yi — Л» (II1-37)
|
. а с, л Sin В = ■ |
Уравнение (111-36) было выведено в таком виде впервые Ван де Вуссе [216]. Ухл и Грей [206] несколько модифицировали его, заменив функцию sin (3 коэффициентом к:
F—
W У С2-|-М2_2ысц Если с2 = 2Иси — с и си = ки, то
8 Заказ 1259 113
Уравнение (III-36) примет вид:
V* =Ji4ndzV 2k(i~ К) (III-39)
Или
V* = n*IBndsV2k(L~ К) (II1-40)
По последнему уравнению рассчитывают коэффициент насосного эффекта
V% ________
Lp = ~^W== n2ibV2k(l-k) (II1-41)
Который приобретает постоянное значение только для ц = const и к = const.
Уравнения (III-36), (111-37), (III-39) и (111-40) можно применять для идеального ротора. Поэтому они имеют главным образом теоретическое значение, но тем не менее могут также применяться для практических расчетов, если известно фактическое значение коэффициента к, определенное экспериментальным путем или рассчитанное с помощью уравнения (111-57).
Мешалки, создающие радиально — осевой поток жидкости. Заданная радиальная модель потока жидкости может быть реализована только в случае некоторых типов турбинных мешалок. Мешалки многих других типов, например турбинные мешалки с наклонными лопатками, создают смешанный радиально-осевой поток. Для таких мешалок общий насосный эффект V* будет суммой радиального (V*pr) и осевого (F*2) потоков:
V*p = V*r+V*pz (II1-42)
Ван де Вуссе [216] для расчета насосного эффекта таких мешалок предложил метод, который может быть кратко охарактеризован следующим образом.
|
Со |
|
Ь 0-b)urcos<K |
|
Y’-kJarcos** |
|
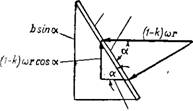
Рис. II1-23. Схема распределения вектора скорости для наклонной лопатки. |
|
Ъ — ширина лопатки; а — угол наклона лопатки относительно плоскости вращения; и = юг — окружная скорость лопатки. |
Лопатки мешалки наклонены относительно плоскости Z = const под углом а = const (этот угол не меняется с изменением радиуса г). Составляющие вектора скорости в радиальном и осевом направлениях показаны на рис. II1-23. Исходной для расчета отдельных составляющих скорости является разность (со — сос) г = (1 — k) cor между окружной скоростью мешалки и окружной скоростью жидкости, которая как тангенциальная скорость действует на лопатку в плоскости вращения мешалки, Z — const. Эту скорость можно разделить на составляющие: радиальную (1 — к) со г cos2 а и осевую (1 — к) со г sin A cos а. Поэтому насосный эффект радиального
потока для сечения окружности цилиндра Nbd и при условии, что (иг — Ndn, составит:
F*r = Jt2(l — К)Bud* cos2 a (111-43)
Насосный эффект осевого потока для поперечного сечения мешалки nd*l4 рассчитывают путем интегрирования, принимая элементарное поперечное сечение 2Nrdr И скорость уноса для радиуса о) = 2Ппг. Отсюда
D/2
F*2 = (1 — к) • 2лп sin a cos А • 2я | г* dr
О
После интегрирования имеем:
FpZ = sx2 (1 — /с) sin ос cos (III-44)
Суммируя уравнения (III-43) и (III-44), находим:
— ^cos2ct — f-Sin ot cos cc^j (III-45)
Принимая а = 45° и B = D/6, получаем:
F; = 1,64^3(1-/с) (II1-46)
Считая к = 0, имеем:
Мешалки, Создающие осевой поток жидкости. К таким мешалкам относятся главным образом пропеллерные. Насосный эффект здесь равен осевому потоку = V*Pz. По рекомендациям Ван де Вуссе [216] его можно рассчитывать аналогично тому, как это делается в случае наклонных лопаток. Однако при этом следует учитывать изменение угла наклона лопатки а. Пропеллерные мешалки чаще всего изготавливаются с радиально постоянным шагом. Тогда угол наклона пропеллера будет изменяться в соответствии с зависимостью
Которую можно преобразовать [163] до вида:
(ш-48> 9ТТ г
С. пя а. — —■=— ^ (Е ГI-49)
V $2 + 2л2г2
Насосный эффект для поперечного сечения Nd2/4 рассчитывают путем интегрирования зависимости:
D/2 О
|
Sin сц- |
8* 115
Б результате интегрирования получаем: Принимая Sid — 1 и к — О, находим:
V*
* Р=0.6
Nd 3
 29 ноября, 2012
29 ноября, 2012  admin
admin 
 Опубликовано в рубрике
Опубликовано в рубрике 