До сих пор было опубликовано лишь незначительное число уравнений, описывающих распределения скоростей жидкости в аппаратах с мешалками. Наибольшее количество данных по этому вопросу относится к аппаратам без перегородок и для тангенциальной составляющей.
При перемешивании жидкости в сосуде без перегородок мешалками с прямыми лопатками и для Re ;> 104 распределение скорости является приближенно симметричным по отношению к оси z, причем составляющая Wt не меняется вдоль высоты Z (рис. III-2). Таким образом, эта составляющая становится функцией только одного параметра Wt = / (г).
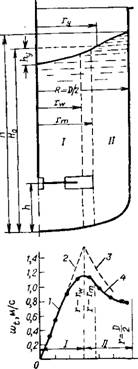
Многие авторы [1, 3, 67, 68, 131, 149, 163] считали, что в описанном выше процессе образуется вертикальный цилиндрический вихрь радиусом rw, называемый также центральным вихрем, и что поэтому весь объем жидкости в аппарате с мешалкой можно разделить на две зоны (рис. III-8):
1) цилиндрическая зона I в диапазоне 0 << г <lrw, в которой движение жидкости является вихревым, причем жидкость вращается с постоянной угловой скоростью сос; для этой зоны справедливо уравнение
Wt — G)cr (III-4)
2) цилиндрическая зона II в диапазоне Rw С R (называемая зоной невихревого или потенциального движения), в которой ско
рость снижается с увеличением радиуса по гиперболической1 зависимости:
|
(III-6) |
|
0,08 QJ6 024 0J2 Q40 0,48 Г/м |
|
Рис. II1-8. Схема возникновения центрального вихря: |
Wt = Cjr (Ш-5)
Только вблизи стенки скорость wt резко падает до нуля. Величины сос и С для данной системы определяются опытным путем. Для прямых лопаток, расположенных радиально, (ос (о = 2Яп. В качестве Rw принимается радиус, соответствующий максимальному значению Wt.
Мельников [131 ] первый определил приближенное значение радиуса центрального вихря Rw 0,75Гт. Применив воду в качестве перемешиваемой жидкости, он установил, что эта величина не зависит от числа оборотов мешалки.
Влияние геометрических параметров аппарата с мешалкой и физических параметров жидкости на значение Rw исследовали Аиба [1,3], Нагата и др. [143, 145, 148] и Гзовский [67, 68].
Аиба установил, что величина Rw явно зависит от вязкости жидкости и не зависит от высоты расположения и числа оборотов мешалки.
|
1 — уравнение (III-9); 2 — Уравнение (III-4); 3 — уравнение (III-5); 4 — уравнение (III-10). На основании та- |
Нагата и его сотрудники предложили для расчета радиуса Rw следующую зависимость:
Re
103+1,6 Re
Особенно широко исследовали эту проблему Гзовский и др. [67, 68], а также Карасев и Гзовский [95, 96]. Гзовский подтвердил наличие центрального вихря на основании измерений скорости растворения образца из твердой щавелевой кислоты, уложенного на дно сосуда. Оказалось, что наиболее интенсивное растворение образца наблюдалось на окружности радиусом г, ких измерений автор вывел формулу:
Rw „ 1
|
R 2 |
|
1 + — |
|
(III-7) |
|
Вт)1′ |
|
46 |
|
2rai +0,544 |
— = еХР"2"
|
97 |
1 Для таких условий свободная поверхность жидкости в зоне I представляет параболоид вращения, а в зоне II — гиперболоид вращения.
7 Заказ 1259
Здесь г у — радиус вихря на линии статического уровня жидкости (рис. III-8), рассчитываемый но зависимости
-iJL =0,508+ 0,215 ————— 0,3) (II1-8)
А пх — так называемое число источников и стоков (для нормального расположения мешалки принимается п1 = 4).
Согласно более новым исследованиям уравнение (Ш-7) дает завышенные значения, особенно для небольших значений критерия Рейнольдса.
Кроме радиуса центрального вихря Гзовский исследовал форму свободной поверхности жидкости, принимая, что она однозначно характеризует гидродинамическое состояние жидкости в аппарате с мешалкой и мощность, расходуемую на перемешивание. На основе более поздних исследований, выполненных в лаборатории Лен — НИИХиммаша [163], было, однако, доказано, что мешалки одного и того же диаметра, но разной конструкции, вызывают при одной и той же мощности, расходуемой на перемешивание, различную деформацию свободной поверхности жидкости (образуется воронка разной глубины).
Гзовский также провел интересные опыты. На вал мешалки он поместил металлический цилиндр диаметром 2rw (действительным для данных условий перемешивания), заменяя им цилиндрический вихрь, и придал ему вращательное движение вместе с мешалкой. Оказалось, что в форме свободной поверхности жидкости и в величине мощности, расходуемой на перемешивание, не произошло никаких изменений. Отсюда автор сделал вывод, что жидкость в области центрального вихря циркулирует только внутри этого объема.
В более поздних исследованиях Чепура и др. [38] показали, что описанная выше модель центрального вихря теоретически не обоснована и может рассматриваться лишь как приближенный метод для описания скорости Wt. Уравнения (Ш-4) и (III-5), как известно из гидромеханики [5], описывают так называемый классический вихрь Ренкина, для которого характерен резкий переход от вихревого движения к безвихревому, вследствие чего на границе этих двух видов движения производная Dwjdr претерпевает разрыв, что не согласуется с уравнением Ньютона.
Экспериментальные данные многих авторов [69, 131, 132] показывают, что вблизи г = Rw уравнения (III-4) и (111-5) завышают значения wt на 20—45%. Введение переходной зоны (рис. 111-8), предлагаемое некоторыми авторами [69, 131, 132], не вносит удовлетворительной поправки в точность этих уравнений. Желая убедиться в том, что движение в зоне II действительно является безвихревым (потенциальным), авторы работы [38] проверили значение скорости циркуляции Г и ротор вектора скорости гоTzw, рассчитывая эти величины с помощью формул:
Г = 2лгг^ (II1-9)
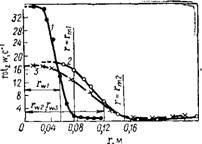
Для потенциального движения должно быть Г = const, rotZw = = 0. Как следует из рис. III-9 и 111-10, это не так. Для г >> Rw величина Г продолжает возрастать, rot2H> Ф 0, и лишь при г — гт можно говорить о практическом исчезновении завихренности движения. Поэтому авторы [38 ] принимают rot2^ = 0 только для г = гт и аппроксимируют зависимости rot2u> = f(r) параболой, откуда получают уравнение для расчета тангенциальной скорости: для 0 С г т
Для Rm < г < R
(I11-12)
Кгт 2г
Где к — (Dwtldr)R=O означает наклон кривой для г = 0, который должен быть определен опытным путем.
|
0,20 0J4 |
|
Рис. III-10. Результаты измерения функции rot2 W [38]. |
|
7* |
|
99 |
S6
|
О 0,041 0,08 012 0,16 0,20 0,24- OJ28 0J2 Г, м Рис. II1-9. Результаты измерения скорости циркуляции [38]. |
Относительно радиальной компоненты многие исследователи [1, 82, 148, 181] утверждают, что производная скорости Wr на! расстоя — ние г от центра аппарата с мешалкой является постоянной величиной, Wrr = const.
Карасев и Гзовский [96] установили экспериментально, что в аппарате без перегородок и с мешалками, лопатки которых расположены радиально, отношение радиальной и тангенциальной составляющих скорости является постоянной величиной, не зависящей от радиуса. Для исследованных ими аппаратов они вывели зависимость:
ШЧ^гГ
Где Аид — постоянные, зависящие от вязкости перемешиваемой жидкости; rja, — вязкость воды; 7 — угол между касательной, проведенной к линии потока, и нормалью к радиусу в рассматриваемой точке горизонтальной плоскости вращения мешалки.
Для л = 1-Ю"3—9-10-2 Па-с (1—90 сП) величина А = 0,535— — т-0,844, а Ъ = 0,69-^0,42.
Важной проблемой является также распределение скорости Wr По высоте лопатки, поскольку эта величина может служить для
определения насосного эффекта мешалки. Нагата и др. [146—148], Сакс и Раштои [181] и Каттер [37] приводят данные по этому вопросу. Максимальная скорость Wr наблюдается в плоскости, проходящей через центр мешалки (см. рис. II1-3 и II1-6). Сакс и Раштои [181] определили для открытой турбинной мешалки с четырьмя плоскими лопатками отношение средней скорости wr к максимальной скорости с для области, включающей высоту мешалки, Wr!Wr = = 0,64-М),81.
|
Г макс |
|
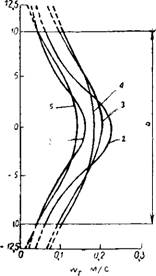
Значения г (вмм): 1 —50,8;2 — 67,8; 3 — 84,5; 4 — 101,0; 5 — 118,8. |
Авторы показали, что симплекс
Не зависит от скорости вращения мешалки, но возрастает с увеличением радиуса г. Значение 0,64 справедливо для концов лопаток, когда rlrfn = 1, а 0,81— когда г/гт — 2,33 при размерах D — 50,8 мм и D — = 406,4 мм в аппарате с перегородками.
Те же авторы установили, что скорость wr пропорциональна числу оборотов мешалки п. На рис. III-11 приведено примерное распределение скорости Wr в плоскости мешалки по данным этих авторов для различных радиусов г и при постоянном числе оборотов п = 100 об/мин.
|
|
|
Wr/w |
|
Рис. III-11. Распределение радиальных скоростей Wr В плоскости вращения мешалки при постоянном числе оборотов п = 100 об/мин; аппарат с отражательными перегородками [181]. |
Бласинский и Тычковский [19] исследовали распределение результирующей скорости в плоскости мешалки (плоскость перпендикулярна к оси аппарата и проходит через центр лопаток мешалки) в аппарате диаметром D = 700 мм без перегородок и с открытыми турбинными мешалками, имеющими шесть прямых лопаток различных диаметров. Авторы меняли геометрические параметры HID И D/D. Они вывели формулу для расчета результирующей скорости в плоскости мешалки
|
1,62 D |
|
0,223r-i. se ^ |
|
W Nd |
|
(111-14) |
Для области D/D — [15]/7^-1/2 и установили, что скорость вращения мешалки и высота ее установки при H/D = 1/3^-1/2 не влияют на значение отношения Iv/Nd.
Костин и Павлушенко [106] предложили формулу для результирующей скорости жидкости в аппарате с мешалкой. Авторы получили общее уравнение, пользуясь методом анализа размерностей, и затем проверили его для случая пропеллерной мешалки. Новые
Формулы для вычисления составляющих скорости Wz, Wr, Wt дает также в своей работе Демьянова [42].
Приведенные обобщения распределения скорости относятся в основном к аппаратам без перегородок и только к некоторым типам мешалок. Для аппаратов с перегородками обобщений пока не существует.
 29 ноября, 2012
29 ноября, 2012  admin
admin 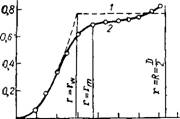
 Опубликовано в рубрике
Опубликовано в рубрике 