В качестве примера наиболее часто используемых формул для расчета массоотдачи можно привести зависимость:
GA=±kcF(CA-CAz) (VI-15)
Где GA — поток диффундирующей массы компонента А; кс — коэффициент массоотдачи, F — межфазная поверхность; СА — концентрация компонента А в ядре фазы; CAz — концентрация компонента
А на межфазной поверхности (индекс «z» означает межфазную поверхность).
Единицы измерения коэффициента теплоотдачи зависят от единиц измерения остальных величин в уравнении (VI-15). Чаще всего применяются следующие единицы измерения: С а — кмоль А/м3, F — м[32], GA — кмоль/ч; тогда коэффициент массоотдачи измеряется в м/ч. Знак «плюс» перед коэффициентом массоотдачи кс в уравнении (VI-15) означает, что массообмен происходит в направлении от ядра фазы к межфазной поверхности, а знак «минус», что направление массо — обмена — обратное, т. е. от межфазной поверхности к ядру фазы.
Если движущая сила процесса рассчитывается по мольным долям ха, то уравнение (VI-15) принимает вид:
GA= ±kxF(xA-xAz) (VI-16)
Где ха, Xaz — концентрации компонента А в ядре фазы и на межфазной поверхности соответственно, кмоль А/кмоль.
В таком случае при сохранении прежних единиц измерения GA и F коэффициент массоотдачи кх измеряется в кмоль/(м2-ч).
В литературе приводится ряд других уравнений массоотдачи с коэффициентами ку, ку, кр и т. д., единицы измерения которых различны
Для упрощения дальнейших рассуждений в этом разделе, а особенно для вычисления коэффициентов массопередачи, примем общие символы, выражающие концентрацию компонента А в двухфазной системе: для определения концентрации компонента А в фазе 1 — символ ZАч в фазе 2 — символ SА, не уточняя единицу измерения этих концентраций и не сообщая также, о какой фазе идет речь.2 При таких обозначениях уравнения массоотдачи для отдельных фаз двухфазной системы имеют вид:
GA = kZF(ZA-ZAz) (VI-17)
GA=kSF (SAz~SA) (VI-18)
Где Kz — коэффициент массоотдачи для фазы Z; Ks — коэффициент массоотдачи для фазы S;
Пригодность приведенных выше уравнений ограничена, так как В наиболее общем случае концентрации ZAz и SAz на межфазной поверхности неизвестны. Известно только, что эти концентрации должны быть равновесными друг другу. Используя равновесную кривую, их следует исключить посредством сложения диффузионных сопротивлений. Однако это сложение не такое простое, как в случае теплопередачи, где по обе стороны преграды движущей силой процесса
была разность температур, выраженная в одних и тех же единицах измерения. В процессе массопередачи единицы измерения концентрации фазы Z не равны единицам измерения концентрации фазы S, несмотря на то, что они могут иметь одинаковую размерность. Ввиду этого нужно сделать пересчет этих единиц измерения при использовании равновесных условий. С этой целью принимается, что в состоянии равновесия концентрация диффундирующей массы равна нулю, а отсюда концентрации в обеих фазах, выраженные в равновесных единицах, должны быть одинаковы, чтобы движущая сила процесса была равна нулю.
|
Г
|
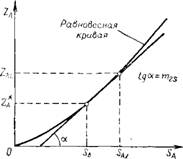
Рис. VI-3. Сложение диффузионных Рис. VI-4. Определение равновесных сопротивлений массоотдаче. концентраций при сложении диффу
Зионных сопротивлений массоотдаче.
Если график равновесия в рассматриваемом диапазоне концентраций может быть приближенно представлен прямой линией, описываемой уравнением Z*A — MZsSА + В, то нетрудно заменить концентрацию одной фазы на концентрацию другой фазы. Например, можно написать:
ZAz~ZA — mZS (SAz~ SA)
|
|
Где mzs — наклон равновесной линии в диапазоне концентраций Saz — SA; Z*A — концентрация компонента А, равновесная концентрации SА; ZAz, SAz — равновесные концентрации на межфазной поверхности (рис. VI-3 и VI-4).
После подстановки приведенной выше зависимости в уравнение (VI-18) и сложения левых и правых частей уравнений (VI-17) и (VI-18) получается:
ZS А
KzF ‘ ksF ZA~ZA
-F{ZK-Z) (VI-19)
ZS
Kz ks
Коэффициент массопередачи определяется выражением:
|
1 |
|
|
|
К, |
|
Z |
(VI-20)
|
(VI-21) |
Тогда уравнение (VI-19) можно записать короче:
Ga—KZF (ZA-Z1)
В приведенном выше уравнении коэффициент массопередачи был отнесен к концентрациям фазы Z (движущая сила процесса — разность концентраций фазы Z), отсюда дополнительное обозначение kz.
Величина Z*A является равновесной концентрацией компонента А, которая соответствует концентрации SА в фазе S. В качестве движущей силы процесса можно также использовать концентрации фазы S. По этой причине производятся замены
|
|
После подстановки этого выражения в уравнение (VI-17) и сложения левых и правых частей уравнений (VI-17) и (VI-18) получается:
|
|
|
Где |
(VI-22)
(VI-23)
Величина SА является равновесной концентрацией компонента А, которая соответствует концентрации Z& в фазе Z.
Коэффициенты массопередачи имеют в общем те же единицы измерения, что и коэффициенты массоотдачи для данной фазы, разность концентраций которой используется как движущая сила процесса. Таким образом, одинаковые единицы измерения имеют следующие величины: kz, Kz, ks и Ks•
Наиболее часто встречающиеся единицы измерения традиционных коэффициентов массоотдачи и массопередачи приведены в табл. VI-1. Это, разумеется, не все возможные единицы их измерения, а только важнейшие. Такое разнообразие единиц измерения этих коэффициентов затрудняет исследование проблемы и даже может быть причиной численных ошибок. К принципиальному упорядочению этих вопросов приводит только применение обобщенных характеристик диффузионных процессов, рассматриваемых в следующем разделе.
Таблица VI-1
Наиболее часто употребляемые единицы измерения традиционных коэффициентов массоотдачи и массопередачи
|
Aza, asa |
Обозначение коэффициентов массо |
Единицы измерения коэффициентов массоотдачи и массопередачи |
|
|
Отдачи и массопередачи |
Ga, кмоль/ч |
Ga, кг/ч |
|
|
ДСА, кмоль А/м3 |
Кс, К с |
М/ч |
— |
|
ДСА, кг А/м3 |
Кс, К-с |
— |
М/ч |
|
ДуА, кмоль А/кмоль Ах^, кмоль А/кмоль |
Ку, К у кх, Кх |
Кмоль/(м2 — ч) |
— |
|
ДуА, кг А/кг Дж^, кг А/кг |
Ку, Ку кх, Кх |
— |
Кг/(м2 • ч) |
|
ДрА, Па |
Кр, Кр |
Кмоль/(м2-ч-Па) |
Кг/(м2-ч Па) |
 30 ноября, 2012
30 ноября, 2012  admin
admin 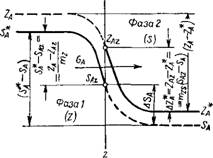
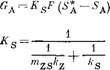
 Опубликовано в рубрике
Опубликовано в рубрике 