|
|
|
Рис. VI-2. График СА ~~ СА0 |
|
Функции Y |
|
= / (т, х) для неустано- |
|
С, |
|
‘А ^АО Вившейся диффузии, иллюстрирующий проникновение компонента А к элементу жидкости. |
Согласно этой теории, впервые предложенной Хигби [18], при интерпретации массопередачи от газа к жидкости межфазная поверхность не является статической (неизменной) величиной, а складывается на стороне жидкости
Из элементов, каждый из которых находится в контакте с газовой фазой только в течение короткого, но одинакового периода времени, после чего проникает в глубь жидкой фазы. Его место занимает новый элемент, прибывший из ядра жидкой фазы. Следовательно, на стороне жидкости нет постоянной ламинарной пленки, а турбулентность жидкости распространяется до самой межфазной поверхности. Таким образом, перенос массы осуществляется путем неустановившейся молекулярной диффузии от межфазной поверхности к элементу жидкости во время контакта т. Этот процесс описывается дифференциальным уравнением неустановившейся диффузии:
|
Дх* |
|
Дх |
(VI-3)
Где т — время диффузии; DА — коэффициент диффузии; х — расстояние от межфазной поверхности.
|
1) для я = 0 2) Для х= оо 3) для х Т> О |
Предположим, что концентрация компонента А для элемента жидкости на межфазной поверхности (Caz ) и в большом отдалении от этой поверхности (Сао) являются постоянными (рис. VI-2), что вполне допустимо ввиду короткого периода контакта. Тогда уравнение (VI-3) будет иметь следующие граничные условия:
Т^О Сд = С(равновесная концентрация) т^О СА = СА0
Т=0 (начальная концентрация)
Для решения уравнения (VI-3) выгоднее будет преобразовать его используя новую переменную
‘АО
|
Y = |
|
Az~ |
СА0
Тогда получим:
(УХ А ОХ 2
Граничные условия при этом упростятся
1) для х = 0 х ^ О У = 1
2) для х = оо т^О У = 0
3) для х>0 т=0 Y— О
Уравнение (VI-4) обычно решается методом преобразований Лапласа. Для этого нужно произвести простое (одностороннее) преобразование Лапласа:
Оо
У — | У exp (— рх) Dx О
Где р — комплексная переменная. Подобным образом
Оо оо
QY f dY Г _
О
Поскольку для т = О Y — 0 (граничное условие 3).
Преобразование Лапласа не зависит от х, значит можно написать:
D*Y dW Дх* ^ дх%
Таким образом, преобразовав обе части уравнения (VI-4), получаем:
— dW
ИЛИ
‘ F=o
0>х2 D ^
Интеграл этого уравнения имеет вид:
Y = B! exp (х Yp/DA) + Вг exp (- х /P/DA)
Постоянные Вх и Вг рассчитываются, исходя из граничных условий:
Оо
|
Отсюда и |
1) ® = 0, Y= 1, exp (—px)dx=l/p
О
2) х= оо, У = О, У = О Bi = 0; B2 = i/p
Y=-LexР {-xyjfDl)
После проведения обратного преобразования Лап ласа имеем
X
Y — erfc
2 У DJ Где
‘ erfc р = ^ exp(-p2)dp
Является функцией погрешностей Гаусса.
Окончательно для элемента жидкости можно написать следующее уравнение распределения концентраций:
Оо
CAZ-CAO Л J 4J0AT/ 2Y DAX J
2 У Dax
Распределение концентраций в элементе жидкости, представленное приведенным выше уравнением, показано на рис. VI-2.
Интенсивность потока диффундирующей массы для равномоляр — ного процесса рассчитывается по уравнению Фика
дх /х=о
Причем производная DCJdx, входящая в состав этого уравнения, определяется из зависимости (VI-5):
|
££а Дх |
|
С ехр |
|
0 Az ° Ар YNDA X |
|
Az АО |
|
4 D |
|
VNDi |
|
А |
|
Зс=0 |
Таким образом, можно получить следующее уравнение:
Уравнение (VI-6) описывает мгновенный поток массы в момент времени т. Средняя величина этого потока в период проникновения (пенетрации) хе вычисляется по зависимости
1,
Dx
Т
О
Что после интегрирования дает:
GA==2F/~1^(CAZ-CA0) (VI-7)
Следовательно, согласно пенетрационной теории, скорость массоотдачи пропорциональна коэффициенту диффузии в степени V2- Ввиду этого показатель степени В при критерии Шмидта в упомянутом
критериальном уравнении должен быть тоже равен V 2 (В = V 2). В большинстве экспериментальных работ по массоотдаче на стороне сплошной фазы указывается на то, что показатель степени В при критерии Шмидта более близок к значению V2, чем к нулю. Это свидетельствует о том, что пенетрационная теория лучше аппроксимирует ход процесса, нежели теория двух пограничных пленок.
Пенетрационная теория Хигби была модифицирована Данквер — стом [10, И], который выдвинул гипотезу, что продолжительность контакта элементов поверхности раздела фаз с вихрями элемента сплошной фазы неодинакова для всех элементов этой поверхности и что средняя интенсивность потока диффундирующей массы зависит от распределения элементов на группы с разным временем контакта т (так называемые «возрастные группы»). Распределение времени контакта может быть выражено функцией:
Ф(т) = /ехр(— Fx) (VI-8)
Где J — доля поверхности, обновляемой в единицу времени.
Средняя скорость проникновения получается при суммировании мгновенных скоростей проникновения для отдельных возрастных групп:
ОО р——-
О
= ^/(са-сАО) |/ У ^7= ехр с— /Т) ^х
О
Или
GA = V^JF(CAz-CAo) (VI-9)
Постоянная / должна быть определена экспериментально.
Следовательно, согласно теории Данкверста, называемой также теорией обновления поверхности, существует подобная зависимость коэффициента массоотдачи от коэффициента диффузии. Данкверст применил свою теорию для расчета массообмена в процессе абсорбции, осложненной химической реакцией.
Кишиневский [32—36] расширил теорию Хигби, предположив, что массоотдача к элементарным вихрям происходит в результате молекулярной и турбулентной диффузии (соответствующие коэффициенты диффузии D а и DД). Поэтому в формулу (VI-7) Кишиневский ввел эффективный коэффициент диффузии:
Для проверки предложенной модели процесса автор провел измерения абсорбции двуокиси углерода водными растворами гидрата окиси натрия в аппарате с мешалкой (абсорбция на свободной поверхности жидкости) и определил значения коэффициента турбулентной диффузии DА при различных числах оборотов мешалки.
 30 ноября, 2012
30 ноября, 2012  admin
admin 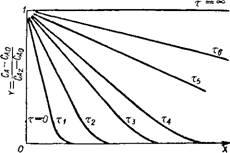
 Опубликовано в рубрике
Опубликовано в рубрике 