Под насосным эффектом мешалок следует понимать объемный расход жидкости через мешалку, рассматриваемую как ротор насоса. Математическое определение этой величины следует из баланса массового расхода для объема, описываемого вращающимися лопатками. Объемный расход жидкости через подразумеваемую таким образом контрольную поверхность при предположении, что плотность жидкости постоянна (7 = const), составит:
У* = JJ W+ cos сTdFx = J j W- cos adF2 (111-18)
Ft F.
Где W+, W~ — скорости жидкости, направленные наружу от объема, описываемого мешалкой, и внутрь этого объема; а — угол между вектором скорости и нормалью к контрольной поверхности в рассматриваемом месте; Fx, F2 — контрольные поверхности, через которые жидкость течет наружу и внутрь объема, описываемого мешалкой.
|
Рис. III-18. Схема циркуляции при наклоне и несимметричном расположении пропеллерной мешалки. |
Подставляя известные выражения для средних скоростей потоков в направлении, перпендикулярном к расчетной поверхности
|
Wx |
W+ cos adFx
|
Cos a.dF2 |
|
Ы>2 |
Я-
Уравнение (III-18) можно упростить до вида:
Vi = F1w1 = Ftfv2 (III-19)
Уравнение (III-19) принимает более наглядный вид для мешалок, создающих радиальный и осевой поток жидкости.
В первом случае контрольной поверхностью будет Fx = Ndb
(b — ширина _лоиатки мешалки), wx — средняя радиальная — скорость (w1 = wr), поэтому __
V*p = nbdwr (II1-20)
Средняя радиальная скорость должна быть рассчитана путем интегрирования распределения радиальной скорости для высоты Ь.
А
|
|
|
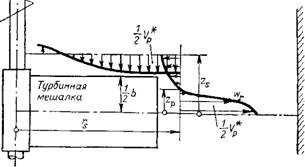
Рис. II1-19. Вспомогательная схема скоростей для вычисления насосного |
|
Распределения мешалки. |
Во втором случае F2 — лй2/4 и W2 = Wz (средняя осевая скорость в плоскости мешалки), отсюда
ТтЛ2 _
(II1-21)
Нагата, Ямамото и Уджихара [145] применяли для турбинных мешалок, создающих радиальный поток жидкости (рис. III-19), несколько модифицированное определение
Причем баланс расхода через мешалку должен замыкаться со стороны притока и стока, т. е. должна быть удовлетворена зависимость:
( сS
4лг, j" wrdz = 4лг8 J wrdz~B4^J wzdr
Приведенные выше формулы справедливы для случая, когда распределение скорости симметрично относительно плоскости вращения мешалки (отсюда в этих уравнениях множитель 4). Для других случаев интегрирование следует производить для верхней и нижней половины мешалок. Размеры цилиндра — радиус Rs и высота 2zs (рис. III-19) были выбраны произвольно, однако они не намного более радиуса Rm = D/2 и высоты лопатки Ъ. Это не должно повлиять na расчетное значение V*, поскольку, как следует из проведенных опытов [181], изменение wr с увеличением радиуса может быть выражено зависимостью (rwr)m ~ (rwr)s. Такие размеры расчетной поверхности облегчают использование опытных данных для Wr И wz1 которые труднее было бы измерить на кромках лопаток.
На рис. III-19 представлено распределение скорости Wr = F (г, Z) Для аппарата с мешалкой без перегородок, причем значение Wr — О достигается в пределах мешалки, отсюда Zp С. Ы2.
В случае аппарата с перегородками (рис. III-7) радиальная составляющая имеет положительное значение на всей высоте лопатки, тогда как радиальный поток жидкости выходит за пределы мешалки. Нагата и др. [148] предлагают в таком случае применять в уравнении (III-22) значение предела интегрирования, полученное для мешалок без перегородок. Другие авторы [181] принимали для расчета средней радиальной скорости wr значение радиального потока жидкости, умноженное на высоту лопатки Ъ. Это решение, кажется, является наиболее обоснованным. Ясно, что в данном случае насосный эффект меньше общего потока жидкости, отбрасываемого мешалкой в радиальном направлении.
 29 ноября, 2012
29 ноября, 2012  admin
admin 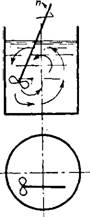
 Опубликовано в рубрике
Опубликовано в рубрике 