Если через аппарат непрерывно протекает жидкость, то в зависимости от интенсивности перемешивания в данном аппарате теоретически могут иметь место следующие случаи:
1) полное отсутствие перемешивания;
2) идеальное (полное) перемешивание;
3) неполное (частичное) перемешивание.
В первом случае частицы жидкости поступают п покидают аппарат, не перемешиваясь между собой. Это так называемый поршневой поток. Время пребывания каждой частицы жидкости в аппарате одинаково и равно времени протекания потока через аппарат. Такого рода поток в действительности не возникает в ньютоновских жидкостях вследствие молекулярной и вихревой диффузии, которые всегда приводят к некоторому продольному перемешиванию (в направлении течения потока). Во втором случае имеет место полное перемешивание, т. е. жидкость, поступающая в аппарат, очень быстро перемешивается с содержимым аппарата. Время пребывания отдельных частиц жидкости в аппарате различное и меняется от 0 до со. Такой процесс тоже является идеализированным и в действительности не имеет места, а может быть реализован лишь с некоторым
приближением. Практически во внимание можно принимать лишь третий случай.
|
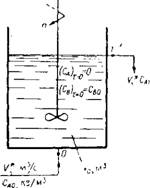
Рис. III-28. Схема, поясняющая материальный баланс аппарата проточного типа. |
В аппаратах непрерывного действия для перемешивания жидкостей представляет интерес распределение времени пребывания отдельных частиц жидкости [24, 44]. Это имеет важное значение, когда аппарат работает в качестве химического реактора. Проблемой распределения времени пребывания занимались многие исследователи. На первом месте здесь следует назвать работы Данквертса [41].
|
Рис. II1-29. Динамика перемешивания при течении жидкости через аппарат с мешалкой: |
1 — отсутствие перемешивания (поршневой поток);
2 — идеальное перемешивание; 3 — поршневой поток с некоторым продольным перемешиванием; 4 — неполное перемешивание.
Рассмотрим аппарат с мешалкой объемом V0 м3, через который непрерывно протекает жидкость В, плотностью С во кг/м3 в количестве V* м3/с. Величина
4 = V0/V* (III-70)
Называется средним временем пребывания частиц жидкости в аппарате. Если в определенный момент, который будет зарегистрирован как х = О, подаваемая жидкость будет заменена жидкостью А при том же расходе F* м3/с и с плотностью САО кг/м3 (рис. III-28), то можно оценить характер перемешивания измерением плотности компонента А на выходе из аппарата. В случае поршневого потока в период 0 <т <т на выходе из аппарата получим СА1 = 0, тогда как для т >т СА1 = СА0 (рис. III-29).
В случае идеального перемешивания плотность жидкости А на выходе из аппарата будет равна средней плотности в аппарате СА1 — СА и может быть вычислена из дифференциального уравнения материального баланса компонента А за период времени Dx При условии, что во время перемешивания происходит уменьшение объема:
(СА0~СА) F0 dCA (IH-71)
После интегрирования уравнения (111-71) и подстановки VJV* — т можно рассчитать распределение плотности компонента А в аппарате во время перемешивания
|
|
(111-72)
График функции (III-72) приведен на рис. III-29 (кривая 2). На этом же рисунке представлены графики для поршневого потока, частичного продольного перемешивания при поршневом потоке и неполного перемешивания, т. е. когда плотность жидкости в аппарате неодинакова.
По кривой распределения плотностей можно судить о времени пребывания частиц жидкости в аппарате. Например, в случае идеального перемешивания, частицы жидкости В, которые в момент т = 0 полностью заполняли аппарат, покидают его через различные отрезки времени в диапазоне от 0 до оо; следовательно, некоторые из них выходят из аппарата почти сразу же, а другие — через несколько часов.
Составив баланс массы тв компонента В, можно рассчитать, какая ее часть покинет сосуд спустя определенное время т.
|
Х |
Отсюда следует:
Х
|
|
(Ш-73)
Где 7?гво = V0Cm — общая масса компонента В, находящегося в аппарате в момент т = 0.
При допущении, что СА о = Сво = С а ~г С в — С, получим Св/Сво = [17] — (Са/Сао) или
|
|
(II1-74)
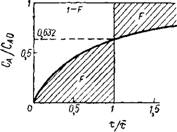
Приведенный выше интеграл представляет собой площадь на рис. III-30 между кривой распределения плотностей и прямой линией Сд/Сдо = 1 в диапазоне времени от 0 до т.
Для случая идеального перемешивания интеграл (111-74) может быть рассчитан, если принять значение [18] Атв/тв0 = 1 — е_т/т> т. е. форму уравнения (III-72). По истечении времени т = т величина Агпв/т-во = 1— (1/е) = 0,632; таким образом, только 63,2% частиц находится в аппарате меньше среднего времени пребывания.
Спустя бесконечно большое время % = оо вся масса жидкости В покинет аппарат, т. е. Аягв = т^о, поэтому
(111-7 5)
Из уравнения (III-75) следует, что общая площадь, заключенная между кривой распределения плотностей и прямой линией ^а/Сао = 1 всегда равна единице. Это видно на примере поршневого течения, где для т = f такая площадь достигает единицы. Для других случаев перемешивания характерное распределение площадей показано на рис. III-30.
|
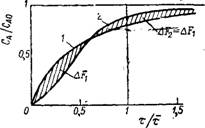
Рис. 111-31. Графическая интерпретация отклонения от идеального перемешивания по Данквертсу [41]: |
Идеального перемешивания; 2 Системы с сегрегацией.
Отклонение соответствующей кривой от линии идеального перемешивания является, по Данквертсу [41], мерой эффективности перемешивания системы (рис. Ш-31), или, иначе, величина площади AF = AFx + AF2 = 2 AF1 (равенство AF1 = AF 2 следует из идентичности площадей между любой кривой и прямой линией Са/Сао = 1).
Изложенные проблемы играют важную роль при проектировании химических реакторов, поскольку изменение распределения времени пребывания в реакторе отражается на протекании химической реакции.
|
Рис. II1-30. Графическая интерпретация уравнения (III-75). |
|
1 — для |
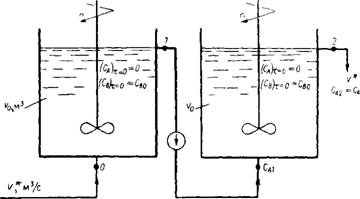
Как следует из анализа работы аппарата идеального смешения, распределение времени пребывания частиц жидкости является неблагоприятным. Одни частицы находятся в аппарате очень мало, другие — очень долго. Более однородное время пребывания достигается при наличии батареи последовательно установленных аппаратов. Для примера проведем для двух аппаратов с мешалками, работающих параллельно (рис. III-32), такой же расчет как и для одного аппарата, принимая, что в обоих аппаратах осуществляется идеальное перемешивание и они имеют тот же объем Vx — V2 = Потребуется вычислить плотность компонента А на выходе из батареи СА2 = СА.
Баланс по компоненту А для первого аппарата:
|
(II1-76) |
|
С |
С,
‘ А1
АО
Где т1 = У о/У* — среднее время пребывания в одном аппарате с мешалкой.
Для второго аппарата дифференциальное уравнение материального баланса имеет вид:
|
Рис. II1-32. Схема работы двух последовательно соединенных проточных аппаратов с мешалками. |
|
С„о, хг/м3 |
V* (CA1 — Cx)dx=VbdCk (IIJ-77)
После преобразования и подстановки У0/У* = тг имеем:
|
Ti |
DC, .
(II1-7?
Dx
Проинтегрировав уравнение (Ш-78), получим выражение для распределения плотности компонента А на выходе из второго аппарата с мешалкой:
|
С, |
|
1-4- |
|
С |
|
АО |
(Ш-79)
Подобные вычисления для батарей, состоящих из трех, четырех или п аппаратов с мешалками проводят по формуле:
АО
(111-80) 137
Если принять во внимание среднее время пребывания для всей батареи т = nV0/V* = пхх, то уравнение (III-80) будет иметь вид:
1 / пт 3 1 / гет
^зт(т) +-"+Т^1)т(т) J <1П"81)
Уравнения (II1-80) и (III-81) были выведены многими авторами [43, 47, 102, 124] различными способами. Графическое изображение уравнения (III-81) Приведено на рис. III-33. Как следует из этого рисунка, применение нескольких аппаратов с мешалками, соединенных последовательно, приближает течение жидкостей к поршневому режиму.
Преимуществом такого аппаратурного решения является возможность установления различных температур в отдельных аппаратах, что в свою очередь может оказаться полезным при проведении химической реакции. Использование аппаратов различных объемов позволяет получать различное время пребывания реагентов в соответствующих температурных зонах. Для этого случая Холанд и Чап — ман [81 ] вывели уравнения, позволяющие определить плотности СА2 и САЗ*
 29 ноября, 2012
29 ноября, 2012  admin
admin 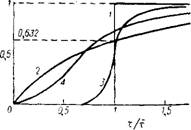
 Опубликовано в рубрике
Опубликовано в рубрике 