Лако-красочные материалы — производство

The tool of the one-factor Analysis of Variance (ANOVA), combined to the statistical test of Fisher (usually regarded as the F-test), is the most suitable methodology to state if a factor has an impact (i. e., a significant effect) on one or more response variables. In the present study the ANOVA was applied to process the experimental data, in order to establish if the ER has an effect on the adhesive strength and on the K ratio. For the sake of clarity the whole procedure is briefly summarized below, before reporting the results concerned with the present research. Full details are contained in Ref. [22] and related references. A preliminary step to the analysis consists in the rearrangement of the data to be processed in a two-dimensional array, where the columns refer to the factor levels, while the rows are related to replicated results. A general example is shown in Table A1, considering C levels for the involved factor and Rj replicated data for each level (the number of replicated data may be different, depending on the level).

Table A1. Sample table of the results to be processed

Let yj represent the result corresponding to the (j-th) level of the factor and to the (i-th) replication, and let y be the average of the data retrieved for

the (j-th) factor level, listed in the (j-th) column. The symbol y indicates the

Grand Mean over all the results. The total amount of variance in the experiment, usually regarded as Total Sum of Squares, TSS, can be computed as in Eq. (A1).

The TSS can be split into two terms: the first one accounts for the effect of the studied factor and is called Sum of Squares Between Columns, SSBC, whereas, the second one takes the experimental uncertainty into account and is regarded as the Sum of Squares Error, SSE. The related expressions are shown in Eqs. (A2) and (A3).

ssbc=ik — h., — yf ]

j=1

The question regarding the significance of the factor is tackled, comparing SSBC and SSE. For this purpose, these two terms must be properly scaled, i. e., divided by the related degrees of freedom, vSSBC and vSSE (see Eqs. (A4) and (A5)).

Vssbc= C -1 (A4)

^ssE=i(^j -1) (A5)

j=1

The scaling procedure leads to the computation of the Mean Squares, MSBC and MSE, as in Eqs. (A6) and (A7).

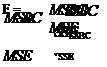The following step consists in the computation of the Fisher ratio, Fcaic, i. e., the ratio between MSBC and MSE.

Finally, the p-value, p-v., is computed as a function of Fcala, vssbc and vsse, considering the Fisher distribution of the Fisher ratio. This outcome leads to the F-test, where the p-v. is compared to a significance level a. The final response is that the factor has a significant impact on the output, if p-v.< a. Otherwise, it is concluded that the output is not significantly affected by the factor. The level a is usually assumed as 5%, as suggested in many References, such as [22].

Analyses of variance were performed to compare the results in terms of the adhesive shear strength rad and of the ratio K for different values of ERs, varying in the range from 0.4 to 1.7 (4 levels as a total). The analyses processed both the results of the first campaign on HJs (Tables A2-A3) and those retrieved in the second campaign (Tables A4-A5), in order to investigate the effect of ER at different interference levels.

Table A2. ANOVA and Fisher test regarding the impact of ER on rad
(first campaign on HJs)

Table A3. ANOVA and Fisher test regarding the impact of ER on K1
(first campaign on HJs)

Table A4. ANOVA and Fisher test regarding the impact of ER on zad
(second campaign on HJs)

Table A5. ANOVA and Fisher test regarding the impact of ER on K1
(second campaign on HJs)

Acknowledgments

The Authors would like to gratefully acknowledge Profs. Matteo Mozzini and Stefano Ruggeri and all the students of the “Scuola Specializzata Superiore di Tecnica” in Bellinzona (Switzerland) for their kind support in the manufacturing of shaft and hub specimens. The Authors also acknowledge Eng. Paolo Proli, Director of the DIN Mechanical and Aerospace Lab, for his help in the experimental part of this research.