Силы, действующие между двумя телами в дисперсиях, обычно называют поверхностными силами. Они обусловлены не только атомами на поверхности вещества, но и атомами, находящимися в его объеме. Гамакер [19] рассчитал эти силы. Их можно представить следующим образом:
Va= — А/АЫ [l/d*+l/(d+ 6)2-2/(d+j^j J; (5.6)
Если d»6, то VA=— 6M/32jxd4; (5.6а)
D< 6 VA=-A/4&n[l/d2-7/b2]-, (5.66)
D< б VA=—A/4&nd (5.6в)
У________ энергия притяжения для двух пластин толщиной б на расстоянии друг
От друга равном 2d; А — константа Гамакера для вещества, из которого состоят пластины.
Гамакер [20] также показал, что энергия притяжения (V.,) между двумя одинаковыми сферами радиуса а, расстояние. между поверхностями которых d, равна:
Кд= —Л/6 [2/(S2 — 4) +2/S2 + ln{(S2 — 4) /S2)], (5.7)
Где S = 2 + d/a.
Если d<Ђ. a, то
Vk~—Aa/I2d, (5.7а) •
И для сфер с радиусами щ, а2:
V — Асца? (5 76)
А &d (ai +а2)
Можно рассчитать силы притяжения, зная размер частиц, среду, расстояние между ними, и выразить результаты в виде энергии притяжения (VA). Однако константа Гамакера А получена для вакуума. При рассмотрении энергии притяжения между двумя частицами в жидкости необходимо ее модифицировать с учетом окружающей среды. Гамакер показал, что частицы вещества А і в среде вещества Ач имеют общую константу Гамакера A—Ai-j-A2 — 2-/ЛЙ2. Если имеются два разных вещества-— 1 и 2 в среде 3, то модифицированная константа Гамакера равна:
AI32=(A(2-AU2)(AM2-AW). (5.8)
‘ Перечень значений констант Гамакера для обычных веществ дан в работе [21]. Грегори [22] показал, как на основании простых экспериментальных измерений можно приблизительно рассчитать константу Гамакера.
.Следует обратить внимание на то, что эти силы всегда являются силами притяжения. При необходимости получения большей точности можно вводить поправки, например уточнение Волда с учетом адсорбционных слоев [22] или Казимира и Полдера с учетом запаздывания сил притяжения. [24, 25]. Но простое рассмотрение опубликованных значений констант Гамакера показывает, что они могут изменяться на порядок и поэтому редко оправдана необходимость использования усложняющих поправок с целью учета непостоянных трудно уловимых эффектов, таких как в работах Волда [23] и Винсента [26].
Хотя между двумя одинаковыми частицами всегда действует сила притяжения, Виссер [27] отмечает, что при определенных условиях можно получить отрицательную константу Гамакера в трехкомпонентной системе, когда Аи С ЛззС^гг или Ац >Лзз > >-<422, где Лзз представляет собой индивидуальную константу Гамакера данной среды. Важно отметить, что и в этом случае одинаковые частицы Ац, находящиеся в среде Л33, также как
И А-22 в среде Лзз по-прежнему будут притягиваться, но частицы А п и Л22 — отталкиваться друг от друга. Примером подобного типа отсутствия ассоциации, как полагают, могут быть частицы политетрафторэтилена и графита в воде.
Чтобы получить «коллоидную дисперсию» необходимо создать условия, чтобы энергия отталкивания (Vr) между частицами была больше энергии притяжения и в результате сложения этих двух энергий оставалась бы значительная результирующая энергия отталкивания. Поскольку энергии отталкивания и притяжения зависят от расстояния между частицами, важно знать распределение частиц, особенно в красках, которые с коллоидной точки зрения рассматриваются как «концентрированные» системы. Можно показать, что в случае плотной упаковки сферических частиц, отношение расстояний между поверхностями частиц (5) к расстоянию между центрами частиц (с) связано с общим объемом зависимостью:
____________________________ S/c=] — (ОКП/0,74) ‘/3, _ (5.9)
Где ОКП — объемная концентрация пигмента,
Ниже приведены значения ОКП и расстояния между поверхностями сферических частиц:
Г* с ОКП S/d ОКП S/d
30 0,35
35 0,28
40 0,23
45 0,18
Для монодисперсных сферических частиц любого размера среднее расстояние 5 равно одному диаметру частицы при ОКП равном 9,25%. Поэтому среднее расстояние между частицами для ТЮг при такой концентрации равно приблизительно 200 нм, а для меньших частиц при той же ОКП это расстояние будет пропорционально меньше.
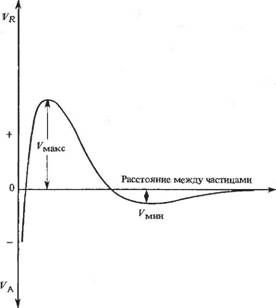
Если сравнить энергии отталкивания и притяжения, помня, что для частиц, находящихся в Броуновском движении, средняя энергия перемещений при комнатной температуре равна 3/2 kT, то для их стабилизации необходимо иметь энергетический барьер (^макс), значительно превышающий эту величину (рис. 5.3).
|
|
На кривой общей энергии может наблюдаться «вторичный минимум», соответствующий энергии, которая характеризует возможность существования слабой флокуляции. Она называется «слабой флокуляцией» (1/мин) или «вторичной минимальной флокуляцией» в отличие от более сильной флокуляции, которая происходит при дальнейшем сближении частиц и иногда называется «первичной флокуляцией». Следует заметить, что иногда в литературе [28] пользуются терминологией, отличной
|
Рис. 5.3. Типичная зависимость общей энергии от расстояния между частицами, показывающая наличие «вторичного минимума» (V„„„ флокуляции) |
От используемой в лакокрасочной промышленности; например, термин «коагуляция» в литературе употребляется для описания флокуляции, в то время как обычно этот термин в промышленности применяют тогда, когда наблюдается необратимая ассоциация латексных или эмульсионных частиц.
 11 июля, 2012
11 июля, 2012  admin
admin 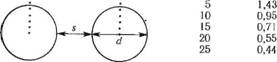
 Опубликовано в рубрике
Опубликовано в рубрике 