Опыт показал, что наряду с изотермами адсорбции, вид которых показан на рис. IV, 1, довольно часто на практике встречаются изотермы, не имеющие второго участка, почти параллельного оси давлений и отвечающего насыщению поверхности адсорбента молекулами адсорбтива. Вид таких изотерм изображен на рис. IV, 5. Как можно видеть, в точке А изотерма Ленгмюра круто поднимается кверху. Очевидно, связывание адсорбтива адсорбентом не прекращается после образования мономолекулярного слоя, а продолжается дальше. Форму подобных изотерм нельзя объяснить
|
|
|
Рис. IV, 5. Вид изотермы, характерной для полимолекуляр- иой адсорбции. |
|
Рис. IV, 6. Схема адсорбционного объема по представлениям полимолекулярной теории адсорбции. |
|
А |
Как следствие капиллярной конденсации, так как такая изотерма наблюдается и у непористых адсорбентов, когда капиллярная конденсация невозможна.
Для объяснения этого явления Поляни в 1915 г. предложил теорию полимолекулярной адсорбции, называемую также потенциальной. Рассмотрим кратко исходные положения этой теории, особенно пригодной в случае адсорбции паров на твердом теле.
1. Адсорбция обусловливается чисто физическими силами.
2. На поверхности адсорбента нет активных центров, а адсорбционные силы действуют вблизи от поверхности адсорбента и образуют около этой поверхности со стороны газовой фазы непрерывное силовое поле.
3 Адсорбционные силы действуют на сравнительно большие расстояния, во всяком случае большие, чем размеры отдельных молекул адсорбтива, и поэтому можно говорить о существовании У поверхности адсорбента адсорбционного объема, который заполняется при адсорбции молекулами адсорбтива.
4. Действие адсорбционных сил по мере удаления от поверхности уменьшается и на некотором расстоянии практически стано — вится равным нулю.
5. Притяжение данной молекулы поверхностью адсорбента не зависит от наличия в адсорбционном пространстве других молекул, вследствие чего возможна полимолекулярная адсорбция.
6. Адсорбционные силы не зависят от температуры, и, следовательно, с изменением температуры адсорбционный объем не изменяется Это не противоречит тому, что с повышением температуры адсорбция уменьшается; в этом случае снижение адсорбции обусловливается не уменьшением адсорбционных сил, а увеличением в результате нагревания интенсивности теплового движения адсорбированных молекул, что приводит к увеличению десорбции.
Из рассмотрения положений теории полимолекулярной адсорбции можно видеть, что силовое поле, возникающее у поверхности адсорбента, во многом сходно с гравитационным полем (ненасыщаемость поля молекулами адсорбтива, находящимися непосредственно на поверхности адсорбента; независимость сил, действующих в поле, от температуры).
На рис. IV, 6 схематически показан разрез адсорбционного объема, отвечающий представлению теории полимолекулярной адсорбции. Как и во всяком силовом поле, в адсорбционном поле можно представить себе эквипотенциальные поверхности, т е. поверхности с одним и тем же адсорбционным потенциалом. На рисунке они обозначены пунктирными линиями. Под адсорбционным потенциалом 0 следует понимать работу, совершаемую против адсорбционных сил при перемещении 1 моля адсорбтива (пара) из данный точки поля в газовую фазу. Очевидно, максимальный адсорбционный потенциал должен существовать на границе адсорбент — адсорбционный объем. На границе адсорбционный объем — газовая фаза, т. е. там, где кончается действие адсорбционных сил, потенциал 0 должен быть равным нулю.
Изменение адсорбционного потенциала обычно выражаетсн в теории полимолекулярной адсорбции не как функция расстояния I от поверхности адсорбента, а как функция адсорбционного объема V. Это обусловлено тем, что функция 0 = /(V) экспериментально сравнительно легко определяется, в то время как нахождение функции 0 = F(L) вызывает подчас иеопреодолимые трудности В самом деле, адсорбционный объем легко иайти, если работа ведется, например, при достаточно низких температурах Тогда адсорбтив находится в Адсорбционном пространстве в виде жидкости. В этом случае заполненный жидкостью адсорбционный объем Уж, отвечающий 1 г адсорбента, выражается следующим уравнением
Уж = вКмол (IV, 14)
Где а — количество адсорбтива (в молях), адсорбированного I г адсорбента; Умол — мольный объем конденсата.
Толщину слоя жидкости в адсорбционном объеме можио было бы иайтя по уравнению-
U^VJs (IV, 15)
Где 5 — поверхность адсорбента
К сожалению, из-за сложности определения истиииой поверхности адсорбента эту величину часто очень трудно определить, поэтому Поляни и предложил выражать 0 ие как функцию /, а как функцию пропорциональной величины V.
Изменение адсорбционного потенциала 0 с изменением адсорбционного объема V, как это представлял Поляни, показано на рис. IV, 7. Подобные кривые, не зависящие от температуры и характерные для каждого данного адсорбента, Поляни называет характеристическими кривыми.
Теория полимолекулярной адсорбции принимает, что для адсорбционного объема применимо уравнение состояния газа. Поэтому изотермы, характеризующие зависимость плотности адсорбтива р от адсорбционного объема V для разных температур, напоминают йзотермы р, V.
В определенных условиях, например при достаточно низкой температуре, адсорбционные силы на поверхности могут вызвать конденсацию пара в жидкость плотностью рж. При температурах значительно более низких, чем критическая, в результате конденсации весь адсорбционный объем будет заполнен жидкостью, так что Vm = УМакс — В этом. случае кривая р = f(V) на участке, 1 соответствующем адсорбционному © объему, идет почти параллельно оси абсцисс в связи с малой сжимаемостью жидкости. Далее на границе адсорбционный объем — газовая фаза кривая резко опускается вниз И плот — Рис. IV, 7. Типичный вид ха — ность адсорбтива достигает значения рактеристической кривой, плотности газовой фазы ро.
При температурах значительно более высоких, чем критическая, адсорбтив будет вести себя как идеальный газ и график зависимости Р ОТ 7 выразится Кривой, СХОДНОЙ с изотермой ДЛ5Ґ идеального газа PV = RT. В этом случае адсорбированный газ будет обладать максимальной плотностью у поверхности адсорбента, минимальной — в непосредственной близости от газовой фазы. Плотность адсорбтива в адсорбционном объеме здесь нигде не достигает плотности жидкости.
Наконец, когда температура близка к критической, зависимость р от V выразится, очевидно, кривой, близкой по своему виду К изотерме, описываемой уравнением Ван-дер-Ваальса. В этом случае часть адсорбированного вещества будет находиться в адсорбционном’объеме в жидком состоянии, а часть—в газообразном. Понятно, наиболее резко кривая снижается в участке, отвечающем переходу от жидкости к газу.
Исходя из приведенных выше представлений, Поляни указал путь для построения характеристической кривой. Потенциал 0і, отвечающий точке і, находящейся на поверхности раздела жидкость — га» в адсорбционном объеме, мож» но представить как работу сжатия 1 моля газа при температуре Т;
Pi
Є(= ^V dp (IV, 16)
|
|
Р>
Где р, — давление насыщенного пара над поверхностью жидкости, р0 — давление газа в газовой фазе
Так как V = RT/P, значение 0І можно вычислить по уравнению:
Pi Pi d
В» — ^V dp — RT ^ — RT In (IV,17)
Po P-
Значение pt для большинства веществ известно; значение р0 определяется из опыта. Для нанесения соответствующей точки на диаграмму, выражающую зависимость адсорбционного потенциала от адсорбционного объема, неооходимо знать, какому значению V, соответствует найденное значение 0,. Для этого пользуются вышеприведенным уравнением (IV, 14).
Определив V, и 0, для ряда значений р0 при температуре значительно более низкой, чем критическая, когда адсорбтив находится в адсорбционном объеме в основном в виде жидкости, можно построить график 0 = F(V). Наличие в правой части уравнения (IV, 17) множителя Т не указывает на то, что зависимость 0, от Vг должна меняться с температурой; а лишь показывает, что при другой температуре, но при том же значении р0 адсорбционный потенциал, соответствующий границе жидкость — газ, будет иным
М М. Дубинин показал, что потенциальная теория адсорбции дает возможность вычислить изотермы адсорбции различных паров на одном и том же адсорбенте по характеристической кривой, полученной из изотерм адсорбции одного пара, так как соотношение адсорбционных потенциалов различных паров практически не зависит от адсорбционного объема. Из этого следует, что координаты точек характеристических кривых для разных адсорбтивов в случае одного и того же адсорбента при всех значениях адсорбционного объема находятся в постоянном отношении р, т. е. эти кривые являются афинными. Отношение р называется коэффициентом афинности характеристических кривых. Отсюда следует, что построив характеристическую кривую по экспериментальной изотерме адсорбции одного адсорбтива и зная соответствующий коэффициент афинности для какого-нибудь другого адсорбтива, можно найти изотерму адсорбции для этого второго адсорбтива.
Мы рассмотрели кратко две теории адсорбции — теорию мономолекулярной адсорбции Ленгмюра и теорию полимолекулярной адсорбции Поляни, на первый взгляд исключающие друг друга. Возникает вопрос, какая из этих теорий более правильна? На это следует ответить, что обе теории ограничены в применении. В зависимости от природы адсорбента и адсорбтива и в особенности от условий адсорбции в одних случаях приложима одна, а в других— другая теория адсорбции. Теория Поляни применима только к явлениям чисто физической адсорбции. Теория Ленгмюра охватывает с известными ограничениями явления как физической, так и химической адсорбции. Однако теория Ленгмюра не может быть применена для объяснения адсорбции на тонкопористых адсорбен* тах, имеющих сужающиеся поры. В местах сужения, вследствие аддитивности дисперсионных сил, адсорбционный потенциал более высок и в таких местах происходит более интенсивная адсорбция. Это особенно заметно при температурах ниже критической температуры адсорбтива, т. е. при адсорбции паров, которые в этом случае заполняют наиболее узкие места капилляров в виде жидкости. Применение уравнения Ленгмюра к адсорбции тонкопористыми адсорбентами, имеющими поры с сужениями, затруднительно. Конечно, формально, уравнением Ленгмюра можно описать
адсорбцию такими адсорбентами. Однако константа йМакС в этом случае теряет смысл емкости плотного монослоя, и использование Этой константы для определения удельной поверхности таких адсорбентов уже не дает правильных результатов.
Делались попытки обобщить представления Ленгмюра и Поляни и описать изотермы различной формы с помощью одного уравнения. В частности, такая обобщенная теория была развита Брунауэром, Эмметом и Теллером в 1935—1940 гг. применительно к адсорбции паров. Их теория получила название теории БЭТ по первым буквам имен авторов. Основные положения теории БЭТ следующие.
1. На поверхности адсорбента имеется определенное число равноценных в энергетическом отношении активных центров, способных удерживать молекулы адсорбтива.
|
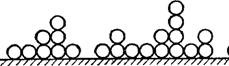
Рис. IV, 8. Схема полимолекуляриой адсорбции, принятая по теории БЭТ. |
|
|
|
77/ г. |
2. Для упрощения взаимодействием соседних адсорбированных молекул в первом и последующих слоях пренебрегают.
Оба эти допущения соответствуют ленгмюровской адсорбции на однородной поверхности без взаимодействия адсорбированных молекул.
3. Каждая молекула первого слоя представляет собой возможный центр для адсорбции и образования второго адсорбционного слоя; каждая молекула второго слоя является возможным центром адсорбции в третьем и т. д.
4. Предполагается, что все молекулы во втором и более далеких слоях имеют такую же сумму статистических состояний, как в жидком состоянии (в общем отличающуюся от суммы состояний первого слоя).
Таким образом, адсорбированная фаза может быть представлена как совокупность адсорбционных комплексов — молекулярных цепочек, начинающихся молекулами первого слоя, непосредственно связанных с поверхностью адсорбента. При этом цепочки энергетически не взаимодействуют друг с другом. Схема строения адсорбционного слоя по теории БЭТ показана на рис. IV, 8.
|
97 |
Все эти предпосылки достаточно условны. В частности, согласно теории БЭТ принимается, что каждая молекула жидкости имеет только двух ближних соседей (т. е. сверху и снизу в цепочке), в то время как у молекулы реальной жидкости гораздо больше ближайших соседей. Тем не менее эта теория оказалась в некоторых отношениях весьма плодотворной.
4 Зак, 664
Теория Поляни не позволяет вывести уравнения изотермы адсорбции. Теория БЭТ, как и теория Ленгмюра, дает аналитическое уравнение для изотермы, которая в этом случае имеет S-образную форму (см. рис. IV, 5). Не приводя достаточно сложного вывода уравнения изотермы адсорбции Брунауэра, Эммета и Теллера, остановимся лишь на некоторых положениях, лежащих в основе этого вывода, и приведем само уравнение изотермы.
Брунауэр, Эммет и Теллер при выводе уравнения рассматривают адсорбцию молекул пара как серию квазихимических реакций образования единичных и кратных адсорбционных комплексов:
Пар + свободная поверхность единичные комплексы пар + единичные комплексы двойные комплексы пар + двойные комплексы тройные комплексы и т. д.
При этом теплота адсорбции первого слоя молекул Qi, т. е. теплота образования единичных комплексов, гораздо больше, чем для всех последующих слоев. Теплоты адсорбции всех последующих слоев приблизительно одинаковы и равны теплоте объемной конденсации L.
Для константы равновесия полимолекулярной адсорбции С можно написать следующее уравнение:
C = g’exp(-Јi—-) (IV, 18)
(Qi — L)—так называемая чистая теплота адсорбции
На основе этих представлений Брунауэр, Эммет и Теллер вывели следующие уравнения изотермы адсорбции паров:
|
(IV, 19) (IV, 20) |
„_____________ «макс С pips_________
О-/»//».) П +(C-)Plps]
__________ "макс Cp/ps_________
(1 — P! Ps)[ +(С- )Ptps]
Где Ps — давление насыщенного пара при данной температуре, P/Ps — относительное давление пара, ос, аМакс, а, амако, р — имеют те же значения, что и в уравнении Ленгмюра
При значениях р, далеких от и С > 1, адсорбция приводит к образованию мономолекулярного слоя и уравнения (IV, 19) и (IV, 20) переходят в уравнения адсорбции Ленгмюра (IV, 10) и (IV, 11). По мере приближения р к Ps число свободных активных Центров сокращается и кратность комплексов растет. При р = р„ происходит объемная конденсация пара.
Уравнение изотермы полимолекулярной адсорбции БЭТ легко привести к линейной форме
А (і —PPips) = ^Ьс + *plps (IV>21)
По наклону этой линии и отсекаемому ею отрезку на оси ординат можно найти значения констант амакс и С.
Теория БЭТ, так же как и теория Ленгмюра, указывает путь для определения удельной поверхности адсорбента. Найдя амАкс для паров простых веществ (N2, Аг, Кг) при низких температурах и зная площадь So, занимаемую молекулой адсорбтива, легко вычислить удельную поверхность адсорбента syA:
^уд^макс^О <IV>22)
Где NA — число Авогадро.
Легко решить и обратную задачу. Для этого определяют с помощью адсорбции при низких температурах стандартного пара поверхность s-уд данного адсорбента, после чего, найдя экспериментально изотерму адсорбции пара исследуемого адсорбтива и значение емкости монослоя амакс, вычисляют значение S0:
Опыты по определению удельной поверхности одного и того же адсорбента при адсорбции различных паров дали близкие результаты, в общем совпадающие с результатами определения удельной поверхности другими, не адсорбционными методами. Это подтверждает правильность толкования формы изотермы с помощью теории БЭТ. Несмотря на ряд недостатков, теория БЭТ является в настоящее время лучшей и наиболее полезной теорией физической адсорбции.
 1 ноября, 2012
1 ноября, 2012  admin
admin 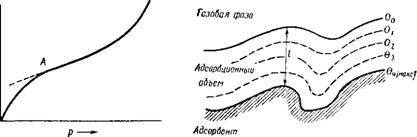

 Опубликовано в рубрике
Опубликовано в рубрике 