Различают адсорбцию газа на твердом теле, адсорбцию растворенного вещества на границе раствор — газ и, наконец, адсорбцию растворенного вещества на границе твердое тело — раствор.
Адсорбция газа на твердом теле является простейшим случаем адсорбции, так как система газ — твердое тело состоит всего из двух компонентов. Поэтому адсорбция газа твердым телом особенно удобна для теоретического рассмотрения явления адсорбции.
Имеется несколько теорий физической адсорбции, из которых рассмотрим прежде всего теорию мономолекулярной адсорбции. Теория эта была предложена в 1915 г. американским ученым Ленгмюром, но, как отмечает сам Ленгмюр, им использованы представления об адсорбционных силах, впервые выдвинутые русским ученым Л. Г. Гурвичем.
При разработке теории Ленгмюр исходил из следующих положений.
1. Адсорбция является локализованной и вызывается силами, близкими к химическим. Однако следует отметить, что Ленгмюр считал химическими все силы, обуславливающие когезионную прочность вещества, а также проявляющиеся в явлениях испарения, кристаллизации, поверхностного натяжения и т. д.
2. Адсорбция молекул адсорбтива происходит на активных: центрах, всегда существующих на поверхности адсорбента. Такими центрами могут быть пики и возвышения, имеющиеся на любой, даже самой гладкой поверхности. Так, на поверхности кристаллов известкового шпата имеются выступы высотой в 10~4—Ю-5 см, даже тонко отполированные зеркала имеют на поверхности выступы до 3- Ю-7 см.
В результате большой ненасыщенности силового поля около таких шгкбв~и выступов эти участки обладают способностью удерживать налетающие молекулы газа, причем центр тем более активен, чем ненасыщеннее молекулы адсорбента на его поверхности.
Примером поверхности с центрами различной активности может служить поверхность восстановленного никеля, для которой Тейлор дает следующую схему строения:
I
—Ni—
I I I
—Ni— —Ni— —Ni—
II II I II
—Ni—Ni— —Ni—Ni— —Ni— —Ni—Ni—
I I I I I I I I I I I
—Ni—Ni—Ni—Ni—Ni—Ni—Ni—Ni—Ni—Ni—Ni—
I I I I I I I 1 I 1 I
—N i—N i—Ni—N i—Ni—N i—N i—N i—N i—N i—N i—
I I I I I I I I I I I
Атомы никеля, связанные с поверхностным слоем одной связью, благодаря большой ненасыщенности адсорбируют молекулы адсорбтива сильнее или в большем количестве, чем атомы никеля, связанные с поверхностью двумя связями. В свою очередь, на последних адсорбция проходит интенсивнее, чем на атомах никеля, связанных с поверхностью большим числом связей.
Ряд исследователей считает также, что активными центрами являются ребра и углы кристаллов и границы зерен в микронеоднородном или,-как говорят, микрогетерогенном адсорбенте, около которых образуются особенно интенсивные силовые поля. То, что ребра и углы кристаллов обладают повышенной способностью адсорбировать молекулы адсорбтива, можно показать на следующем примере. Если поместить кристалл медного купороса в спиртовый раствор сероводорода, то почернение кристалла из-за образования сульфида меди всегда начинается с углов и ребер.
Обычно принимают, что активные центры занимают лишь незначительную часть поверхности адсорбента. Эту точку зрения подтверждает то обстоятельство, что количество яда, отравляющего катализатор, как правило, гораздо меньше того количества, Которое потребовалось бы для покрытия ядом всей адсорбционной поверхности.
3. Вследствие малого радиуса действия адсорбционных сил, имеющих природу, близкую к химической, и способности их к насыщению каждый активный центр, адсорбируя молекулу адсорбтива, становится уже неспособным к дальнейшей адсорбции. В результате этого на поверхности адсорбента может образоваться только мономолекулярный слой адсорбтива.
4. Адсорбированные молекулы удерживаются активными центрами только в течение определенного промежутка времени. Через некоторое время, в результате флуктуации кинетической энергии, молекулы отрываются от поверхности адсорбента и переходят в газовую фазу. Взамен этих молекул активные центры могут адсорбировать новые молекулы, которые в свою очередь десорби — руются, и т. д.
Время пребывания молекулы в адсорбированном состоянии на активном центре в значительной степени зависит от температуры. При низких температурах это время может быть очень большим. При высоких температурах порядка 1000—2000 °С время пребывания молекулы в адсорбированном состоянии может равняться всего миллионным долям секунды.
5. Ленгмюр не учитывал силы взаимодействия между адсорбированными молекулами. Другими словами, согласно Ленгмюру, время пребывания молекул газа на активных центрах не зависит от того, Заняты молекулами газа соседние активные центры или нет.
Исходя из приведенных выше положений, Ленгмюр смог дать общее уравнение изотермы локализованной адсорбции, пригодное как для описания адсорбции газов, так и растворенных веществ.
Для вывода этого уравнения применительно к адсорбции газа представим локализованную адсорбцию как квазихимическую реакцию между молекулой газа и активным центром адсорбента, в результате которой образуется адсорбционный комплекс, т. е. молекула адсорбтива, адсорбированная адсорбентом: молекула газа + активный центр адсорбента <=±: адсорбционный комплекс
Согласно этой реакции и принимая во внимание, что число молекул газа, ударяющихся о поверхность адсорбента, пропорционально давлению газа, можно написать:
А = Kpa0 (IV, 6)
Где а — поверхностная концентрация адсорбтива; осо — концентрация свободных активных центров на поверхности адсорбента; р — давление газа; K — константа, не зависящая от концентрации и постоянная при данной температуре.
При установившемся адсорбционном равновесии:
K = a/(pa„)
В этом єлучае K является константой равновесия.
Принимая во внимание, что каждый активный центр может быть занят одной молекулой, можно написать:
А + а0 = аМакс (IV, 7)
Где амакс — поверхностная концентрация адсорбтива при заполнении им всех активных центров.
Уравнение (IV, 7) можно переписать в виде:
Ао — «макс — О (IV, 8)
Подставим это уравнение в уравнение (IV, 6):
А = Kp (а„акс — а) (IV. 9)
Решая уравнение (IV, 9) относительно ос, получим:
A=aM3KCkpf(+kp) (IV, 10)
Это и есть уравнение изотермы адсорбции Ленгмюра. Иногда уравнение Ленгмюра пишут в несколько ином виде;
АмаксР _ АмаксР — I/к + р А + р
Где А — величина, обратная константе равновесия. «
Поскольку величина адсорбции а пропорциональна ос, уравнение Ленгмюра можно представить и в таком виде:
А = аМакс*р/(1 + Кр) = аМЗксрК А + р) (IV, 11)
В этом уравнении аМакс — количество адсорбтива (в молях), адсорбированное единицей массы адсорбента (1 г), соответствующее полному заполнению всех активных центров. Таким образом, в уравнении Ленгмюра обе константы осМакс (или амАьс) и K имеют определенный физический смысл.
Уравнение Ленгмюра хорошо описывает изотерму адсорбции, давая при малых и больших значениях р приблизительно прямолинейные участки на графике, чего не дает уравнение Фрейндлиха.
В самом деле, при малых давлениях в знаменателе уравнения (IV, И) можнб пренебречь членом Kp, весьма малым по сравнению с единицей, и уравнение Ленгмюра принимает вид, тождественный с уравнением Генри, которому подчиняется распределение вещества между двумя фазами: а = амакс kp = Kp. Таким образом, при малых р адсорбированное количество вещества прямо пропорционально равновесному давлению. Этот случай соответствует начальному почти прямолинейному участку изотермы. При больших значениях р в знаменателе уравнения Ленгмюра можно, наоборот, пренебречь единицей, и тогда уравнение примет вид а == Ямакс, т. е. адсорбированное количество вещества перестает зависеть от давления, что отвечает относительно прямолинейному участку изотермы, идущему почти параллельно оси давлений.
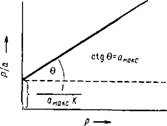
Для графического решения ураинение Ленгмюра приводят к виду:
——— Х—г + —— (IV, 12)
А вмаксй Дмакс
Полученное уравнение есть уравнение прямой в координатах р/а и р. Наглядно 0 видно из рис. IV, 3. Очевидно, аМАкс = ctg 0, где 8 — угол наклона прямой
к абсциссе, а 1/(амакД)—отрезок, отсекаемый прямой на оси ординат. Зная l/(aMaitcft) И а макс, легко вычислить k[5]
Как известно, константа равновесия K всякой химической реакции связана с теплотой реакции Q уравнением
K = ge^/RT (IV, 13)
Где G — постоянный множитель
Так как при физической адсорбции всегда выделяется тепло, т е Q > 0, то из уравнения (IV, 13) следует, что с ростом температуры константа равновесия должна уменьшаться Это происходит из-за увеличения кинетической энергии молекул и возрастания вследствие этого десорбции Отсюда становится понятным, почему адсорбция газов при высоких температурах и не слишком высоких давлениях незначительна, а предел адсорбции в этих условиях не достигается (см рис IV, 1)
|
|
Уравнение изотермы адсорбции Ленгмюра хорошо приложимо, «ели адсорбция вызывается силами, близкими по своей природе
|
|
Рис. IV, 3. Решение уравнения Рис. IV, 4. Изотерма ступен-
Ленгмюра путем его преобра — чатой .адсорбции,
Зования в уравнение прямой.
"к химическим силам, и если адсорбция не осложняется рядом побочных явлений, например диссоциацией молекул адсорбированного газа на поверхности.
Представления, развитые Ленгмюром, позволяют объяснить так называемую ступенчатую адсорбцию. В этом случае изотерма адсорбции носит своеобразный ступенчатый характер, как показано на рис. IV, 4. Это явление легко объяснить, если допустить, что на поверхности адсорбента существуют группы активных центров, резко отличающиеся по активности. Первая ступень изотермы, очевидно, отвечает заполнению группы наиболее активных центров, происходящему уже при малых давлениях, вторая — заполнению группы активных центров с меньшей активностью, что требует ■более высоких давлений и т. д.
Однако некоторые случаи физической адсорбции не могут быть объяснены положениями теории мономолекулярной адсорбции и требуют принципиально иного подхода с позиций полимолекулярной адсорбции.
 1 ноября, 2012
1 ноября, 2012  admin
admin 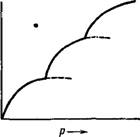
 Опубликовано в рубрике
Опубликовано в рубрике 