Диффузией называют самопроизвольно протекающий в системе процесс выравнивания концентрации*молекул, ионов или коллоид — Ййх — чгастиц род влиянием их теплового хаотического движения. Таким образом, диффузия является макроскопическим проявлением теплового движения молекул и поэтому всегда идет тем быстрее, чем выше температура. Явление диффузии необратимо, она протекает до полного выравнивания концентраций, так как хаотическому распределению частиц отвечает максимальная энтропия системы.
|
Рис. III, 2. Схема броуновского движения частицы. |
Част(^ за причину диффузии принимают осмотическое давление. Это представление было развито Нернстом (1885 г.). Так как осмотическое давление может проявляться лишь при наличии полупроницаемой перегородки (мембраны), то это давление бессмысленно рассматривать как какую-то реальную силу, суще
ствующую вне связи с мембраной. Тем не менее осмотическое давление, являющееся также результатом хаотического движения молекул, иногда действительно очень удобно принимать за причину диффузии. Правомерность такого подхода подтверждается соответствием теоретических данных, полученных, исходя из этоЛ точки зрения, с экспериментальными.
Перенос массы в результате диффузии формально сходен с закономерностями переноса тепла или электричества. Воспользовавшись такой аналогией, Фик (1855 г.) сформулировал первый закон диффузии:
Dm = — D~sdx (III, 2).
Где т — количество продиффундировавшего вещества; D — коэффициент диффузии, зависящий от свойств диффундирующих частиц и среды, dc/dx — градиент концентрации; 5 — площадь, через которую идет диффузия; т — продолжительность диффузии.
Знак минус перед правой частью равенства поставлен потому, что производная Dcldx имеет отрицательное значение, так как с увеличением значений х величина с уменьшается.
Уравнение (III, 2) можно представить также в виде:
, Ід = l/s (dm/dx) = — D dc/dx (III,3>
Величину ід принято называть удельным потоком диффузии, так как она характеризует количество вещества, переносимое в результате диффузии за единицу времени через сечение, равное единице площади. —
Диффузионный поток в общем случае является функцией от х и т, так как от этих величин зависит градиет концентрации Dc/Dx. Только если поддерживать градиент концентрации постоянным. Диффузионный поток не изменяется с течением времени и в системе устанавливается стационарный процесс диффузии. Для этого — случая, очевидно, можно написать:
Т = _ д-^- st (Ш,4>
«Принимая Dc/Dx = —1, S = 1 и т — 1, получим
D = M (111,5)-
Т. е. коэффициент диффузии D численно равен количеству вещества, продиффундировавшего через единицу площади в единицу времени при градиенте концентрации, равном единице. Из уравнения (111,4) также следует, что коэффициент диффузии измеряется в см2/с. Однако очень часто при рассмотрении явлений диффузии в связи с медленностью процесса за единицу времени берут не секунду, а сутки.
Эйнштейн (1908 г.) вывел уравнение, связывающее коэффициент диффузии D с абсолютной температурой системы Т, вязкостью дисперсионной среды т) и радиусом частиц дисперсной
фазы г. Для вывода этого уравнения, имеющего большое практическое и теоретическое значение, представим себе изображенную на рис. 111,3 трубку с сечением в S см2, заполненную раствором, причем примем, что концентрация растворенного вещества равномерно убывает слева направо. Выделим мысленно в этой трубке слой раствора бесконечно малой толщины, ограниченный воображаемыми плоскостями х{х[ и хОбъем этого элементарного слоя V будет равен Sdx. Обозначим концентрацию раствора и осмотическое давление слева от этого слоя через с — и щ, & справа от него — через с2 и л2. Очевидно, Сі > с2 и щ > л2. При
Таких условиях в трубке происходит диффузия растворенного вещества, причем перенос вещества будет идти слева направо, как указано на рисунке стрелкой. Как известно, диффузия обусловлена хаотическим тепловым движением частиц, когда частицы движутся в отдельные моменты с различной скоростью и в разных направле — Рис. 111,3. Схема, поясняющая ниях. Однако, рассматривая диффу — лывод уравнения Эйнштейна. зию в целом как направленный поток
Частиц, можно говорить о некоторой эффективной постоянной скорости. Такой скоростью должны обладать все частицы, чтобы, двигаясь прямолинейно, перенести через единицу сечения за единицу времени при данном градиенте концентрации определенное количество вещества.
Постоянная скорость диффундирующих частиц может быть объяснена тольког тем, что движущая сила /, действующая на отдельную частицу, уравновешивается обратно направленной силой трения испытываемой этой частицей, т. е. что
F = r (Пі. 6)
■Сила трения равна произведению коэффициента трения В между частицей и средой на скорость движения частицы и:
F‘ = Bu (III, 7)
Коэффициент В для сферических частиц равен по Стоксу бятг (где г) — динамическая вязкость среды и г — радиус частицы).
Для вычисления движущей силы, действующей на одну частицу, определим сначала движущую силу F, приходящуюся на •единицу объема элементарного слоя. Очевидно
Р__ — "і — ________________
Sdx sdx sdx
Тогда, если молярную концентрацию растворенного вещества в элементарном слое обозначить через с, то движущую силу F, прихо
дящуюся на одну частицу, можно представить следующим образом:
F_ Dn _ RT dc (iii 8)
‘ ScdxNA scN д dx
Где R— универсальная газовая постоянная; T — абсолютная температура; ЛГа — число Авогадро.
Вставляя найденные выражения для f и / в уравнение (111,6), лолучаем:
„ RT dc /IIT П.
Ви ———- -г—— -т- (пі, 9)
ScN д dx
Это уравнение можно переписать следующим образом:
RT dc _1_ Ис~ sMA‘ dx ‘ в
Но ис есть не что иное, как количество вещества пг, продиффун- дировавшее в единицу времени через единицу площади. Поэтому
~ ЯГ-*’-1 (111,10)
SMA dx В
Согласно уравнению Фика, для тех же условий
M = — D^t4 (111,11)
Приравнивая правые части уравнений (111,10) и (111,11), на-, ходим:
Это и есть уравнение Эйнштейна. Для частиц, по форме близких к сферическим, В = бяцг и
RT KT
^^’W^emr (Ш’,3)
Как можно видеть, коэффициент диффузии прямо пропорционален абсолютной температуре и обратно пропорционален вязкости среды и радиусу частиц. Поскольку размеры коллоидных частиц очень велики по сравнению с размерами обычных молекул, коэффициент диффузии в коллоидных системах мал.
Поэтому Грэм пришел в свое время к неправильному заключеНию, что диффузия в коллоидных системах отсутствует. ,, Пользуясь уравнением Эйнштейна, можно легко определить Массу 1 моля вещества, если известны значения D, Т и rj. В самом Пеле, из уравнения (III, 13) следует, что
R = kT/(6niD) (111,14)
Определив по уравнению (III, 14) радиус частиц, можно вычислить массу 1 моля вещества М:
М = 4ъпг3 pNA (ill, 15)
Где р — плотность дисперсной фазы, которая обычно известна.
Таким образом, измеряя коэффициент диффузии, можно определить молекулярный вес вещества (численно равный массе 1 моля вещества).
Перрен и Герцог на основании определения коэффициента диффузии в водных растворах вычисли пи молекулярные веса некоторых углеводов, допустии,- что молекулы их имеют сферическую форму и они настолько малы, что воду можно рассматривать как непрерывную среду и что увеличения радиуса молекул, а следовательно, и коэффициента В вследствие сольватации растворенного вещества не происходит. Полученные ими результаты приведены в табл. Ill, 1.
|
Таблица III. 1. Молекулярный вес разлччных углеводов, вычисленный по коэффвциенту диффузии
|
Совпадение экспериментальных результатов с рассчитанными на основании данных о химическом строении этих веществ достаточно удовлетворительно, несмотря на сделанные допущения.
Для экспериментального определения коэффициента диффузии предложено много методов. Все они основаны на том, что раствор диффундирующего вещества приводят в контакт T растворителем таким образом, чтобы между ними образовалась возможно более четкая граница раздела. Полученную систему выдерживают некоторое время при постоянной температуре в условиях, полностью’ исключающих сотрясения и тепловую конвекцию, и затем определяют наступившее в результате диффузии новое распределение концентрации растворенного вещества в системе. По полученный результатам, обычно с помощью специальных таблиц, вычисляют коэффициент диффузии.
Различные модификации этого способа отличаются только аппаратурным оформлением и способом определения распределения концентрации вещества после диффузии. Распределение концентрации может быть установлено с помощью осторожного отбора проб и их анализа, а также путем определения характера изменения окраски, абсорбции света или коэффициента преломления раствора по высоте столба жидкости. Экспериментальные методы
Определения коэффициента диффузии подробно описаны в руководствах к практическим занятиям по физической и коллоидной химии.
Причияа. _диффузи. и_.в ясіїшішх-растворах,-так выше указано, заключается в_ тепловом движении молекул. Аналогично jj коллоидных системах причиной диффузии дисперсной фазы является броуновское движение частиц. фс’ЛИ существует связь между броуновским движением и диффузией, то должна существовать связь между средним квадратичным значением проекции смещения частицы Д и коэффициентом диффузии D. п Эта связь была установлена Эйнштейном (1905 г.) и независимо от неге Смолуховским (1906 г.).
Для установления зависимости & = f(D) воспользуемся несколько упрощенными рассуждениями Эйнштейна, приведенными в одной из его работ. Ка. к и при выводе уравнения Эйнштейна, представим себе изображенную на рис. 111,4 трубку с поперечным се. чением в s см2, наполненную коллоидным раствором, концентрация которого равномерно уменьшается слева направо. В этом же направлении, конечно, будет идти и диффузия коллоидных частиц. Выделим мысленно в этой трубке два слоя раствора 1 и 2 со средними концентрациями растворенного вещества А и С2, отвечающими концентрации вещества в центре выделенных слоев. Пусть А — среднее квадратичное значение проекции смещения частицы на ось, параллельную направлению диффузии, за время т.
|
(III, 16) |
Вследствие хаотичности броуновского движения перенос любой частицы растворенного вещества равновероятен вправо и влево. Масса вещества, перенесенного за время т через воображаемую плоскость MN вправо, будет Rri = С As/2, а влево M2 = C2A.S/2. Очевидно, в результате обоих этих процессов количество вещества, продиффундировавшее через плоскость MN слева направо, выразится уравнением:
Т. — тх — M2 = V»ci ~ лк°2 = ~ сг) S
Но из рис. 111,4 следует, что
Подставив уравнение (111,18) в уравнение (111,16), получим:
Т=_-1д2_£Ё-s (Ш, 19)
2 dx
Объединяя уравнение (111,19) и уравнение Фика т — —Dsxds/Dx, Имеем: _
D = Д2/(2х) (111,20)
Или _
(Ш,21)
Из этого следует важный вывод, что величина А, а следовательно, и само смещение пропорциональны не т, а Vт-
Вставляя в уравнение (111,21) значение D из уравнения Эйнштейна (III, 13), можно получить:
^-VT^-VIF (ш’22)
Это уравнение обычно называют уравнением Эйнштейна — Смолу — ховского.
Сведберг пройерил правильность уравнения Эйнштейна — Смо — луховского, исследуя под ультрамикроскопом золи золота. Он определял значения Д через разные промежутки времени и вычислял теоретические значения А по формуле A = V&iT> где k = = йГ/(Зяг)г). Ниже приведены полученные им результаты для золя золота с частицами диаметром 0,044 мкм:
Время наблюдения, с……………………. s. 1 2 3 4
Значение Д, мкм
Экспериментальное…………………… 4,3 5,8 6,6 8,3
Вычисленное…………………………….. 4,1 5,8 7,6 8,2
Совпадение результатов оказалось вполне удовлетворительным. Подобные же результаты были получены Сведбергом на других объектах, а также и другими исследователями.
Помимо этого для проверки правильности уравнения Эйнштейна — Смолуховского Сведберг определял зависимость А от вязкости дисперсионной среды коллоидной системы. В этом случае для вычисления теоретического значения А он пользовался
Формулой A = V&3Al> гДе K2 = KTxl(Znr).
Наконец, Зеддиг проверил правильность уравнения Эйнштейна — Смолуховского, определяя зависимость А от температуры. При этом теоретические значения А он вычислял по уравнению А = д/ Дг3Г/т), где K3 = Kxj {Злг). В правой части этого равенства фигурирует величина rj, поскольку вязкость дисперсионной среды меняется с температурой. И в этом случае опыт подтвердил теорию.
Пользуясь уравнением Эйнштейна — Смолуховского и зная значение А и всех остальных величин, можно вычислить число Аво-
гадро. Это проделал Перрен, проводивший опыты с суспензией Гуммигута. Вычисленное им число Авогадро равнялось 6,8-1023, что близко к значениям NA, определенным другими методами
Интересно, что Перрен нашел значение числа Авогадро, наблюдая не только поступательное, но и вращательное движение микроскопически видимых частиц. Как было указано в предыдущем разделе, под влиянием ударов, сообщаемых частице молекулами среды, она начинает вращаться. Это вращательное движение, как показал Эйнштейн, подчиняется уравнению:
|
|
(iii, 23)
Где 0 — среднеквадратичное угловое смещение частицы за время т.
Перрен, наблюдая под микроскопом вращение относительно больших частиц суспензии мастики и пользуясь уравнением (111,23), получил для числа Авогадро значение, равное 6,5-1023.
Исследование броуновского движения и диффузии в коллоидных системах не только дало многое для понимания природы дисперсных систем и установления общности молекулярно-кинетиче — ских свойств этих систем и систем молекулярной дисперсности, но и явилось доказательством правильности молекулярно-кинетиче — ской теории в целом. Теория броуновского движения, созданная Эйнштейном и Смолуховским, подтвердила реальное существование молекул как раз в то время, когда по этому вопросу развернулась ожесточенная дискуссия, поднятая Вильгельмом Оствальдом и другими представителями энергетической школы, советовавшими избегать пользоваться понятиями атома и молекулы, поскольку, по их мнению, за этими словами не кроется объективная реальность.
Таким образом, значение теории броуновского движения выходит далеко за пределы коллоидной химии, в которой она, кстати говоря, явилась первой количественной теорией. Теория броуновского движения, согласно которой движение коллоидных частиц — прямое следствие теплового движения молекул, приобрела огромное значение в физической химии, физике и философии, явившись убедительным обоснованием правильности материалистического мировоззрения. Исследование броуновского движения привело к созданию теории флуктуаций и способствовало развитию статистической физики.
|
65 |
Флуктуации представляют собой спонтанные отклонения какого-нибудь параметра от среднего равновесного значения в достаточно малых объемах системы. Флуктуациям подвержены физические величины (например, плотность, концентрация), биологические (рост, продолжительность жизни), социально-экономические (плотность населения в данном месте, цена товара) ■И т. д. Основы общей теории флуктуаций заложены американским ученым Гиббсом (1902).
3 Зак 664
Простейшим способом наблюдения флуктуаций в коллоидной системе является определение через равные промежутки времени числа частиц, находящихся в микроскопически малом объеме. Например, при подсчете таким образом числа частиц, находящихся в 1000 мкм3 золотого золя, Сведбергом был получен следующий ряд значений: 1, 2, 0, 0, 2, 0, 0, 1, 3, 2, 4, 1, 1, 2, З, 1, 1, 1, 1, З, 1, 1, 2, 5, I, 1, 2, 3. Всего им было сделано 518 наблюдений. В среднем число частиц в выделенном объеме составило 1,545, но в отдельные моменты оно падало от 0 и повышалось до 7.
Несоответствие найденных чисел среднему значению можно объяснить только тем, что хаотическое движение частиц приводит к случайному попаданию в выделенный микрообъем то большего, то меньшего числа частиц. Понятно, что если бы вместо микрообъема был выделен для наблюдения достаточно большой объем, содержащий огромное число частиц, то в результате компенсации избытка частиц в одних его участках недостатком частиц в других участках средняя численная концентрация в таком макрообъеме оказалась бы постоянной.
Из сказанного следует, что флуктуации представляют собою явление как бы обратное явлению диффузии, хотя оба они обусловлены тепловым движением. При диффузии происходит выравнивание концентраций в макрообъемах, а флуктуации представляют собою спонтанное отклонение концентрации от среднего его значения в микрообъемах.
В нашем курсе мы не можем рассматривать теорию флуктуаций. Отметим лишь, что применительно к коллоидным системам эта теория позволяет вычислить вероятность различных численных концентраций в микрообъемах, а также найти тот промежуток времени, через который данная концентрация снова повторится в выделенном объеме. Это время обычно весьма резко возрастает с увеличением отклонения концентрации от среднего значения. Так, расчеты показывают, что в 1 мл газа при нормальных условиях отклонение численной концентрации на 1% может произойти через 10180 лет, т. е. практически невозможно Однако абсолютной невозможности осуществления подобного события все же нет, что характерно для второго начала термодинамики, носящего статистический характер.
 1 ноября, 2012
1 ноября, 2012  admin
admin 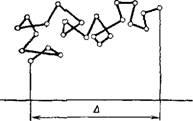
 Опубликовано в рубрике
Опубликовано в рубрике 