Деформирование материала также может быть описано в первую очередь усилием и смещением, а не напряжением и деформацией — Излишне говорить, что полученные в результате испытаний данные в одинаковой степени зависят как от типа образца, так и от его механических свойств. Такой тип зависимости используют для анализа результатов испытания при расслаивании, показанною на рис. 2.3. В гл. 1 рассматривались образцы материала, имеющие дефект в виде полости и без него, и появляющиеся в зависимости от вида образца различия в концентрации напря женин. Механика разрушения описывает способность материала сопротивляться влиянию концентрации напряжении (дефекту), существующему внутри образца. Как показано на рис. 2.з. .что положение справедливо при использовании образца, имеющею неопределенные размер и форму, по известную ширину.
Где-то внутри его го тела имеется трещина с острыми краями (аналогичная торцевой трещине, представленной на рис. 2.3, и полости, показанной на рис. 1.1) Трещина имеет длину а. К телу прикладывается усилие, в результате чего появляется смешение. Исли принять, что тело является линейным II упругим, ТО кривая «напряжение деформация* будет аналогична первому участку кривой, показанной на рис. 2.6 (тонкая сплошная линия). 11ри таком состоянии рассчитывают плотность энергии деформации. Используя обозначения, приведенные на рис. 2 6, можно получить:
Ї/, — (/■,/),)/2. (2-9)
Это уравнен не просто описывает плоишь иол тонкой сплошной линией парне — 2 6.1? определенной точке во время деформирования тела трещина и нем растет. Когда это происходит, изменяется жесткость тела и проявляется новая кривая «напряжение деформация». І Іаклои кривой «напряжение лс<|юрмаііпя» изменяетс я, гак как жесткость тела становится отличной от исходного состояния в результате того, что тело теперь имеет трещину большего размера. Таким же образом рассчитывается плот-
|
F А
|
F
Рис. 2.5. Схематические изображение тела неопределенных размеров, нгпольаоианного для описания элементарной механики линейно-упругого разрушения. Тело имеет неопределенную форму, но известную ширину а1. Где-то внутри тела имеется трещина длиной и. Усилие /’может быть приложено к телу, что приводит к смещению Г)
|
|
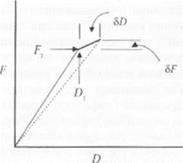
Рис 2.6. Кривая «напряжение деформация» для линейно-упругого тела, нр< -дета влек ного на рис. 2.5. Следует заметить, что обе кривые, соответствующие нагруженному (тонкая сплошная линия) н нснагру жен ному (пунктирная линия) состояниям идентичны Наклон кривых объясняется изменением жесткости тела при распространении трещины. Показанный более толстой линией участок кривой соответствует изменению угла наклона кривой нагружения в результате распространения трещины. Обозначения, представленные на рисунке, рассматриваются ниже
шкть энергии деформации Г, и теле после распространения трещины. Она представляет собой площадь иод более толстой сплошной линией. Так как материал янляется линейным и упругим, можно рассчитать плотность оперши деформации по уравнению:
(/, — Ftbl) + (№0)/2. (2.10)
Определит ь эту характеристику также довольно просто. Площадь под более толстой сплошной линией определяется небольшим треугольником, площадь которо
го составляет (л/ЪГ))/2. и параллелограммом, площадь которого составляет FfiD. Кривая для ненагружснного образца должна отвечать пунктирной линии участка кривой. Плотность энергии деформации U для этого участка кривой описывается уравнением:
(2.11)
Это выражение представляет собой площадь треугольника, находящуюся под пунктирным участком кривой. Параметры U. и V.: описывают энергию, приложенную к образцу и приводящую его в конечное состояние. Однако это состояние образца не соответствует сто исходному состоянию, так как в данном случае в материале произошло разрушение в результате появления трешииы. И данном случае нужно принимать во внимание различие между энергией, приложенной к образцу, и энергией, которую мог бы воспринимать образец в непогруженном состоянии. Энергия U, приводящая к распространению трещины, выражается в виде:
![]() (2.12)
(2.12)
Данный аналитический метод описывает энергетический подход к распространению трещины, но не является критерием для оценки энергии, необходимой для развития такой трещины. Величина деформации известна, когда определенное напряжение приложено к линейно-упругому материалу, В этом случае необходимо знать характеристику материала, способствующую раснросгранению трещины, аналогичную модулю Юнга при испытании на растяжение. Предположим, что трещина распространяется только втом случае, когда Ut > 0тт. Значения U, и U т < имеют размерность энергии и нс связаны с размером образца и завершившимся ростом трещины. Как показано на рис. 2.5, ширина образца составляет и. В момент роста трещины бесконечно малая величина изменения действующей энергии по сравнению с изменением длины трещины должна превышать минимальную энергию, необходимую для роста трешнны. Если отнести эту величину к ширине образца, то можно получить следующее выражение:
![]() О» (ЫЬа) U £ (1/п ) (6/ба) Г,„ „.
О» (ЫЬа) U £ (1/п ) (6/ба) Г,„ „.
Обозначим параметр материала’б как минимальное изменение плотности энергии деформации при длине трещины, необходимой для распространения этой трещины. Условие расп|юстранения трещины может быть представлено следующим выражением:
Это выражение показывает, что для тела шириной и. изменение энергии при изменении длины трещины должно быть больше или равно величине ‘б. называемой критической ско|Юстью освобождения энергии деформации. І Іеобхолимо ОТМСІ ить, что критическая скорость освобождениям энергии деформации имеет размерность величины энергии на единицу площади и представляет собой степень освобождения энергии деформации на единицу площади роста трещины. Данное уравнение является основным для описания механики разрушения линейно-упругого мате
риала и используется для интерпретации результатов испытаний образцов, форма которых представлена на рис. 2.3. Очень важно оценить тонкий смысл этого анализа. Используя параметры, основанные на энергетических особенностях поведения материала, а не на напряжениях и деформациях, можно описать распространение трещины в материале, имеющем неопределенные форму и состав. Методы оценки критической скорости освобождения энергии деформации материала клеев рассматриваются и следующей главе.
Модуль продольной упругости и модуль упругости при сдвиге используют при проектировании конструкций, которые предназначены для эксплуатации при нагрузках ниже предела текучести. Значение величины скорости освобождения энергии деформации позволяет принять решение о том. какой материал должен быть использован для создания устойчивой к растрескиванию конструкции. Все существующие в настоящее время материалы нс лишены дефектов. Если какой-либо материал не обладает стойкостью к распространению дефекта, конструкция элемента изделия разрушается при более низких нагрузках, чем конструкция, не имеющая дефектов. В табл. 2.2 представлены значения скорости освобождения энергии деформации для некоторых известных материалов. Эти данные позволяют реально представить, почему сталь находит применение при строительстве зданий, а кремний не может быть использован в данном случае. І Іесмотря на то что его модуль Юнга не намного меньше модуля Юнга стали, распространение трещины в кремнии происходит, когда скорость освобождения энергии деформации превышает значение 3 Дж/м?. В случае стали для распространения трещины необходимо почти в 1000 раз больше энергии, чем для кремния.
|
Таблиц/! 2.2. Критическая скорость освобождения энергии деформации для некоторых известных материалов
|
 31 августа, 2015
31 августа, 2015  admin
admin 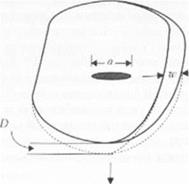
 Опубликовано в рубрике
Опубликовано в рубрике 