І Іскоторьіе основные положения теории балок приведены в разделе 2.7. В настоящем разделе целесообразно рассмотреть как эти положения реализуются в случае анализа изгиба субстратов в нахлестом ном образце |.5|. Значение такого анализа заключается в определении напряженного состояния клееного слоя. Данный аналитический метод начинается с рассмотрения уравнений (2.48). (2.50) и (2.60) и заканчивается уравнением (2.68). І Ізученис образца с нахлесткой, используемого при испытании на сдвиг, несколько отличается от анализа изгиба балки. Фактически данный метод представляет собой анализ состояния изгиба тонких, изогнутых по форме цилиндрических поверхностей. Однако в данном случае основные уравнения и их вывод аналогичны рассмотренным в п|н*дыдущей главе.
І Іа рис. 3.11 п|тедставлеио клеевое соединение, исследованное Голандом и Рейсис|х>м. Поставленная задача разделена на две части. Сначала исследуется изгиб субстрата, удаленного от области нахлестки. Эта область имеет длину / от торца « обрата. Затем рассматривается область нахлестки, которая имеет длину 2с. Естественно, что ІКЧНСНИЯ для каждого участка образца должны соответствовать такому положению, при котором эти участки находятся в непосредственном соединении. Эта задача аналогична прогибу батек и поэтому при анализе необходимо рассматривать моменты и силы сдвига. I (а рис. 3.12 схематически представлена система координат и направление, в котором действуют моменты и силы сдвига.
 ЗА
ЗА
![]()
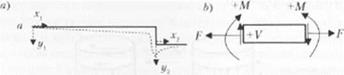 |
Схематическое изображение образца, рассмотренного Голандом и Рейснером. Длина субстратов составляет (/’ 2с). Линия нагружения находится между точками а н b и проходит через області» О. Субстраты имеют толщину г
![]() Схематическое изображение, представая книге основу. їли анализа нахлестом ноги образка за пределами клеевого шва. На схеме (а) показана нейтральная ось субстрата и центр клеевого шва до прогиба (сплошная линия) и после прогиба (пун м ирная линия) балки. Кроме того, показаны оси, рассматриваемые в данном исследовании: .г, и относятся к торцам субстрата, в то в|к’мн как з и у, относятся к краям нахлестки. 11а схеме (/>) показаны изгибающие моменты Af для меболыпо — го участка субстрата, силы сдвига V’и приложенная нагрузка F. Схема приведена в соответствии с правилом знаков, что должно учитываться при проведении полного анализа. (Схема взята из работы Іоланда и Рейтера.)
Схематическое изображение, представая книге основу. їли анализа нахлестом ноги образка за пределами клеевого шва. На схеме (а) показана нейтральная ось субстрата и центр клеевого шва до прогиба (сплошная линия) и после прогиба (пун м ирная линия) балки. Кроме того, показаны оси, рассматриваемые в данном исследовании: .г, и относятся к торцам субстрата, в то в|к’мн как з и у, относятся к краям нахлестки. 11а схеме (/>) показаны изгибающие моменты Af для меболыпо — го участка субстрата, силы сдвига V’и приложенная нагрузка F. Схема приведена в соответствии с правилом знаков, что должно учитываться при проведении полного анализа. (Схема взята из работы Іоланда и Рейтера.)
Анализ начинается с формулировки уравнений изгибающих моментов для положений I и 2. Согласно Роланду и Рейтеру выражения для изгибающих моментов имеют следующий вид:
Л/,-Flour,-у,) (3.1)
(32)
Эти уравнения получены исходя из геометрического рассмотрения моментов, возникающих в результате приложения нагрузки F. и нейтральной оси пластины. Необходимо заметить, что F. строго говоря, не является усилием, так как Ft представляет собой приложенное растягивающее напряжение. Угол а образован направлением приложения усилия и координатами т, иди. т, (рис. 3.11 и 3.12). Уравнение (2.(>(>) справедливо для каждого и» этих условий и в данном случае могут быть предложены следующие уравнения:
(33) (3.4)
В указанных уравнениях R называют жесткостью при изгибе пластин (субстратов), которая описывайся уравнением
• <35>
где F. — модуль Юнга; t — толщина: v коэффициент Пуассона материала пластины.
Приведенные выше четыре уравнения могут быть объединены в целях получения двух спаренных дік|к})ереїщиальных уравнений второго порядка, для которых может быть найдено тригонометрическое решение. Необходимо отметить, что в данном случае точно оп|>сделены два момента, связанные е величиной R, один момент для конца субстрата в точке а (с координатами г, и у,); вто|м»й. для точки вблизи клеевого слоя (с координатами, гг и у2).
В данном случае используются граничные условия н некоторые упрощающие допущения. Одним из таких допущений является то, что /?, точно соответствует fty’8, так как область нахлестки имеет толщину, приблизительно вдвое превышающую толщину субстрата. Для момента силы сдвига в облает и перехода от субстрата к нахлестке может быть предложен следующий вид уравнений:
![]() А/
А/
(3.7)
где k — описывается выражением
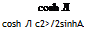
![]()
![]() (3.9)
(3.9)
Данные уравнения используются при анализе сил. действующих в области клеевою соединения.
ІГелесообразно теперь рассмотреть область нахлестки или, другими словами, область. обозначенную длиной 2с (рис. 3.11). Область нахлестки делится на два участка: на верхний участок, обозначенный символом и, и нижний имеющий символ /. 11а рис. 3.13 схематично показано такое состояние образца. И данном случае принято допущение, что деформация субстратов іі|юисходиі исключительно в результате воздействия продольного напряжения в направлении оси т субстрата. Учитывая это допущение, клееной слой в основном ведет себя как подчиняющееся закону Гука твердое тело, находящееся между двумя субсчетами. Как показано на рис. 3.13, клеевой слой разделен вдоль посередине. Применительно к нему определяют касательное (т) и нормальное (а) напряжения. На рисунке показаны также силы сдвига для каждого элемента (tlx) клеевого шва. Напряжения сдвига обозначены символами Г и Г. где подстрочные индексы относятся соответственно к верхнему и нижнему участкам образца. Аналогичным образом определяются и моменты (М). Используя в некоторой степени абсолютно аналогичный подход, который был применен Тимошенко (см. литературу к гл. 2) при решении описанных в предыдущей главе задач, связанных с поведением балки, можно записать следующие условия равновесия для верхнего и нижнего участков клеевого соединения.
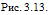 ( хематичсское представление об акали гическом анализе — облає ги нахлестки в соединении, подвергающемся воздействию сил сдвига. Обозначения с и t аналогичны показанным на рис. 3.11. Т толщина клеевого слоя На приведенных в нижней части рисунка схемах показана часть нахлестки длиной dx, которая делится соответственно на верхний (и) и нижний (/) участки, при «том о и т представляют соответственно растягивающие и сдвигающие напряжения. Па данном рисунке Г — нагрузка, приложенная к отрезку образца: V сдвигающая сила, приложенная к атому отрезку образца; М момент, приложенный к отрезку образца (схема взята из работы Голанда и Ренснсра)
( хематичсское представление об акали гическом анализе — облає ги нахлестки в соединении, подвергающемся воздействию сил сдвига. Обозначения с и t аналогичны показанным на рис. 3.11. Т толщина клеевого слоя На приведенных в нижней части рисунка схемах показана часть нахлестки длиной dx, которая делится соответственно на верхний (и) и нижний (/) участки, при «том о и т представляют соответственно растягивающие и сдвигающие напряжения. Па данном рисунке Г — нагрузка, приложенная к отрезку образца: V сдвигающая сила, приложенная к атому отрезку образца; М момент, приложенный к отрезку образца (схема взята из работы Голанда и Ренснсра)
![]()
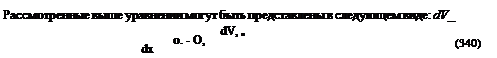 |
![]()
в том числе дли условии вертикальной равновесной составляющей:
![]()
![]() dF,
dF,
dx T — ” dx
її для условий равновесия сил. приложенных в направлении растяжения субстратов. Приведенные ниже уравнения
|
|
![]()
описывают равновесное состояние моментов в субстратах. Но аналогии с состоянием, расе мот репным в гл 2. и используя уравнение (2.66). можно записать следующее выражение для оценки вертикального перемещения верхнего и нижнего участков субстрата:
d‘i А/. d}v, .U,
R’ lx* ~~R’ (313>
где R жесткость субстрата при изгибе, определяемая но уравнению (3.5).
Далее приведены уравнения для оценки продольных перемещений субстратов вблизи клеевого слоя:
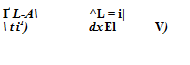
![]() (344)
(344)
І Іолнмй ряд уравнений, который был использован Голандом и Рейс пером. тля завершения анализа образцов, нртдетакляют собой соотношение между напряжением п де<|и)рмациеіі для материала клеевого слоя, соответствующее закону Гука, определяемое выражениями:
4, — Ц. О.
Ga т ’ Ея Т ‘ (345)
где Сл п Ек — модуль упругости при сдвиге п |>астяжении.
Обработка всех приведенных выражений начинается с подстановки уравнения (3.11) в первое нз уравнении (3.15), двойного дифференцирования относительно х с учетом уравнений (3.11) и (3.12). В данном случае можно записать следующее выражение:
d т 8СЛ dx п
dxг’ HtT dx (346)
Уравнение для а„ может быть получено аналогичным способом при использовании второй части уравнения (3.15). применяя двойное дн<|)фсрснци|нтание п подстановку уравнения (3.13). что приводит к получению следующего выражения:
1 d7a 1 А/,-А/.
Е. лdx’ ~Т К
І Іовторио дифференцируя это выражение и используя уравнения для равновесия моментов (3.12) и условия равновесия сдвигающих сил, описываемое уравнением (3.10), получаем выражение
1 ЛЧ 2
Ел dx’ " TDa(318)
Для решения любого ряда дифференциальных уравнений должны быть введены граничные условия, и такие решения должны находиться в соответствии с физической сущностью рассматриваемой задачи. При решении уравнений (3.16) и (3.18) граничными условиями являются:
при г — с, М — Тл — V — 0 и М. = Л/0 и V, = Vn и F — F
при х — — с. М, ‘Гг V’ — 0 и М" — — А/0 н У — и Fa — F.
Необходимо отметить, что граничные условия включают силу сдвига Vj, и момент Л/м, которые были определены для субстрата в области края нахлестки. Приведенные граничные условия объединены с выполненным выше анализом и представ ляют следующие граничные условия для оценки растягивающей силы к клеевом слое:
и
![]() J xndx + F = 0,
J xndx + F = 0,
которое является условием равновесного состояния.
И наконец, іраничіше условия для растягивающих сил могут быть представлены в следующем виде:
Ел w
Iipii. v-±c, fai ~yr • (3.21)
и
![]()
![]() (3.22)
(3.22)
|
^(1 + 3*) t |
После применения граничных условий к приведенным выше Д11(|к[)ерепциальньім уравнениям напряжение сдвига в клеевом слое описывается следующим уравнением:
Выше было показано, что член Сланного уравнения прслставляет собой напряжения в субстрате вдали от области клеевого соединения. Уравнение для растягивающих напряжений в клеевом сдое имеет значительно более сложный вид. чем уравнение для напряжения сдвига, и может быть записано в форме:
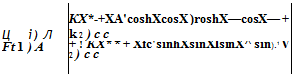 (3.25)
(3.25)
 |
|
Эго чрезвычайно сложное выражение оказывается еще более сложным, когда рассматриваются включенные в него члены, а именно:
![]() К,= sinhXcosX + cosh X sin X;
К,= sinhXcosX + cosh X sin X;
Д — (sinh2X * sin2X)/2 (3.29)
и
Рассмот|>снные выше математические выражения являются очень сложными и приводят к появлению трудно воспринимаемых уравнений. Однако необходимо отметить, что большинство членов приведенных выше уравнений относятся к рассмотренным в П|)сдыду1цей главе понятиям, например, модулю упругости, кож|)фициен гу І Іуассоиа, моментам, силам сдвига и изгибу балок Довольно правильным подходом к восприятию этих уравнений является рассмотрение графика зависимости напряжений при сдвиге и растяжении в клееном слое от расстояния от центра клеевого соединения. Эти графики представлены схематично на рис. 3.14 и 3.15.
На рис. 3.14 показано, чю напряжения сдвига п соединении не являются абсолютно однородными. Кроме і ого, в центре клеевого соединения величина напряжения сдвига меньше, чем среднее значение напряжения сдвига в клеевом соединении, тогда как у края соединения напряжение сдвига имеет значительно большую величину, чем среднее значение напряжения сдвига в клеевом соединении.
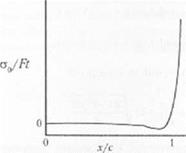
Аналогичная ситуация имеет место при расчете и графическом изображении кривой растягивающих напряжений (рис. 3.15). Необходимо отметить, что когда говорят о растягивающих напряжениях в клеевом слое, имеют в виду напряжения, которые являются перпендикулярными (или «нормальными») по отношению к исходному растягивающему напряжению, приложенному к субстрату. Другими словами. направление приложения этих напряжений перпендикулярно клеевому шву. Из данного рисунка видно, что в цснт[>с соединения [«стягивающее напряжение равно нулю. Это объясняет некоторые из наблюдаемых эффектов при испытали-
|
Рис. 3.14. Схематическое представление результатов анализа Голанда-Рейснера для напряжения сдвига в соединении внахлестку (деленное на растягивающее напряжение, приложенное к субстрату) в зависимости от расстояния от центра клеевою сосди нения |
|
Рис. 3- іх Схематическое изображение графика зависимости растягивающих напряжений в клее (отнесенных к растягивающему напряжению, приложенному к субстрату) от расстояния от центра клеевого соединения |
ях конструкционных клеев на сдвиг на образцах с нахлесткой. В центре соединения часто наблюдается когезионное разрушение по клеевому слою, несмотря на то что визуально определяется адгезионное разрушение на некотором расстоянии от центра образца. Нормальные напряжения п клеевом шве являются максимальными у краев нахлестки. Это явление можно мысленно представить, оценивая, какая часть клеевого соединения должна иметь максимальный изгиб, чтобы сделать линейным приложенное усилие. Одним из вопросов, который не всегда очевиден при математическом анализе, является образование области сжатия непосредственно перед резким увеличением растягивающего напряжения. В том случае, когда прикладывается рычаг, должна существовать точка опоры. Область сжатия, рассматриваемая в данном анализе, показывает, что точка опоры для рычага, образованного субстратом, находится непосредственно за областью максимального изгиба но направлению к центру клеевого соединения. Далее в настоящей главе будет рассмотрено подобное состояние образца. Наличие нормальных напряжений в таком соединении имеет важные последствия, которые будут рассмотрены в гл. 8.
 10 сентября, 2015
10 сентября, 2015  admin
admin 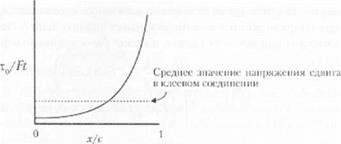
 Опубликовано в рубрике
Опубликовано в рубрике 