Иногда высказываются предположения, что для описания связи между силами адгезии и реальной прочностью клеевого соединения математической модели не существует. В данном разделе приведены результаты некоторых экспериментов, которые представляют собой основу для определения связи между свойствами границы раздела и механической прочностью клеевого соединения. Эти эксперименты, свя-
занныес исследованием эластомерных материалов. позволили получить математическое выражение, описывающее физическую основу процесса.
При рассмотрении силановых соединяющих агентов эффективность химического взаимодействия проявляется в повышении долговечности композиционного материала. Модуль упругости композиционного материала практически одинаков как при использовании, так и в отсутствии силана, однако модуль упругости материала при воздействии жестких условий окружающей среды сохраняется на более высоком уровне в случае присутствия силана на границе раздела.
Существуют также примеры увеличения прочности клеевого соединения в исходном состоянии в результате использования соединяющего агента. Эти экспериментальные исследования были описаны Эйхагоном и Гентом [30]. На стеклянный образец была нанесена смесь винилсилаиа и этилсилана. представляющая собой практически монослой. Винилснлан может реагировать с верхним слоем, отверждающимся по свободнорадикальному механизму, но этилсилан не вступает с ним в реакцию. Автор считает, что увеличение процентного отношения винилсилаиа по сравнению с этилсиланом должно приводить к увеличению значения сил адгезии. Эйхагон и Гент наносили слой иолнбутадиена на обработанный силаном образец поверхности и создавали в нем поперечные связи но свободнорадикальному механизму. Прочность клеевого соединения определяли при испытании на отслаивание под углом 180“, при этом полибутадиен отслаивали от образца при различных температурах и скоростях приложения нагрузки. Результаты эксперимента были совмещены путем использования коэффициентов сдвига для получения обобщенной кривой для испытаний на отслаивание по каждому варианту обработанной поверхности. Обратите внимание на рассмотриные в предыдущей главе обобщенные кривые и принцип температурно-временной суперпозиции для полимеров.
Схематическое изображение полученных Эйхагоном и Гентом результатов показано на рис. б. 16. Кривая, обозначенная символом VI’,. относится к образцу, на поверхности которого находится исключительно этилсилан, в то время как символ W относится к кривой для образца, на поверхности кото|к>го присутствует исключительно винилснлан. Символы IV. и IV, показывают промежуточные содержания винклси лана в смеси с этилсиланом. Символ IVбыл выбран не только для оценки этих кривых, но также для асимптотического обозначения работы, приводящей к разрушению клеевого соединения. Обратите внимание, что IV, > W, > IV, > IV. Данные результаты удовлетворительно согласуются с содержанием винилсилаиа в покрытии образца.
Этот график может быть использован для получения представления о некоторых вопросах, связанных с адгезией. Во-первых, на графике зависимости прочности при отслаивании (работа до достижения разрушения) от скорости отслаивания может появиться асимптотическое значение, которое можно описать как работу адгезии. Во-вторых, кривые зависимости работы при разрушении от уменьшения скорости отслаивания имеют обычно одинаковый характер, но эти кривые сдвинуты в вер — тнкалыюм направлении относительно друг друга. Обратите внимание, что график выполнен в логарифмических координатах. Для такого состояния можно записать следующее выражение:
|
или, записывая это выражение н виде антилогарифма, получаем:
У.-ИХ. (6.17)
Это уравнение показывает важную связь между прочностью клеевого соединения и произведением некоторого коэффициента, описывающего силу адгезии, и другого коэффициента ц. Этот коэффициент £ должен относиться к реологическим свойствам клея (верхнего слоя), гак как по оси абсцисс на рис. С». 1G откладывается значение скорости отслаивания, умноженное на коэффициент смешения. Это свя — занос вопросами, рассмотренными в гл. 5. и особенное данными, приведенными на рис. 5.11. на котором представлен ірафнк зависимости логарифма модуля от частоты. умноженной на коэффициент смещения. Вполне допустимо рассматривать коэффициент £ как параметр, описывающий свойства материала, входящего в структуру клеевого соединения, влияющие на способность рассеивать энергию (например, вязкоупругость). Последней особенностью, отмеченной в данном разделе, является наличие асимптотических значений работы, затрачиваемой на разрушение клееного соединения. Установлено, что эта величина составляет порядка от 200 мДж/м1 до примерно 2 мДж/мг. что находится в пределах одного или двух значений величины работы сил адгезии, которая получена из вычислений в соответствии с уравнением Нмга-Дюпрэ. Приведенное выше уравнение и экспериментальные данные показывают взаимозависимость между связью на границе раздела, способностью клеевого слоя рассеивать энергию и механической прочностью клеевого соединения.
Важным моментом, рассматриваемым в данной книге, является вопрос о существовании каких-либо других экспериментальных данных, подтверждающих справедливость этого уравнения. В одной и t серий исспсрпмснтальных исследований, выпал-
нснных Гентом п Шульцем [31), прочность при расслаивании соединения клеевой слой-субстрат определялась после воздействия различных жидкостей. В отличие от образования поверхносги с определенной меж()шной энергией на границе раздела с воздухом в данном исследовании межфазная энергия зависела от жидкости, в среде которой проводились эксперименты но оценке устойчивости к отслаиванию. Работу, необходимую для разрушения соединения, определяли в зависимости от скорости отслаивания, при этом скорости смешались практически так. как описано Эйхагоном и Гентом. В данном случае было получено семейство кривых, имеющих приблизительно одинаковую форму. Однако эти кривые смешены относительно друг друга. Это смещение определяется межфазным поверхностным натяжением, существующим между поверхностями и жидкостью, используемыми в данном эксперименте.
В другой работе Эндрюс и Кинлох 132) использовали простые образцы для испытаний на разрушение, в которых моделировалось клеевое соединение. Они определяли скорость распространения трещины в специально введенном в клеевое соединение дефекте в зависимости от работы сил адгезии между субстратом и клеевым слоем. Скорость распространения трещины уменьшали и в соответствии с коэффициентом смещения был построен график зависимое ї й логарифма усилия, необходимого для распространения трещины, от логарифма уменьшении скорости раскроет ранения трещины. В данном эксперименте было получено практически параллельное семейство кривых. Кривые оказались смещенными относительно друг друга на величину, приблизительно соответствующую работе сил адгезии. Обе работы Гента и Шульца и работа Эндрюса и Кинлоха подтверждают справедливость уравнения (6.19).
Могис (33) исследовал скоростную зависимость распространения межфазной трещины между полиуретановой с<|>срой и поверхностью стекла, используя метод JKR (см. раздел 4.5.2 2). В результате этих исследований он установил, что работа. необходимая для разрушения адгезионного соединения, образованного между этими двумя поверхностями, зависит от уменьшенной скорости распространения трещины примерно в степени 0.5. В серии других экспериментальных исследований. выполненных Шуллом с сотр. (34), были получены аналогичные результаты, в которых были использованы материалы, имитирующие чувствительные к давлению клеи.
Можно предложить ||и? номенологичсское описание этого явления с точки зрения молекулярною строения Молекулы полимера и клее могут быть представлены в виде большого количества спагетти, помешенных между двумя субстратами. Спагетти частично отварены, поэтому их частицы немного слипаются и переплетаются между собой Принимают, что спагетти имеют достаточно большую длину, чтобы ими і кровать полимерные молекулы, молекулярная масса которых превышает значение их молекулярной массы в этом сложном переплетенном состоянии. Аналогия со спагетти позволяет понять многие вопросы физики полимеров. Однако нельзя распространять эту аналогию слишком широко. Спагетти находятся в неподвижном состоянии, в то время как молекулы полимера находятся в постоянном движении.
Предположим сначала, что спагетти не соединяются с субстратом. Растягивание соединения удаляет часть спагетти с поверхности субстрата. Следовательно, если 1Г4 ■ 0. то и U; — 0. Предположим теперь, что спагетти прилипают к поверхности.
Если растягипать субстраты, спагетти не будет отделяться от субстрата. Отчасти механическая энергия расходуется на растягивание спагетти. Если спагетти в достаточной степени переплетены, механическая энергия продолжает расходоваться на растягивание и распутывание спагетти. Величина, на которую спагетти могут быть растянуты, зависит от того, насколько они прилипли к субстрату. Силу адгезии спагетти к субстрату нельзя определять до тех нор, пока хотя бы одна из них находится в натянутом состоянии. Однако в определенной точке клен уже адсорбировал большую часть механической энергии. Таким образом, адгезия, которую спагетти проявляют но отношению к субстрату, увеличивает способность клея поглощать механическую энергию. Величина механической энергии, которая может быть рассеяна в Blue энергии межмолекулярного взаимодействия, необходимой для растягивания молекул полимера, зависит от энергии взаимодействия «полимер-полимер» (иногда называемой молекулярным трением) и от того, насколько сильно полимер прилип к поверхности Чем выше сила адгезии, тем большая величина энергии может быть израсходована на растягивание полимера. Так как можно считать, что сила адгезии, демонстрируемая клеем, имеет промежуточную величину, которая увеличивает’ абсорбцию сил энергии клеем: нетрудно предположить, что увеличение адгезии должно приводить к повышению энергии, способной поглощаться клеевым слоем.
Далее рассмотрим более общее уравнение, описывающее связь между практической работой адгезии и теоретической адгезией. Из анализа критерия разрушения Гриффитса известно, что в случае абсолютно хрупкого материала энергия, необходимая для разрушения клеевого соединения, описывается выражением — WA, которое представляет собой параметр 2у или у, + у, — у|2, зависящий от того, имеет ли разрушение когезионный характер по клею или разрушение носит адгезионный характер. Можно считать, что эта энергия представляет собой минимальное значение практической адгезии, которую можно реализовать в клеевом соединении. Если имеется возможность рассеяния энергии, как. например, благодаря более высокой адгезии и молекулярного трения, это минимальное значение энергии возрастает. Работа Эхагона и Гента (и других авторов) показывает, что величина этого возрастания энергии пропорциональна параметру и имеет вид
WWWX. (6.18)
Это уравнение показывает, что неизвестная функция работы сил адгезии /(И’,) умножается на параметр £, что, в свою очередь, показывает, как механическая энергия рассеивается в клеевом слое н субстрате.
На основании уравнения (6.19) также можно показать, что если логарифм 1ГЛбыл определен при более низких или значительно уменьшенных значениях скоростей (например, при очень низких скоростях или высоких температурах или в случае совместного использования этих двух переменных), в конечном итоге приходят к точке, в которой определяют функцию/(U’). При нулевой скорости £ имеет малую величину. Чтобы уравнение (6.19) оказалось справедливым, значение этого параметра должно быть около 1. Приведенные в литературных источниках результаты измерений показывают, что экстраполированные значения логарифма U’s, полученные при очень низких скоростях, практически не соответствуют уравнению Дюпрэ.
Более того, асимптотическая величина работы, по-видимому, достигает опрелслсн — ного ряда значений, которые зависят от типа связей на границе раздела. Например, в работе Брауна с сотр. [8) было установлено, что асимптотическое значение WA для полистирола, контактирующего с полиизопреном, составляет около 120 мДж/м2, в то время как величина этого параметра (в соответствии с уравнением Дюпрэ) равна 65 мДж/м2. В случае блок-сополимера, присутствующего на границе раздела, асимптотический уровень увеличивается до 400 мДж/м2 в зависимости от поверхностной плотности полимерной цепи на поверхности и длины сегментов блок-сополимсрнон цепи. В процессе другого экспериментального исследования, описанного Чангом и Гентом, образцы полибутадисна были сначала частично вулканизованы, соединены друг с другом и затем окончательно вулканизованы. Эти соединения затем подвергали расслаиванию при различных скоростях нагружения и темпе|>атурах и строили график зависимости логарифма усилия отслаивания от логарифма скорости уменьшения усилия. Экстраполяция к низким коэффициентам уменьшения скорости нагружения приводит к величине собственной энергии адгезии около 1 Дж/м2. Эта величина практически соответствует значению, которое можно было бы предсказать для границы раздела, представляющей собой связи углерод углерод, которые описаны в разделе 6.8. Этот анализ показывает, что параметр, обозначенный как/( W2) в уравнении (6.19), должен быть заменен параметром *§0, который может быть назван пороговой (или собственной) работой сил адгезии в случае специфического соединения. Таким образом, величина параметра 9»с составляет около 60 мДж/м2, когда силы адгезии определяются исключительно наличием ван-лер-ваальсового взаимодействия, и около 400 мДж/м2, когда стабильность границы раздела обеспечивается стойкостью к выдергиванию полимерной цепи. Однако параметр^ ранен одному или нескольким Дж/м2, если при соединении двух поверхностей присутствует ковалентная связь.
В данной работе представлено уравнение, которое следующим образом связывает теорет ические значения сил адгезии с практической адгезией эластомеров:
Ия-^(1 + (гаТ), (6.19)
где г — какое-то число, которое лежит п пределах 0.3 0,6 в ограниченной серии экспериментов: г скорость, при которой происходит процесс расслаивания соединения: ат— кож|к|ишііепт смешения для температурно-временной суперпозиции: —
собственная энергия адгезии.
Это уравнение описывает современное понимание автором связи между адгезией на молекулярном уровне, механизмами рассеяния энергии в полимерах и работой разрушения простых клеевых соединений, полученных с применением эластомерных клеев.
 25 августа, 2015
25 августа, 2015  admin
admin 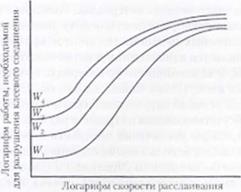
 Опубликовано в рубрике
Опубликовано в рубрике 