Поверхности и межфазные границы представляют собой границы раздела между различными состояниями вещества, между различными химическими веществами и между совокупностью таких химических веществ, как материалы или живые существа. В первую очередь, для таких материалов, как жидкости, характерно ясно выраженное проявление поверхностных сил. Если попытаться медленно нажать каким-то стержнем на поверхность чистой жидкости, например, воды, можно почувствовать сопротивление, которое оказывают поверхностные силы. В природе поверхностные силы позволяют, например, насекомым перемещаться по поверхности воды. Межфазные силы приводят к явлению капиллярного подъема, которое наряду с одновременным просачиванием позволяет жидкостям перемещаться от корней к кроне деревьев. Тот факт, что жидкости обладают поверхностной энергией, можно также подтвердить простым воображаемым экспериментом. Например, известно, что все природные вещества стремятся принять свойственное им наименьшее энергетическое состояние. Почему?
Жидкости обладают избыточной энергией, связанной с поверхностью. Сферы имеют наименее возможную площадь поверхности среди любых трехмерных объектов. Так как все вещества имеют тенденцию принимать наименьшее энергетическое состояние, капли жидкости принимают сферическую форму (при отсутствии гравитационного искажения формы), и поэтому энергия, связанная с существованием поверхности, оказывается минимальной. Грамотное представление о поверхностях и термодинамике поверхности имеет существенное значение дія понимания вопросов, связанных с явлением адгезии и клеящими материалами. Поверхность раздела играет решающую роль не только при формировании клеевого соединения, но также при передаче напряжений после образования этого соединения.
Адамсон [9] предюжил простое основанное на молекулярной теории объяснение тому факту, почему жидкости обладают избыточной энергией, связанной с их поверхностью. Давайте представим себе молекулы в жидкости в виде скопления шариков, взаимодействующих друг с другом в результате воздействия описанной выше системы сил. Молекула в объеме жидкости в одинаковой степени взаимодействует со всеми ближайшими соседями. Однако молекула, которая находится на поверхности, может взаимодействовать только с молекулами, расположенными ниже или сбоку от нее. Для такой молекулы характерна «некомпенсированная валентность». Для того чтобы нейтрализовать этот дисбаланс сил на поверхности, молекулы имеют склонность к дальнейшему разделению, таким образом увеличивая силу, действующую в плоскости поверхности. Этот момент приводит к ощущению, что жидкость имеет какую-то «оболочку». Действительно, экспериментально было показано, что жидкости (в тройной точке на диаграмме состояния) имеют более низкое значение плотности в поверхностной области [10]. Таким образом, можно объяснить наблюдаемое явление тем. что поверхностные силы являются результатом дисбаланса между межмолекулярными силами для молекул, которые присутству
ют на границе раздела между фазами и материалами. Это описание использовано в работе как метод оценки поверхностной энергии применительно к жидкостям, для которых характерно простое (ненаправленное) взаимодействие между атомами и молекулами.
Предположим, что энергия взаимодействия между двумя молекулами А задана величиной х• В упрощенной модели ближнего порядка молекула имеет ближайших соседей, где г обозначает координационное число и b — «объем» (внутри жидкости). Таким образом, общая энергия взаимодействия между рассматриваемой молекулой и ее ближайшими соседями описывается уравнением
![]()
![]()
![]() (4 19)
(4 19)
На поверхности координационное число будет иметь некоторую величину, меньшую, чем гу Обозначим координационное число на поверхности символом zt. Следовательно, энергия взаимодействия молекулы с ее соседями на поверхности может быть представлена уравнением
![]() (4.20)
(4.20)
В обоих выражениях значение энергии взаимодействия делится на два для того, чтобы преобразовать результат по отношению к двойному счету. Таким образом, разница энергии молекул на поверхности от энергии молекул в объеме может быть описана выражением
где а — площадь поверхности, занятая молекулой А; у — параметр, называемый поверхностной энергией.
Другие методы оценки эффекта молекулярных взаимодействий между двумя поверхностями описаны в работе Фаулера и Гуггенхайма (11]. Данный метод расчета аналогичен другим методам, описанным в литературе, и его основной принцип показан на рис. 4.2. 13 этом методе предусмотрены два важных допущения. Первое допущение заключается в том. что плотность молекулы является постоянной на каждой стороне взаимодействующих поверхностей. Это неправильно с точки зрения молекулярной теории. Однако качественный анализ показывает, что это вполне приемлемо для данного рассмотрения. Второе допущение связано с тем, что каждая точка на любой стороне взаимодействующих поверхностей находится под воздействием описанных выше сил Леннарда-Джонса.
Полный интеграл, используемый в данном расчете, может быть представлен в виде
![]()
![]() (4.22)
(4.22)
В данном выражении п — плотность молекул на любой стороне двух поверхностей; а — расстояние, разделяющее две поверхности; А и В — постоянные притяжения и отталкивания Леннарда-Джонса. соответственно. Расчет начинают с определения количества молекул в кольцеобразном слое на расстоянии г при варьировании угла (Ю и взаимодействия всех возможных колен на крайней левой поверх-
|
Рис. 1.2. Схема метода расчета, щк-.іложеиного Фаулером и Гуггенхаймом. 11а схеме пред ставлены показатели, но которым проводится интегрирование. Основная идея расчеіа заключается в суммировании всех взаимодействий между всеми элементами на одной стороне поверхности раздела со всеми элементами на другой стороне (рисунок из работы Фаулера и Гуггенхайма) |
ности в точке на крайней правой поверхности. После этого уравнение интегрируют относительно всех возможных точек на крайней нравом поверхности.
Далее обратим внимание на общую энергию £г необходимую для разделения этих двух поверхностей на бесконечное расстояние. Интегрируя общую силу по всем расстояниям от равновесною расстояния до бесконечности, получаем
= Г*"/? ‘tin — (4.23)
В данном выражении сила, умноженная на расстояние, представляет собой энергию. Подставив уравнение (4.22) в уравнение (4.23). получаем следующее выражение. описывающее общую энергию взаимодействия между двумя рассматриваемыми поверхностями:
|
|
При условии, что при гД равновесное расстояние) общая сила равна нулю, можно записать
А Н
12 УОг* <12Г>)
Полодии в это уравнение в выражение для общей энергии (4.24). подучаем
, кп’Л .. юс’Л
Я26)
Это уравнение имеет решающее значение для данного раздела книги. Используя метод Фаулера и Гуггенхайма, вычислена полная энергия взаимодействия, характерная для двух поверхностей, чьи молекулы взаимодействуют при помощи силы Леппарда-Джонса. Установлено, что взаимодействие зависит от плотности молекул на поверхности, равновесного расстояния между двумя поверхностями (которое
можно также рассматривать как мсжмолскулярнос расстояние, приняв допущение, что обе поверхности действительно находятся в контакте в равновесном состоянии) и постоянной притяжения Л. Благодаря присутствию двух контактирующих поверхностей общая анергия зависит от межмолскулярных сил. существующих в материале. и от межмолекулярного расстояния. Уравнение (4.26) позволяет определить величину у, которая представляет собой половину общей энергии взаимодействия. Как показано выше, параметр у является поверхностной энергией материала. Необходимо отметить, что значение параметра у зависит от величины межмолекулярных сил. что определяется ее зависимостью от постоянной А. Обратите внимание, что математическая <(юрма выражения, выведенного с использованием коорлинацион — ного числа (уравнение (4.21)). аналогична уравнению (4.26).
Поверхностная энергия у играет определяющую ]я>ль для понимания явления адгезии. В данном случае необходимо отчетливо представлять, что данная величина представляет собой точно такой же параметр материалов, как прочность при растяжении или другие характеристики материалов. В табл. 4.1 приведен перечень экспериментально полученных значений поверхностной энергии дня некоторых известных жидкостей.
|
Таблица 4 1 Значения поверхностной энергии известных жидкостей
|
Рассмотрим теперь взаимосвязь между поверхностном энергией и жесткостью материала. Изотермический модуль Юнга материала может быть представлен в виде[12|
![]()
![]() (4.27).
(4.27).
Подстрочные индексы показывают, чтолиі|и|н-рсчшнал вычислен при постоянной температуре и при г — г„. В данное выражение может бы ть подставлен потенциал Леппарда-Джонса. Используя алгебраические вычисления и аргумент равновесного расстояния. находим
С = (4 28)
*11
Используя уравнение (4.26), можно записать
Этот чрезвычайно интересный |>езультат показывает, что изотермический модуль Юнга напрямую связан с поверхностной анергией материала. В данном случае очевидно, что материалы, дли которых характерна наибольшая жесткость, также обладают и наибольшей поверхностной энергией. Аналогичная связь может быть продемонстрирована относительно других параметров, связанных с когезионными свойствами материалов.
 19 августа, 2015
19 августа, 2015  admin
admin 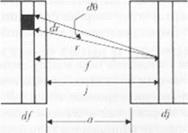
 Опубликовано в рубрике
Опубликовано в рубрике 