В рамках данной книги для понимания адгезии и принципов создания клеев важным является установление связи результатов измерения краевого угла смачивания с основными силами, действующими между атомами и молекулами. Плодотворные работы в данной области были опубликованы в 1950-х гг. Гудом и Джирифалко (31 ]. Для того чтобы получить правильное представление об этой работе, необходимо, в первую очередь, понять еще один важный аспект поверхностной энергии, который рассматривают как термодинамический параметр. С помощью рис. 4.10. можно представить себе воображаемую ситуацию с частью поверхности, показанной на рисунке в виде свободного тела.
Предположим, что есть линия (показана пунктиром), которая проведена где-то в рассматриваемом теле. Предположим также, что существует сила, действующая поперек этой линии (рис. 4.10). Рассмотренные выше воп|юсм показывают, что для поверхности характерно сопротивление ее деформированию. Если поверхность является жидкостью, то величина такого сопротивления представляет собой «поверхностное натяжение». Если поверхность деформируется, например, с увеличением площади, то над этой системой производится работа. Согласно Черри (32]. можно описать внутреннюю энергию системы следующим уравнением
d$=dq-dw+’£ii, dN„ (4.50)
I
где q — внутренняя энергия системы; ц — теплота; w — работа; ц, — химический потенциал /-го компонента системы; Nt — число молей i-ro компонента в системе.
|
Рис. 4.10. Часть поверхности, через которую проведена пунктиром воображаемая линия Действие поверхностного натяжения распрос траняется в двух направлениях относительно этой линии Применительно к жидкости поверхностное натяжение и поверхностная энергия имеют как одну и ту же величину, так и одинаковый смысл |
Для ситуации, имеющей важное значение при анализе данного вопроса, работа в системе включает не только обычно рассматриваемую составляющую, связанную со взаимоотношением давление (Я)-объем (V), но так как система находится на поверхности. она также может выполнять работу, связанную с увеличением площади поверхности. Таким образом
thv — PdV — -/dii. (4-51)
где LI — площадь поверхности.
Изменение теплоты в системе определяют, применяя термин энтропия (5):
dq = 7US. (4.52)
Используя приведенные выше уравнения и принимая, что система находится при постоянных температуре, давлении и значении числа молей материала, можно доволі, по просто показать, что
d = TdS PdV+fdLl+^V’dN’. <453)
І
Свободная анергия системы но Гельмгольцу описывается уравнениями
Л = $-Г5 (4.54)
и
dA = ydCl-PdV — SdT ♦ ХМ//ЛГ,. (4 55)
I
которые, если рассматривать систему, находящуюся в условиях постоянного объема. температуры п при постоянном числе молей материала, приводят к получению выражения
f-1 •
UU™ (4 56)
Важное значение этого уравнения заключается в том. что поверхностная энергия может быть описана как изменение свободной энергии термодинамической системы в зависимости от изменения ее площади. Аналогичное преобразование может быть сделано для свободной энергии Гиббса (7. и в данном случае уравнение принимает вид
«да
Свободная энергия Гиббса и свободная энергия Гсльмшльца связаны следующим соотношением:
(J=A + PV (4.58)
Следовательно, описанная выше работа сил когезии и работа сил адгезии также представляют собой термодинамические переменные. Это заключение и определение поверхностной энергии как переменной свободной энергии являются основой для вывода уравнений Гуда-Джирифалко.
 20 августа, 2015
20 августа, 2015  admin
admin 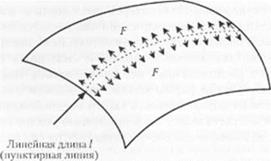
 Опубликовано в рубрике
Опубликовано в рубрике 