В настоящем разделе не делается различия между модулем Юнга и модулем упругости при сдвиге, а описываются параметры, определяемые как модуль накопления, модуль потерь и tg 6. Типичный динамический механический спектр для модуля накопления аморфного полимера представлен на рис. 5.7. Па оси температуры не показаны ее абсолютные значения, так как это типичная кривая. Необходимо отметить. что кривую аналогичной формы получают для любых аморфных полимерных материалов независимо от их типа. Смещения кривых происходят вдоль температурной оси или в вертикальном направлении вдоль оси модуля, однако общие особенности этих кривых в значительной степени аналогичны характеру кривой, приведенной на рис. 5.7.
Диаірамма модуля потерь этого типового аморфного полимера имеет (|юрму, аналогичную показанной на рис. 5.7, за исключением того, что кривая имеет перевернутый вид, т. с. материал обладает более высокой величиной модуля потерь при таких температурах и частотах, при которых его модуль накопления оказывается низким.
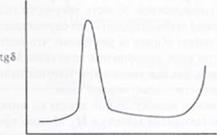
Диаграмма для tg6 того же самого типового аморфного полимера выглядит аналогично кривой, представленной на рис. 5.8. Обратите внимание, что для кривой tg б характерен максимум приблизительно в той же точке, в которой кривая модуля накопления имеет максимальный угол наклона. Специалисты часто определяют по максимуму кривой tg5 температуру стеклования. Однако важно отметить, что положение максимума угла наклона кривой или положение максимума на кривой
|
Модуль упругости П СТ1КЛ(х/>|ЬЧ1|К>и СОСТОЯНИИ
|
Hue. 5.7. Обобщенный динамический механический спектр для аморфного термопласта Обратите пннманнс. что модуль упругости полимера резко уменьшается при достижении температуры стеклования и. что на оси абсцисс может быть отложена или температура, или частота. Аналогичные кривые получают для любых перс менных значений параметров, за исключением тех случаев, когда направления их воздействия взаимно противоположны
|
Температура — » Частота ■*— |
Hue 5.8 График. сипн имогти логарифма модуля потерь от частоты или температуры Об ратите внимание на обратную зависимость от частоты и температуры. Пик на кри вой точно соответствует положению температуры стеклования при частоте измерения
модуля потерь зависит не только от температуры, но и от частоты. Таким образом, если определяют механический динамический спектр какого-либо полимера при определенной температуре, но при различных частотах, получают кривую, анало — I ичную приведенной выше, за исключением того, что на оси абсцисс представлено изменение частоты вместо температуры. В данном случае важно не только оценить температуру стеклования, но также частоту, при которой проводились измерения, позволившие получить указанные данные, .’ho свойство вязкоупругих материалов известно как температурю-временная суперпозиция.
На рис. 5.9 представлена температурно-частотная зависимость динамического механического спектра термореактивного полимера как функции от густоты сетки. Параметр А/ представляет собой размер блока между поперечными связями. Как
|
Температура—- ». Частота •*— |
tbii 5.9 Динамический механический спектр для термореактивного полимера, показывающий влияние изменений плотности полимерной сетки или Л/
можно видеть, величина и протяженность модуля накопления на участке кривой, параллельном оси абсцисс, зависят от параметра Л/ . Обратите внимание, что когда значение параметра Л/ уменьшается, область текучести полимера начинает исчезать. Такое поведение можно п|К>пюзирокать для случая какого-либо термореактивного полимера. Также следует обратить внимание, что величина уменьшения модуля накопления падает по ме|>е уменьшения величины А/. Такое поведение также можно было предположить, так как увеличение илотност и полимерной сетки означает уменьшение подвижности молекулярной цени.
В книге показано влияние молекулярной массы на вязкость расплава и молекулярную массу переплетающихся молекул Л/,. Можно предположить, чго динамический механический спектр также в некоторой степени зависит от увеличения молекулярной массы. Па рис. 5.10 показано, что увеличение молекулярной массы полимера приводит к повышению температуры, при котором проявляется текучесть полимера. Этот :м|>фект заметен по увеличению протяженности плато эластичности. Характер поведения полиме|юв, который отражен на рисунках, приведенных в данной главе, играет определенную роль при анализе свойств конструкционных клеев, клеев-расплавов и, главным образом, чувствительных к давлению липкий клеев.
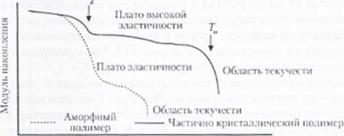
Па рис. 5.11 представлен динамический механический спектр частично кристаллического полимера. Кристаллиты создают э<|к}>ект «физических поперечных связен*. Другими словами, подвижности полимера п[>еііятствует наличие в его цепи кристаллитов. Это приводит к возрастанию как значения модуля на участке кривой, параллельной оси абсцисс, так и протяженности этого участка кривой.
И наконец, па рис. 5.12 представлен динамический механический спектр для сплава полимеров, который разделяется на две фазы. Такая зависимое! ь может быть характерна для блок-сополимеров. Другими словами, вместо образования одной непрерывной гомогенной фазы в материале образуются две одновременно сушест вую — щие фазы, каждая из которых облатает собственными свойствами. В данном случае можно предположить о наличии двух значений температуры стеклования.
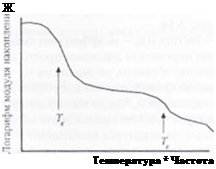 |
Рис 5 11. Динамический механический спектр, показывающий различие межлу повелением
аморфного и частично кристаллического термопластичных полимеров
!*ис. 5 12 Динамический механический спектр для аморфного блок-сополимера, который иокллынаег. что отдельные части блок-сополимера представляют собой самостоятельные фазы, характеризующиеся своими значениями температуры стеклования

/’иг. 5.10. Динамический механический спектр аморфного термопластичного полимера, показывающий влияние увеличения молекулярной массы
|
 22 августа, 2015
22 августа, 2015  admin
admin 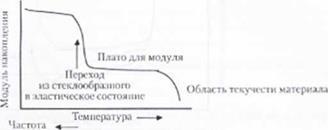

 Опубликовано в рубрике
Опубликовано в рубрике 