Приведенные выше рассуждения показываю!, что прямое измерение поверхностной энергии твердых тел представляет собой довольно трудную задачу. В современном исследовании процессов взаимодействия на поверхностях существует другой метол, позволяющий непосредственно оценить взаимодействия между поверхностями твердых тел. В данном методе используется устройство для анализа поверхностных сил (SFA) [22]. и анализ результатов эксперимента был выполнен Джонсоном. Кендаллом и Робертсом (Johnson Kendall-Roberts, JKR) (23). Правильное представление об основах теории./KR и эксперименты позволяют во многом понять основное физическое явление адгезии. Комплексное рассмотрение энергетического баланса, механики разрушения и механических свойств материалов играет определенную роль при экспериментальных исследованиях, а также при анализе результатов эксперимента.
На рис. 4.5 схематически показано соприкосновение двух сфер. Первым эту ситуацию проанализировал Герц [24). который принял допущение, что сферы абсолютно упругие и не имеют какой-либо адгезии. Герцу удалось доказать, что
(439)
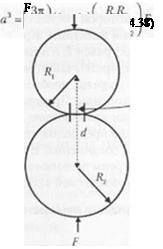
![]() Параметр v( — коэффициент Пуассона і-го материала; Е — модуль упругости при растяжении j-ro материала; /? — радиус кривизны і-го материала; F — усилие, приложенное к двум материалам, и а — радиус контакта между двумя сферами. Кроме того, теория Герца показывает, что расстояние между центрами двух сфер Л должно описываться уравнением
Параметр v( — коэффициент Пуассона і-го материала; Е — модуль упругости при растяжении j-ro материала; /? — радиус кривизны і-го материала; F — усилие, приложенное к двум материалам, и а — радиус контакта между двумя сферами. Кроме того, теория Герца показывает, что расстояние между центрами двух сфер Л должно описываться уравнением
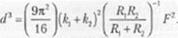
 |
(4.40)
Риг. 4.5. Лнлірамма, демонстрирующая огненной принцип анализа ll-pua. На рисунке показаны две упругие сферы, находящиеся в контакте. Также показаны радиусы кривизны и расстояние между двумя центрами
Па рис. 4.6 представлена схема ситуации, анализ которой выполнили Джонсон. Кендалл и Робертс. Эти исследователи установили, что усилие, необходимое для разделения двух контактирующих тел, не равно нулю, как принимал в своих рассуждениях Герц, и радиус контакта двух тел не соответствует значению, которое приведено в описанном выше уравнении Герца. Расстояния в уравнении также являются некорректными. Джонсон, Кендалл и Робертс предложили правильную гипотезу, свидетельствующую о том. что различие данных, полученных по уравнению Герца, от экспериментальных результатов является следствием влияния сил адгезии.
Метод оценки механизма контакта двух сфер при наличии сил адгезии, действующих между их поверхностями, иракгически аналогичен методу, который был рас-
|
F
|
{*ис.4.6. Схематическое изображение положения материалов, проанализированного ме толом JKR. Радиус контакта, представленный в уравнениях Герца, обозначен параметром а0, в то время как радиус контакта двух тел, для которых характерно адгезионное взаимодействие, имеет обозначение а,. Радиус кривизны показан на рис 4 5. Пунктирными линиями показано решение, соответствующее уравнениям Герца, сплошными линиями — ситуация, когда существует адгезионное взаимодействие между двумя телами
смотрен ранее в гл. 2 и 3 при анализе механики линейного упругого разрушения. Этот метод п|)едусматривает наличие баланса энергии. Другими словами, в данном случае анализ выполняют не относительно напряжений и деформации, как в случае анализа Роланда Рейснера для образцов с нахлесткой при испытаниях на сдвиг, но в первую очередь относительно энергий. Для представленной на рис. 4.6 системы очевидно, что общая энергия системы Ur состоит из т|х;х частей: механической потенциальной энергии і’и. потенциальной энергии упругодеі|>ормированііого тела Ut и поверхностной энергии в системе Vr Параметр Us просто представляет собой работу сил адгезии в случае сфер, изготовленных из различных материалов, находящихся н контакте друг с другом, и работу когезии в случае контактирующих между собой однородных материалов. Обратимся теперь к параметру механической потенциальной энергии. Для этого анализа необходимо рассмотреть рис. 4.7.
Сначала рассчитаем механическую потенциальную энергию в системе. Если к двум сферам прикладывается усилие /•’, и в результате воздействия этого усилия п|х>- исходит смешение /I.,, можно просто описать механическую потенциальную энергию в системе выражением Ffid., (точка 3 на рис. 4.7). Можно рассчитать энергию упругодеформированною тела, в первую очередь принимая, что с<|)сры приводятся в описываемый уравнением Герца контакт усилием F0. kotojxjc вызывает смешение Герца, представленное параметром dty Данная ситуация является таким случаем, когда отсутствуют поверхностные силы, и соответствует точке 1 на рис. 4.7 и радиусу а0 (см. рис. 4.6). Затем можно обратиться к условию существования поверхностных сил, приняв, что оно эквивалентно наличию какой-либо внешней силы Герца, приложенной к двум сферам. Далее существует ситуация в точке 2, для которой характерны усилие F,, смещение dt (рис. 4.7) и радиус я, (рис. 4.6). Точки 1 и 2 описывают не
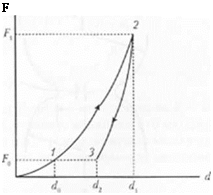 |
Рис 4.7. График зависимости усилие-смещение ;іля анализа механизмов контакта двух сфер при использовании принципа энергетического баланса
реальную, а главным образом виртуальную ситуацию и позволяют рассчитать энергию в системе. Затем введем некоторое менее строгое допущение в систему для того, чтобы экспериментально определить состояние в точке 3 (рис. 4.7). В этом случае общая энергия упругого взаимодействия в системе представляет собой количество энергии, необходимой для достижения точки 2, за вычетом энергии, требующейся для достижения точки 3. Энергию, необходимую для достижения точки 2, просто определить, так как выше было сделано допущение, что тело подчиняется механике Герца. Перестановкой членов в уравнении (4.40) можно определить d и затем, проинтегрировав d dh’от F — 0 до /•’ = Fv получаем
Рассчитать параметр Ui можно довольно и|хк-то, если известна взаимосвязь между F и d для «ненагруженной» кривой. Кривая нагрузка-деформация для такой ситуации была исследована Джонсоном [25] и описывается уравнением
![]() іші-L
іші-L
3 Ка.
|
15 1 3 F}’ |
что приводит к выражению
Это сложное алгебраическое выражение может быть использовано для определения взаимосвязи между /’, и Fa и. что более важно, между Fu и а(. І Ірн равновесном
состоянии (в данном случае являющемся частью энергетического баланса) получаем уравнение
Использовав это условие равновесия в уравнении для і’г находим
![]() f, = + 3VakR+JbWjRF’ + (3 W, лЛ)1.
f, = + 3VakR+JbWjRF’ + (3 W, лЛ)1.
Данное уравнение показывает, что кажущаяся сила Герца больше, чем реальная приложенная нагрузка, и что это увеличение силы происходит в |н*зультатс работы сил адгезии. Этот результат также может быть использован для того, чтобы предсказать другие особенности области контакта, когда принимают во внимание действие поверхност ных сил. Установлено, что радиус площади контакта оказывается больше, чем в случае площади контакта, описываемой уравнением Герца, и может быть представлен следующим уравнением:
![]() а’ F+2\nR^yjGW^Rh — t (3WtnR)’ ].
а’ F+2\nR^yjGW^Rh — t (3WtnR)’ ].
Анализ этот уравнения показывает, что в случае отсутствия приложенной нагрузки еще существует какой-то определенный радиус контакта, который не описывается уравнениями Герца, и который является одним из экспериментальных доказательств теории JKR. Кроме того, рассматривая уравнение для расчета радиуса контакта, находим, что если растягивающее усилие приложено к двум сферам (т. е. a-F), то радиус уменьшается до тех пор, пока не достигнет точки, кото|>ая описывается выражением
![]() F… = —W. xR.
F… = —W. xR.
JbK rs Л
 |
|
Альтернативный анализ механики двух находящихся в контакте упругих сфер был выполнен Могнсом и Барквинзом (26]. И данном случае к сферам не прикладывалась нагрузка и ситуацию моделировали как распространение трещины на границе раздела между двумя упругими сферами. Для рассматриваемого случая Могнсом и Барквинзом предложено следующее уравнение:
Обозначение ‘f>a использовано в уравнении (1.49) для того, чтобы показать, что этот параметр по своему существу аналогичен скорости освобождения энергии деформации, рассмотренной в гл. 2. В последнее время параметр (8 получил название «энергия адгезии», которая представляет собой присущую находящейся в контакте системе энергию деформации, обусловленной адгезией. Этот параметр будет ис пользоваться в дальнейшем в гл. 6 при обсуждении характера зависимости между теоретической силой адгезией и практической адгезией.
Можно образовать две упругие сферы и привести их в тесный контакт. К образцу прикладывают растягивающую нагрузку до полного разделения с«|к;р И данном случае величина усилия может быть измерена и непосредственно связана с работой сил адгезии. Нели оба находящихся в контакте тела материала представляют собой один и тот же материал, то Н’ — U’ — 2ys и уравнение (4.48) может быть использовано для непосредственного определения поверхностной энергии твердого тела.
Для прямою измерения поверхностной энергии твердых тел на основе теории JKR используют два типа оборудования. Первый прибор был описан JKR: схематическое изображение этого прибора представлено на рис. 4.8.
|
Рис. 1.8. Схема прибора. ия определения поверхностной анері ни. используя теориюJKIi |
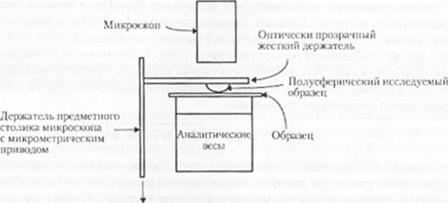
Этот прибор является удивительно простым. Образец должен быть оптически прозрачным и упругим пол действием рассматриваемых нагрузок. Вторая половина образца также может иметь сферическую <|юрму, однако наиболее часто она бывает плоской н на нес нанесено покрытие либо из тою же материала, что и полусфера, либо из другого исследуемою материала (одна сфера, находящаяся в контакте с другой п|>ерой. является аналогичной сфере, находящейся в контакте* с плоским образцом материала согласно допущению Дерягина (27). если радиус кривизны сферы больше площади измерения). Образец в виде полусферы наносят на оптически прозрачный жесткий держатель, который может совершать вертикальное перемещение. Усилие измеряют с помощью аналитических весов, а радиус контакта между сферой и плоской поверхностью определяют, используя оптический микроскоп. Уравнение (4.47) применяют для оценки ]>аботы сил адгезии между двумя материалами.
Наиболее часто используемым оборудованием для прямых измерений сил адгезии между поверхностями твердых тел является прибор для оценки поверхностных сил (5/54) (22]. Прибор был впервые описан Тейбором (28] и более глубоко проработан и использован Израелашвили [28] с сотр.: в аппаратуре SFA применены прямые механические методы измерения расстояний между поверхностями, величина которых составляет менее нескольких долей нм. а также механические методы измерения усилий между этими поверхностями. На рис. 4.9 приведена схема прибора для измерения поверхностных сил.
|
Оптическая,, система * К спектрометру
|
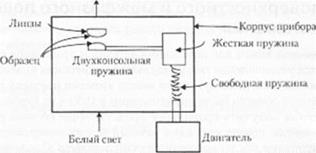
Л/с. 4.9 Схема прибора Израелатвилн для измерения поверхностных сил (SFA)
Прибор измеряет усилие НО отклонению ДВОЙНОЙ КОНСОЛИ определенной ЖССТКО* сти и с помощью интерферометрии позволяет определить расстояние между двумя поверхностями. Образцы должны быть почти плоскими на атомном уровне, тонкими (толщиной около 2 5 мкм) и оптически прозрачными. Обратную поверхность каждого образца серебрят для придания ему частично отражающих свойств. Затем образцы приклеивают к линзам. Линзы устанавливают в прибор таким образом, чтобы фокусы линз касались друг друга, образуя тем самым практически точечный контакт. І Іовсрхности образцов приводятся в тесное соприкосновение с помощью двигателя. Проходящий через образны белый свет позволяет измерять расстояние, разделяющее поверхности образцов. Когда образны находятся в непосредственной близости друг к другу, в спектрометре можно наблюдать интерфс]>енционные полосы. Эти полосы известны как «Полосы одинакового хроматического порядка» или FECO. Расстояние между полосами (которые наблюдаются в спект рометре) может быть использовано для оценки расстояния между поверхностями. Форма полос также соответствует форме поверхности линз.
Если поверхности образца не находятся в контакте, полосы FECO имеют приблизительно параболическую форму. На некотором расстоянии от разделенных поверхностей силы притяжения между поверхностями оказываются больше, чем сила отталкивания пружины, и образцы вступают в контакт. Если поверхности находятся в контакте, площадь контакта является плоской и часті, полос FECO соответствует форме поверхностей, расположенных вне зоны контакта. Теория JKR позволяет предсказать образование такой формы контактной области н экспериментальные исследования показывают справедливость такого предположения [30). После наступления состояния контакта может быть приложено усилие сжатия и уравнение (1.47) может быть использовано для определения работы сил адгезии между двумя поверхностями.
После того, как наступает состояние контакта, в качестве альтернативы может быть приложено растягивающее усилие и усилие, необходимое для удаления об — разнов из зоны контакта, может быть определено с помощью уравнения (4.48) При возможности должны быть выполнены оба измерения и полученные данные согласованы. Результаты экспериментов данного типа и их применение в области науки об адгезии рассматриваются в тл. 6.
 19 августа, 2015
19 августа, 2015  admin
admin 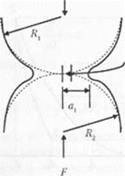
 Опубликовано в рубрике
Опубликовано в рубрике 