Лако-красочные материалы — производство

Mie applied the Maxwell equations to a model in which a plane wave front meets an optically isotropic sphere with refractive index n and absorption index к [1.33-1.36]. Integration gives the values of the absorption cross section Qa and the scattering cross section Qs; these dimensionless numbers relate the proportion of absorption

and scattering to the geometric diameter of the particle. The theory has provided useful insights into the effect of particle size on the color properties of pigments.

Scattering is considered first. Here, the crucial parameter a in the Qa and Qs for­mulae is a relative measure of particle size because it is proportional to the particle diameter D and is inversely proportional to the wavelength ё. At a constant wave­length ё and for various relative refractive indices n (i. e., relative to the binder, n = np/nB where np and nB are the refractive indices of the particle and binder, respec­tively), it gives the relationship between scattering and particle size (Figure 1.9) [1.34]. If, on the other hand, the particle size D is kept constant, a denotes the relationship between the scattering and the wavelength (l/ё replaces D on the abscissa of Figure 1.9). The well-marked maxima are typical, and their existence signifies

1. that an optimum particle size must exist with respect to lightening power [1.37], and

2. that for a given particle size, there must be a particular wavelength for maxi­mum light scattering [1.38].

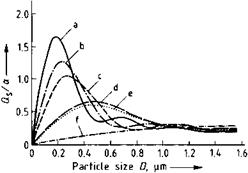Fig. 1.9 Scattering of white pigments as a function of particle size (ё = 550 nm). (a) Rutile; (b) anatase; (c) zinc sul­fide; (d) zinc oxide; (e) white lead; (f) barium sulfate.

The first relationship can be used to predict the optimum particle size of white pigments (Table 1.7). The second relationship explains, for example, how white pig­ments in gray color mixtures can produce colored undertones as a result of selective light scattering (see Section 1.3.2).

The consequences of Mie’s theory for absorption (i. e., for tinting strength) are now considered. Calculations from Mie’s theory, using the relative refractive index n and the absorption index к, are given in Figure 1.10 [1.39]. The parameter a on the abscissa can once more be taken as a relative measure of the particle size. The following conclusions may be drawn:

1. For very small particles, the absorption is independent of the particle size, and hence any further reduction in particle size does not produce additional absorption. 2

Fig. 1.10 Absorption as a function of particle size.

3. 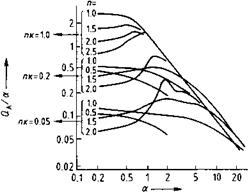Absorption values for large particles are approximately equal for all relative refractive indices n and absorption indices к, and decrease hyperbolically.

4. The top curve in Figure 1.10 applies to pigments with a high absorption index к and low refractive index n (e. g., carbon black) and shows that the optimal particle size lies below a given limit.

5. The lowest curve applies to pigments with a small absorption index к and high relative refractive index n, as is usually the case with inorganic pigments (e. g., red iron oxide). Here, there is a distinct maximum [1.16, 1.22].

The above relationships (Figure 1.10) show that the optical pigment properties depend on the particle size D and the complex refractive index n = n (1 — ік), which incorporates the real refractive index n and the absorption index к. As a result, the reflectance spectrum, and hence the color properties, of a pigment can be calculated if its complex refractive index, concentration, and particle size distribution are known [1.40]. Unfortunately, reliable values for the necessary optical constants (refractive index n and absorption index к) are often lacking. These two parameters generally

depend on the wavelength and, owing to the optical anisotropy of most pigments, on the illuminant and viewing direction. In pigments with a high absorption, the refractive index shows “anomalous dispersion”. Selected values of material of interest are given in Refs. [1.41, 1.42]. Applying these values it has to be remembered that they have been obtained from natural minerals found in the size necessary to make a measurement by ellipsometry possible. The results do not necessarily match the exact values in pigments. Unfortunately, no direct methods exist for determining n and к in colored inorganic pigments. A good review of the problems occurring when trying to simulate the behavior of pigments in paints with Mie-scattering can be found in e. g. Ref. [1.43]. Refractive indices of inorganic pigment materials are given at selected wavelengths in Tables 1.7 and 1.8. However, these values were measured on large crystals, and not on pigment particles.

1.3.2