It may be adequate in everyday life to think of a flat surface as the two-dimensional plane of Euclidean geometry. This, like the perfectly straight line with length but no breadth, is a
|
Figure 2 Fully hydrated calcite {1011} surface showing (top) rotation of surface carbonate groups with (bottom) bulk ordering below the surface (after Ref. 45). |
model constructed in our minds. In the present discussion it is necessary to recognize that the surfaces of science and technology depart from this idealization.
An atom or molecule within the bulk of a phase, surrounded by other atoms, is attracted in all directions. The asymmetry of the intermolecular force field as an interface is approached means that the surface molecules are more strongly attracted in one direction, usually towards the bulk. As a consequence, the density of molecules in the surface regions differs from that in the bulk. This perturbation may extend over many atomic spacings. Figure 2 gives the structure predicted by atomistic simulation techniques for a calcite (CaCO3) surface, and shows rotation of surface groups and adsorbed water [45].
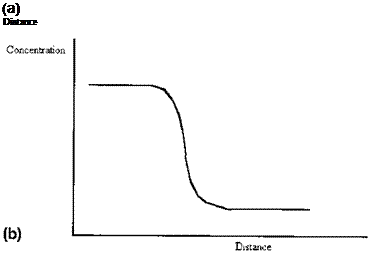
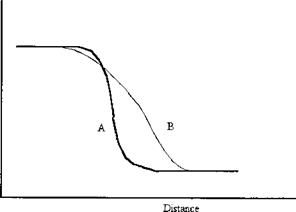
Even for an interface between two highly insoluble phases some interpenetration of molecules will occur, lowering the entropy. Liquids, and even solids, exert a vapor pressure. Thus the concentration profile across an interface is never sharp, there is always a finite and varying gradient (Fig. 3(b) cf. Fig. 3(a)). Further, where a multicomponent phase is concerned, there is in general no reason to suppose that the concentration profile of each component will be the same (Fig. 3(c)). Although it is sometimes convenient to speak of a surface as if it were defined by a plane, it is necessary to recognize that the positioning of the plane, for real materials, is arbitrary: it is a matter for convention.
Considerations of surface thermodynamic functions, especially of surface energy, are usually regarded as fundamental to an understanding of both the formation and the failure of adhesive bonds. A brief outline will be given of how these concepts are applied to smooth surfaces as a preliminary to describing their application to rough surfaces.

 |
|
|
|
|
|
|
In defining surface thermodynamic functions, the difficulty over the absence of a unique surface plane is circumvented by defining these functions in terms of surface excess— ‘‘total’’ minus ‘‘bulk’’ value of the property concerned [46,47]. Thus the Gibbs surface free energy is defined as
where A is the area of the surface, G is the total value of the Gibbs free energy in the system, and Gb is the value the total Gibbs free energy would have if all the constituent particles (atoms, molecules, etc.) were in the same state as they are in the bulk of the phase. It is because the local environment of molecules in or near the surface is different from that of those in the bulk (cf. Fig. 2), that there is an excess energy, the surface energy. In oversimplified terms, a surface can be thought of as being generated by breaking bonds along what becomes the surface. The energy to break these bonds is reflected in the surface energy.
Surface energies are associated with formation of the adhesive bond because they determine the extent to which, at equilibrium, a liquid adhesive will come into contact with a solid surface. This is reflected in the value of the contact angle, в, which is related to the surface energies (written, following common usage, as y) by Young’s equation [48]
ysv = ySL + yLV cos в (2)
where V refers to the vapor present in equilibrium with the solid (S) and liquid (L).
The energy change (per unit area) when liquid L spreads over the surface of solid S is called the spreading coefficient or spreading energy, S [48], and is necessarily related to the surface energies:
S = ySV — ySL — yLV (3)
Equations (2) and (3) enable the extent of contact between a liquid adhesive and a solid substrate to be gauged. Some consequences are shown in Table 1 where the concept of the ‘‘reduced spreading coefficient’’ S/yLV, employed by Padday [49], has been used to clarify the situation. As is readily seen, if S is positive, the liquid at equilibrium will be spread completely over the solid, but if S/yLV is less than — 2, spontaneous dewetting will occur.
Surface energies are also associated with failure of an adhesive bond, because failure involves forming new surfaces and the appropriate surface energies have to be provided.
|
Table 1 Contact Angle, в, and Spreading Coefficient for a Liquid on a Solid Surface. Comparison of Spreading Coefficient S for a Smooth Surface with S for a Surface of Roughness Factor r
aThese are in quotation marks because strictly 0° < в < 180°. |
The surface energy term may be the work of adhesion, WA, or the work of cohesion, WC, depending on whether the failure is adhesive or cohesive. For phases 1 and 2, these are defined as follows [49]:
WA = Y + Y2 — Yn (4)
Wc = 2y1 (5)
The practical adhesion, for example fracture energy G, will comprise a surface energy term G0(Wa or WC) to which must be added a term ф representing other energy absorbing processes—for example plastic deformation—which occur during fracture:
G = Gq + ф (6)
Usually is very much larger than G0. This is why practical fracture energies for adhesive joints are almost always orders of magnitude greater than work of adhesion or work of cohesion. However, a modest increase in G0 may result in a large increase in practical (measured) adhesion as and G0 are usually coupled. For some mechanically simple systems where is largely associated with viscoelastic loss, a multiplicative relation has been found:
G = Gq{1 + ф(с, T)}« G0<p(c, T) ()
where ф(с, T) is a temperature and rate dependent viscoelastic term [50,51]. In simple terms, stronger bonds (increased Gq) may lead to much larger increases in fracture energy because they allow much more bulk energy dissipation (increased ) during fracture.
 20 июня, 2015
20 июня, 2015  Malyar
Malyar 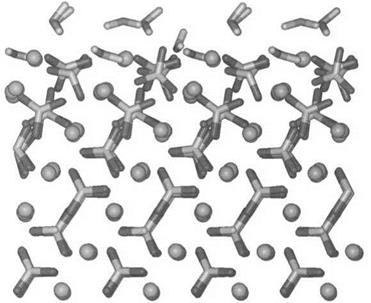
 Опубликовано в рубрике
Опубликовано в рубрике 