In a mean field approach, the interaction between one chain and all the other chains of the adsorbed layer is approximated by a mean field potential proportional to the local concentration U(z) = kTvc(z) and the average conformation of one chain is calculated in this potential. The conformation of one chain is characterized by the partition function
|
Figure 3 Two parallel plates bridged by end-adsorbed polymers. |
|
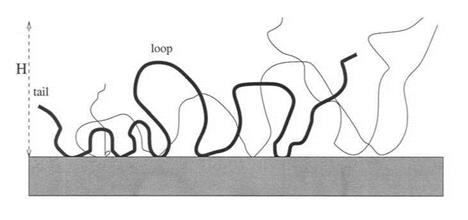
Figure 4 Structure of an adsorbed layer. Each chain is composed of two tails in the vicinity of the end points and forms loops on the surface. |
ZN(z) which is proportional to the number of conformations of a chain with one end point fixed [18,7] at a distance z from the surface; the partition function satisfies a diffusion-like equation
The interaction with the wall has a very short range and can be considered as a boundary condition to this equation on the surface (z = 0). The boundary condition is, in general, written as
where the adsorption length b is inversely proportional to the energy gain of a monomer upon adsorption. If the energy gain is of the order kT, the adsorption length is of the order of the monomer size. This equation for the adsorption of a polymer solution must then be made self-consistent by recalculating the local monomer concentration from the chain conformation. A very powerful and useful numerical scheme was introduced some time ago by Fleer et al. [5] who were the first to point out the importance of the distinction between monomers belonging to the tail and loop sections of the chains. This scheme has been applied to many experimental situations and, in particular, to the calculation of the interaction between surfaces that we discuss in this chapter. We will consider here the limit of polymers with a very large molecular weight for which an asymptotic analysis is possible. It has been checked explicitly that the numerical approach is consistent with this asymptotic analysis [23,24].
In order to calculate the chain partition function, it is convenient to decompose the partition function into two parts. The partition function of an adsorbed chain (a chain that has at least one monomer in contact with the surface) is the first order parameter j/(z) [25]. The partition function of a free chain (a chain that is nowhere in contact with the surface) is characterized by a second order parameter ‘(z). The two order parameters satisfy equations very similar to Eq. (3). If a monomer belongs to a loop, the two subchains starting from this monomer are adsorbed chains and the statistical weight associated with this monomer is proportional to t/r2(z). If a monomer belongs to a tail, the two subchains are a free chain and an adsorbed chain; the corresponding statistical weight is proportional to j/(z)'(z). By choosing a proper normalization of the partition function, the monomer concentration can be written as
c(z) — f2(z) + B f(z)'(z) (4)
where B is a constant. The mean field potential can then be expressed as a function of the two order parameters which makes the problem self-consistent. The constant B is calculated by noting that the chain end point concentration is ce(z) — Bt/r(z), and by writing the conservation of the end points (if the adsorbed layer contains Г monomers per unit area the total number of end points per unit area is 2Г/N). The first term in the monomer concentration (4) is the concentration of monomers belonging to loops and the second term is the concentration of monomers belonging to tails.
An explicit solution of these mean field equations shows that an adsorbed polymer layer has a double layer structure: close to the wall the concentration of monomers belonging to loops dominates and c(z) — a2/3vz2. Further away from the surface, the concentration of monomers belonging to tails dominates and c(z) — 10a2/3vz2. One can note that the scaling of the monomer concentration with the distance from the surface is
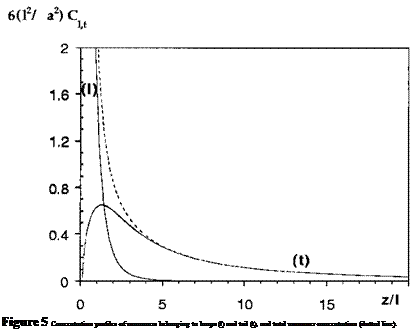 |
the same in the tail and loop regions, but that the prefactor is different. The crossover between the tail and the loop regions occurs at a distance 1 ~ N1/3. A plot of the loop and tail concentrations is given in Fig. 5.
The total thickness of the adsorbed layer is obtained by balancing the chemical potential of the chains in the adsorbed layer with that in the bulk. It is equal to
where cb is the bulk concentration and it is of the order of the bulk radius of gyration of the chains. The total number of adsorbed monomers per unit area is obtained by integration of the concentration profile and is equal to Г = a2/3vb in the limit of very long chains; it depends only very weakly on the chain molecular weight and on monomer concentration at moderate polymer density.
 27 июня, 2015
27 июня, 2015  Malyar
Malyar 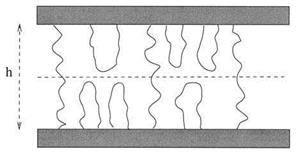
 Опубликовано в рубрике
Опубликовано в рубрике 