The equilibrium interaction between two parallel surfaces mediated by a polymer solution can be studied within the mean field approximation [34]. The polymer in the gap between the two surfaces is in equilibrium with a reservoir that fixes its chemical potential. One first determines the concentration profiles and then calculates the free energy. The interaction results from a competition between the osmotic repulsion and an attractive bridging contribution. The two contributions scale in the same way and one has to perform a complete calculation in order to determine the sign of the force. At large distances, when the two layers do not overlap, h > 2H, the force is exponentially small. At shorter distances, 1 < h < 2H, the force per unit area is repulsive and varies as
![]() 70kT a4 6v h4
70kT a4 6v h4
In this range of distances, only the tails are important and as in the case of the polymer brush the tails repel each other. The force is of the order of the osmotic pressure at the midplane between the two surfaces (z = h/2). At short distances b<h < 1 the force still varies as 1/h4 but it is attractive. In this range, the loops on both sides overlap to form bridges and the bridging attraction dominates. This equilibrium force can be measured only in cases of reversible adsorption; this in general is not the case for adsorption on solid surfaces but it could be the case for adsorption on a liquid-liquid interface.
As explained above, on a solid surface the adsorption is irreversible. We will treat here the irreversibility by assuming that the adsorbed amount 2Г in the gap between the surfaces remains constant. If the surfaces are saturated with polymer, that is if the adsor — bance is equal to its maximum value Г = a2/3vb, the force is repulsive at all distances; at
|
Figure 7 Force between two plates f as a function of the distance h between plates in a case of irreversible adsorption. The values of Г are indicated on the arrows. The plotted quantities are made dimensionless using the units defined in Ref. [35]; the unit length is the crossover distance 1. |
large distances it has the same dependence as in the equilibrium case, though with a higher numerical prefactor. If the surfaces are undersaturated, Г < a2/3vb, bridging becomes more important at short distances and the force is nonmonotonic, attractive at short distances due to bridging and repulsive at large distances due to the tails. Eventually, at lower values of Г, the force is attractive at all distances [35,36]. A plot of the force as a function of distance calculated from the mean field theory is displayed in Fig. 7. In the figure, for the smallest values of Г, the force is attractive at very short distances; this is not realistic as the dominant effect is the compression of a dense polymer layer. This is an artifact due to the virial expansion. A more realistic treatment including higher term in the virial series shows that at very short distances, the force is repulsive again. At intermediate values of Г, the force is thus repulsive then attractive then repulsive when the distance h decreases.
The scaling theory does not provide the sign of the force but only the scaling behavior as a function of the distance. It is reasonable to assume that the mean field theory does provide the correct qualitative variation of the force and that only the scaling behavior is not accurate. A simple scaling argument shows that in all the regimes where the mean field theory predicts a force varying as h“4, the force actually scales as f ~ h~3 [37].
There is a whole body of experiments on polymer mediated interactions between solid surfaces performed using the surface forces apparatus (mostly by the group of J. Klein [38], but also by other techniques. The theoretical picture presented here is in good agreement with most of the results.
 27 июня, 2015
27 июня, 2015  Malyar
Malyar 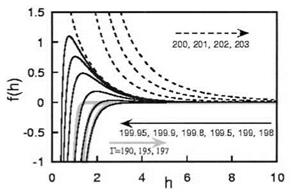
 Опубликовано в рубрике
Опубликовано в рубрике 