The interaction between two surfaces each carrying a grafted polymer layer of thickness H is repulsive [15]. If the distance h between the surfaces is larger than 2H, the polymer layers do not overlap and the force between the surfaces owing to the polymer vanishes. If the distance h is smaller than 2H, the two brushes interact. It can be shown that they do not interpenetrate but that they compress. The repulsive force is then due to the osmotic pressure opposing the compression. In the Alexander-de Gennes model, the concentration in the compressed layers is c = 2a/h and the osmotic pressure, n, which is the force per unit area between the surfaces is [6]
n ~ kT(fT (2)
We have considered in this expression the polymer inside the layers as a semidilute solution and used the scaling expression for the osmotic pressure [18]. Note that we ignore here the variation of the monomer concentration at the edge of the grafted layer. Equation (2) thus overestimates the interaction between the two grafted layers when they are close to overlapping, h « 2H.
Bridging by grafted polymer chains can be induced by considering an irreversibly grafted polymer layer and by allowing the free end points to adsorb, with an adsorption energy 8 per adsorbed end point [19], on a surface parallel to the grafting surface. The chains with adsorbed ends form bridges between the two surfaces. If the adsorbing surface is free with no applied force, the fraction of chains making bridges increases as a function of the reduced adsorption energy 9r = 9/д from zero to one. For most practical cases the chemical potential of the chains in a free brush is much larger than kT and the reduced adsorption energy is small which implies that the number of bridges is small. This is due to the fact that the end points of the chains are buried inside the layer and that in order to adsorb them one must stretch the chains to the adsorbing surface which costs elastic energy. A detailed calculation with the self-consistent field model shows that the fraction of chains forming bridges ^ increases linearly with 8r. The grafted layer also shrinks upon bridging.
If a force is applied to the adsorbing surface, the fraction of bridges increases under compression (the repulsive osmotic force then dominates over the attractive bridging force); eventually, if the compression force is large enough, all the chains form bridges. Under extension, the number of bridges decreases (the bridging force dominates over the osmotic force) and eventually the system becomes unstable if the force is larger than a critical force. The interaction energy U between the two surfaces is plotted as a function of the distance h between the surfaces in Fig. 2; the reduced variables are Fr = U/стд and dr = h/H. The curve has been calculated using the self-consistent field theory for a reduced attraction energy Sr = 0.2. The equilibrium position is at the minimum of the curve (zero force); the critical force where the system breaks under extension is at the inflection point (maximum force) and the region with a downwards curvature is unstable; the point of complete bridging (^ = 1) is indicated by the arrow. These results give a rather good description of experiments performed with polymer chains grafted on a sphere glued onto the tip of an atomic force microscope [20].
Another system where bridging is observed is a slab between two identical parallel solid plates with polymer chains that can adsorb by their end points on both surfaces. In the limit where the graft energy is large all end points are adsorbed and the slab is formed by loops on either plate and bridges between the two plates as sketched in Fig. 3. In this case also, the fraction of bridges at equilibrium has been found to be very low ^ ~ (<cN6=5a2)—2=3 [21,22]. The interaction energy is repulsive at distances smaller than the contact distance h = 2H and is attractive at larger distances. The equilibrium position is slightly shifted with respect to the contact distance; the interaction energy at the equilibrium position Umin ~ —кТац corresponds to an attractive interaction energy of kT per bridge.
|
Figure 2 Reduced interaction energy between surfaces Fr as a function of distance between the surfaces dr for a bridging brush. |
 27 июня, 2015
27 июня, 2015  Malyar
Malyar 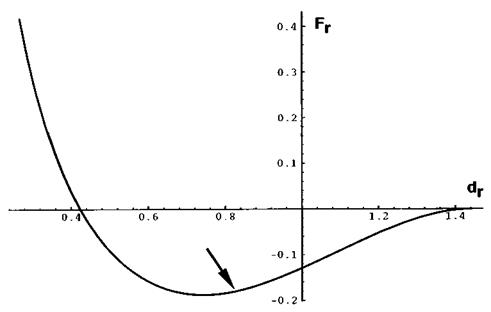
 Опубликовано в рубрике
Опубликовано в рубрике 