Лако-красочные материалы — производство

The diffusion theory of adhesion is based on the assumption that the adhesion strength of polymers to themselves (autohesion) or to each other is due to mutual diffusion (inter­diffusion) of macromolecules across the interface, thus creating an interphase. Such a mechanism, mainly supported by Voyutskii [71], implies that the macromolecular chains or chain segments are sufficiently mobile and mutually soluble. This is of great importance for many adhesion problems, such as healing and welding processes. Therefore, if inter­diffusion phenomena are involved, the joint strength should depend on different factors, such as contact time, temperature, nature and molecular weight of polymers, and so on. Actually, such dependences are experimentally observed for many polymer-polymer junc­tions. Vasenin [72] has developed, from Fick’s first law, a quantitative model for the diffusion theory that correlates the amount of material w diffusing in a given x direction across a plane of unit area to the concentration gradient dc/dx and the time t:

3c

3w = —Df 3t —— (20)

3x

where Df is the diffusion coefficient. To estimate the depth of penetration of the molecules that interdiffused into the junction region during the time of contact tc, Vasenin assumed that the variation of the diffusion coefficient with time is of the form Ddt~fi, where Dd is a constant characterizing the mobility of the polymer chains and is on the order of 0.5. Therefore, it is possible to deduce the depth of penetration lp as well as the number Nc of chains crossing the interface, which are given by

lp — k {nDdtxJ1)’l/1

‘2Np 2/3 ~M )

where k is a constant, N is Avogadro’s number, and p and M are, respectively, the density and the molecular weight of the polymer. Finally, Vasenin assumed that the measured peel energy G was proportional to both the depth of penetration and the number of chains crossing the interface between the adhesive and the substrate. From Eqs. (21) and (22), G becomes

where K is a constant that depends on molecular characteristics of the polymers in contact, Experimental results and theoretical predictions from Eq. (23) were found [72] in very good agreement in the case of junctions between polyisobutylenes of different molecular weights. In particular, the dependence of G on t/A and M_2/3 was clearly evidenced.

One important criticism of the model proposed by Vasenin is that the energy dis­sipated viscoelastically or plastically during peel measurements does not appear in Eq. (23). Nevertheless, in his work, the values of coefficients K and Dd are not theoretically quanti­fied but determined only by fitting. Therefore, it can be assumed that the contribution of hysteretic losses to the peel energy is implicitly included in these constants.

In fact, the major scientific aspect of interdiffusion phenomena is concerned with the dynamics of polymer chains in the interfacial region. Recently, the fundamental under­standing of the molecular dynamics of entangled polymers has advanced significantly due to the theoretical approach proposed by de Gennes [73], extended later by Doi and Edwards [74] and Graessley [75]. This new approach stems from the idea that the chains cannot pass through each other in a concentrated polymer solution, a melt, or a solid polymer. Therefore, a chain with a random coil conformation is trapped in an environment of fixed obstacles. This constraint confines each chain inside a tube. De Gennes has analyzed the motion, limited mainly to effective one-dimensional diffusion along a given path, of a polymer chain subjected to such a confinement. He described this type of motion as wormlike and gave it the name reptation. The reptation relaxation time r associated with the movement of the center of gravity of the entire chain through the polymer was found to vary with the molecular weight M as M3. Moreover, the diffusion coefficient D, which defines the diffusion of the center of mass of the chain, takes the form D — M“2.

One of the most important and useful applications of the reptation concept concerns crack healing, which is primarily the result of the diffusion of macromolecules across the interface. This healing process was studied particularly by Kausch and co-workers [76]. The problem of healing is to correlate the macroscopic strength measurements to the microscopic description of motion. The difference between self-diffusion phenomena in the bulk polymer and healing is that the polymer chains in the former case move over

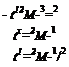distances many times larger than their gyration radii, whereas in the latter case, healing is essentially complete in terms of joint strength in the time that a macromolecule initially close to the interface needs to move about halfway across this interface. This problem was analyzed by several authors, who have considered that the healing process is controlled by different factors, such as (1) the number of bridges across the interface for de Gennes [77], (2) the crossing density of molecular contacts or bridges for Prager and Tirrell [78], (3) the center-of-mass Fickian interdiffusion distance for Jud et al. [76], and (4) the monomer segment interpenetration distance for Kim and Wool [79]. The resulting scaling laws for the fracture energy versus time t during healing are the following:

If there are some differences in the exponent of the molecular weight in these expressions, all the approaches agree with the dependence of G on the square root of healing time, such a dependence having been clearly evidenced experimentally for poly(methyl methacrylate) polymer, for example [76], in contradiction with Vasenin’s model.

Finally, it can be concluded that diffusion phenomena do actually contribute greatly to the adhesive strength in many cases involving polymer-polymer junctions. Nevertheless, the interdiffusion of macromolecular chains requires both polymers to be sufficiently soluble and the chains to possess a sufficient mobility. These conditions are obviously fulfilled for autohesion, healing, or welding of identical polymers processes. However, diffusion can become a most unlikely mechanism if the polymers are not or only slightly soluble, if they are highly cross-linked or crystalline, or put in contact at temperatures far below their glass transition temperature. Nevertheless, in the case of junctions between two immiscible polymers, the interface could be strengthened by the presence of a diblock copolymer, in which each molecule consists of a block of the first polymer bonded to a block of the second polymer, or each of the two blocks is miscible with one of the polymers. The copolymer molecules concentrate generally at the interface and each block diffuses or ‘‘dissolves’’ into the corresponding polymer. Therefore, the improvement in joint strength can also be related to an interdiffusion process. When the molecular weight M of each block of the copolymer is inferior to the critical entanglement weight Me for which entanglements of chains just occur in the polymer, the adhesion strength could be interpreted in terms of the suction mechanism described in Section II. D. On the contrary, when M > Me, the failure of the joint generally requires the rupture of the copolymer chains. The latter phenomenon (i. e., chain scission or more precisely rupture of chemical bonds) is analyzed in the next section.