As given in Eq. (1), the measurement of crack length can be avoided by tapering the specimen, such that dC/da is a constant. Extensive studies of compliance rate change of
|
Figure 8 Geometry of the wood-wood TDCB specimen for calibration study. |
|
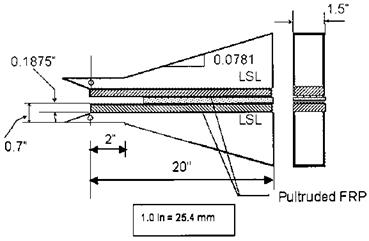
Figure 9 Geometry of the FRP-FRP TDCB specimen for calibration study. |
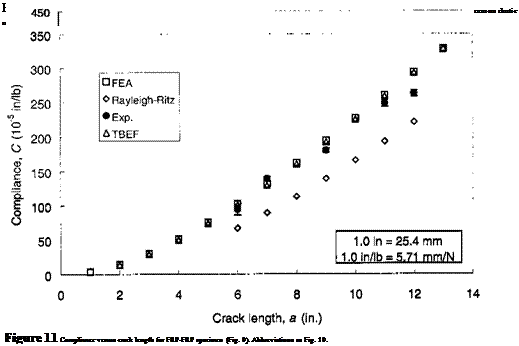
TDCB specimens with hybrid interface bonds are given by Davalos et al. [12] and Qiao et al. [13]. The linearity of the compliance-crack length relationship of the specimen is verified by both the Rayleigh-Ritz method and finite element analysis. An experimental compliance calibration program for specimens with wood-wood (Fig. 8) and FRP — FRP (Fig. 9) bonded interfaces was carried out. In the Rayleigh-Ritz method [8], the cracked tapered portion of the specimen (Fig. 6) was modeled as a cantilever beam by assuming no displacement and rotation at the crack tip; thus, the effect of crack tip deformation was ignored. As a result, this method may significantly underestimate the compliance (C), and even compliance rate change (dC/da), values of the specimen, as shown by the large differences [12] when compared to finite element analyses and experimental data (see Figs. 10 and 11 for wood-wood and FRP-FRP bonded interfaces, respectively). Later, a modified Rayleigh-Ritz method [15] was developed, in which higher-order shape functions for deflection and rotation were introduced to
replace the quadratic shape functions used before [8,12]; however, the accuracy of the model was only slightly improved, since cracktip deformations were not permitted. The same problem of underestimating the compliance was also observed in a study using constant cross section DCB specimens [16].
|
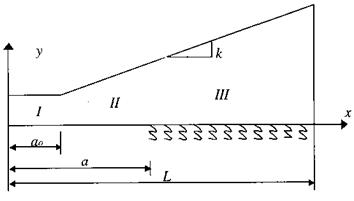
Figure 12 Modeling of TDCB specimen on an elastic foundation (after Ref. 13). |
Recently, a modified beam theory [13] was developed to predict the compliance rate change of TDCB specimens for mode-I fracture of hybrid interface bonds. The analytical model treats the uncracked region of the specimen as a tapered beam on a generalized elastic foundation (Fig. 12), and the effect of crack tip deformation is incorporated in the formulation. A closed-form solution is obtained to compute the compliance and compliance versus crack length rate change. The tapered beam on elastic foundation (TBEF) model is verified with finite element analyses and experimental calibration data for wood-wood and FRP-FRP bonded interfaces (Figs. 10 and 11), and good agreements of compliance and compliance rate change are achieved for specified crack length ranges, for which a linear relation of compliance versus crack length is obtained, which can be used with experimental critical fracture loads to determine the respective critical strain energy release rate or fracture toughness of interface bonds. The analytical TBEF model, which accounts for the crack tip deformation, can be efficiently and accurately used for compliance and compliance rate change predictions of TDCB specimens and to reduce the experimental calibration effort that is often necessary in fracture studies. Moreover, the constant compliance rate change obtained for linear-slope TDCB specimens can be applied with confidence in mode-I fracture tests of hybrid material interface bonds.
 15 июля, 2015
15 июля, 2015  Malyar
Malyar 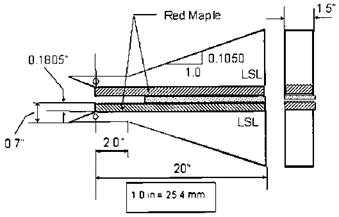
 Опубликовано в рубрике
Опубликовано в рубрике 