The molecular weight of an adhesive is of prime importance in its preparation, application, and performance. The effect of molecular weight on the tensile strength or bonding power of an adhesive is illustrated in Fig. 1. At very low molecular weights, the ultimate tensile
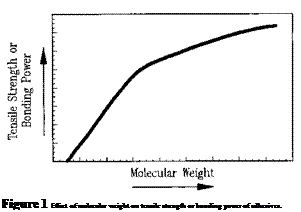 |
stress is near zero. As the molecular weight increases, the tensile strength rapidly increases, then gradually levels off. Hence, the useful bonding and mechanical properties of an adhesive are heavily dependent on its molecular weight. Normally, bonding power does not begin to develop in adhesives until a minimum molecular weight above 5,000 is achieved. Above that size, there is a rapid increase in the mechanical performance of adhesives as their molecular weights increase.
For analysis or characterization of adhesives, the first step is to determine the molecular weight or degree of polymerization. The molecular weights of adhesives can be determined by chemical or physical methods of functional group analysis or by measurement of the colligative properties, light scattering, ultracentrifugation, or dilute solution viscosity [1]. With the exception of some types of end-group analysis, all molecular weight methods require dissolution of the adhesive. This requirement is sometimes difficult to meet, particularly for very-high-molecular-weight or cross-linked adhesives. Hence, normally the average molecular weight is a property that can be measured only for linear and branched adhesives.
Unlike low-molecular-weight compounds where the molecular weight in the sample is uniform, polymer samples are usually polydisperse. They are composed of polymer chains of varying length and hence exhibit a distribution of molecular weights. Therefore, in expressing polymer molecular weights, various average expressions are used. These averages are defined in terms of the molecular weight M, and the number of moles n, or the weight w, of the component molecules by the following equations:
Number-average molecular weight:
Weight-average molecular weight:
![]() M _ E”Ml_ PWjMj w E n, Mi £ Wi
M _ E”Ml_ PWjMj w E n, Mi £ Wi
Z-average molecular weight:
![]() E”,-m?_ EwjM2 E ”iM2 E WiMi
E”,-m?_ EwjM2 E ”iM2 E WiMi
(Z+ 1)-average molecular weight:
![]() P n, Mi P wiMf
P n, Mi P wiMf
Viscosity-average molecular weight:
|
|||
|
|
Equation (5) is an important practical molecular weight average derived from viscometry. In order to calculate this average, the exponent a of the Mark-Houwink relationship relating intrinsic viscosity [p] to molecular weight must be known:
[p] = km (6)
where K and a are the characteristic parameters predominantly determined by the combination of polymer and solvent at a constant temperature. Extensive tables of constants K and a are available in the literature [2].
A typical molecular weight distribution (MWD) is depicted in Fig. 2. The Mn, Mv, Mw, Mz, and Mz+1 are labeled. It is obvious that
Mn < Mv < Mw < Mz < Mz+1 (7)
It is clear from these equations that for Mw, Mz, and Mz+1 the molecules of greater mass contribute more to the average than do less massive molecules. Conversely, Mn is very sensitive to the presence of low-molecular-weight tails. In the study of polymerization kinetics, Mn is a critical parameter. The glass transition temperature (Tg) of an adhesive is also particularly sensitive to low-molecular-weight species. Knowledge of Mn is also necessary for evaluating the level of functionalization in adhesives with specific end groups. In studying rheology, various average molecular weights and the shape and breadth of the distribution are important. Polydispersity ratios such as Mw/Mn and Mz/ Mw can give some insight into the latter problem. Adhesion, toughness, tensile strength, brittleness, and environmental stress-crack resistance are a few of the many properties affected by the MWD. For many adhesives, a narrower molecular distribution yields
|
better properties. An elegant way of determining the MWD is by gel permeation chromatography (GPC) or size-exclusion chromatography (SEC).
 10 июля, 2015
10 июля, 2015  Malyar
Malyar 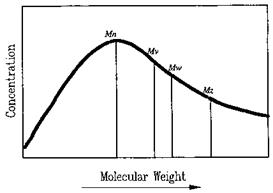
 Опубликовано в рубрике
Опубликовано в рубрике 