Лако-красочные материалы — производство

Different molecular mechanics systems and programs exist. There are programs that allow simultaneous variation of bonds and bond angles as well as allowing bond rotation, and there are programs in which instead all the covalent bond lengths and bond angles between covalently bonded atoms are fixed to specific values without allowance for their adjust­ment or modification during computation. It cannot be said that one system is better than the other as either of the two systems can be more apt at resolving a particular problem: it might then be necessary to choose the system according to the problem at hand.

The first type of program, based on an unconstrained force field approach is more comprehensive but suffers from the limitation of the size of molecules that can be inves­tigated due to the extent of computations needed. It is thus very apt for the study of smaller molecules or systems of molecules up to 40-60 atoms, but this limitation is also fictitious because it really depends on the capacity and calculation rate of the computer used. Such unconstrained force field programs tend to suffer furthermore from the pro­blem that the automatic search for the minimum of energy might lead the program to minimize on a local rather than total minimum, and if particular attention is not exercised completely false results can be obtained (the ‘‘black-box’’ syndrome).

The second type of program, based on a constrained force field approach, is gen­erally taken to render computation more rapid. It is then particularly useful when big molecules, such as polymers are involved. All these programs are based on the finding that conformational studies in the field of biological macromolecules have shown that the conformational energy of a molecule can be represented with accuracy even when bond lengths and angles between covalently bonded atoms are prefixed [1], and is represented by a sum of four types of contributions namely

Etot = EvdW + EH-bond + Eele + Etor C1)

Etot represents the total conformational energy of the molecule as a function of all the internal angles of rotation. EvdW represents the contribution to the total energy due to
van der Waals interactions between all the couples of unlinked atoms whose relative position depends on one or more internal bond rotational angles (ф°, ф°) (in degrees). This contribution can be expressed by Buckingham-type functions

EvdW — ^ ‘ [ay exp( bijrij) cijrj ] (2)

ij

where the coefficients a, b, and c depend on the couple i, j of atoms, or by Lennard-Jones — type functions

ij

Both types of functions are commonly used. Several sets of a, b, c, and d, coefficients are available [1-3]. Equally good results can be obtained using Lennard-Jones-type functions alone or Buckingham-type functions alone or mixtures of Lennard-Jones and Buckingham functions [4]. The attraction coefficients c/ in these expressions are generally but not always calculated with the formula of Slater and Kirkwood [5]:

where a, and о/ are the values of the polarizability of the atoms i and j, and Ni and Nj are the numbers of effective electrons, respectively.

In Eq. (2), b, j is fixed to a constant value [1,6-10] and a, j is determined by imposing the minimum at the distance that is the sum of the van der Waals radii of the atoms or groups considered [1,6-10]. The van der Waals interactions are always calculated here as the sum of the single interactions between each couple of unlinked atoms.

Eele describes the electrostatic contribution to the total energy. Dipolar momenta are here expressed, in the so-called monopolar approximation, by means of partial charges the values of which are fixed in such a manner as to reproduce the dipolar momenta of both bonds as well as the total dipolar momentum. Using partial charges, the dipolar interac­tions can be calculated with a Coulomb-type law of the form Eele — £ j — (q, #,)/(£ rj where qi and qj are the charges of the two atoms i and j, r j is the distance between i and j and є is the dielectric constant.

Etor describes the contribution to the total energy due to hindered rotation around skeletal bonds. The formulas generally used for the torsional potentials are those of Brant and Flory [2,6-10] where the torsional barriers used can be of different values [2,6-10]. It is necessary to point out, however, the limiting condition that must be imposed on the rotational degrees of freedom. Rotations around bonds that have very high torsional barriers (C—C, C—O), and single bonds between them affected by their conjugation, as in the case of polypeptides, must not be considered [11].

EH. bond represents the hydrogen bond (H-bond) contribution between couples of noncovalently bonded atoms. Several functions, even very simplified and empirical ones, have been used, and often with good success. The H-bond, however, is at best a difficult interaction to describe through a function which is capable of both giving good results while really taking into account the physicochemical reality of the interaction. It is for this reason that there is a multitude of empirical simplified functions for its calculation. Where the H-bond is of little or no importance often the molecular mechanics calculations are just done on the basis of only the van der Waals interactions (and not with bad results, as in the earlier days of protein structure refinement). In systems in which the H-bond

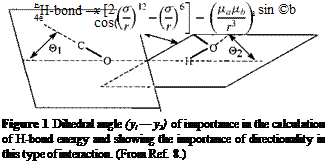contribution is important or determining to the results it is better to use a more compli­cated but more comprehensive function proposed by Stockmayer which has already been found to give very representative results in polypeptide sequences [ii] and in cellulose systems [12]:

У0)]

which takes into consideration the angular dependence of the H-bond. The first term in Eq. (5) describes the interaction between the hydrogen atom and the oxygen atom parti­cipating in the H-bond, and it is nothing else than a Lennard-Jones potential with the expression in simplified form. The second term describes the H-bond as an electrostatic interaction between two point-like dipoles of magnitudes да and дь centered on the oxygen and hydrogen atoms. The directional character of the H-bond is assured by the angular dependence of this function, and ©a and ©b are the angles that the C-O and O-H bonds form with the C-O—H-O segment linking the hydrogen and oxygen atoms (Fig. i). The value (ya — yb) (in degrees) is the angle between the planes containing the H-bond and the O-H and C-O bonds (Fig. 1). The e, a, and д are obtained by minimizing the first term of Eq. (5) at the van der Waals distance between the hydrogen and oxygen atoms, and the whole function at a H-bond distance of 2.85 A with aligned C-O and O-H bonds.

Also in many of the unconstrained force field type programs today similar expres­sions for the H-bond based on a Lennard-Jones first term as above or a Buckingham first term [13] followed by a term describing the dipolar and angular dependence of the H-bond are used. However, there are also a number of programs in which the H-bond is described just as a Buckingham function without any consideration being taken of the directionality of the H-bond, or even by simpler expressions. There is nothing very wrong with these simplified approaches in cases where the H-bond is not of fundamental importance to the study, but they cannot be used reliably in cases where the H-bond is of determining importance.