Contrary to the generalized approach already presented, models describing the adhesion between a polymer well defined at a molecular level and another, equally molecularly well-defined substrate also exist. These are models in which molecular mechanics and dynamics are applied in their more accepted role described in the Introduction. It must be realized that such models derive from a need different from what has prompted the development of the generalized models already described. They stem from the need to solve some applied problem of adhesion or to upgrade the performance of some adhesive systems in situations where the use of an experimental method would take too long, or is not able to give any clear results. It is for this reason that such models need to use the most precise and well-defined information possible or available on the molecules involved as well as using the sets of potential functions which describe in the most accurately conceptual manner the molecular behavior of the chemical species involved: all the research work that uses this approach is then applied to ‘‘real’’ case, not to idealized models, and is of considerable sophistication. Furthermore, all this type of research work is most commonly supported by direct or indirect experimental results which prove that molecular mechanics predicted well the improvements that needed to be implemented to upgrade adhesion or to upgrade an adhesive system. Notwithstanding their applied use, the sophistication of such a type of an approach has yielded very interesting results on the fundamental side of the science of adhesion and of the interface and it offers considerable promise and opportunities for more progress in the future.
The first of such studies [8] appeared in 1987 and thus preceded by a couple of years the first of the generalized approach studies [22]. It concerned the adhesion of phenol — formaldehyde (PF) polycondensates and resins to cellulose, hence to wood. It was followed later by other studies on the adhesion to crystalline and amorphous cellulose of urea-formaldehyde (UF) resins [7], of more complex PF oligomers [10], of water [29,30], of chromates [31], and finally of the more complex case of ternary systems in which two interfaces exist, namely in the situation of adhesion to cellulose and wood of an acrylic undercoat composed of a photopolymerizable primer onto which was superimposed an alkyd/polyester varnish [32,33]. The molecular mechanics algorithms used for all these studies were those already presented at the beginning of this chapter. The only difference was that for just the last of the studies mentioned the negligible importance of H-bonding to that particular system led to disregarding it in the calculations. Before the first of these studies, the understanding of the phenomenon of adhesion between a well-defined pair of adhesive and adherend had never been attempted by means of calculation of all the values of secondary interactions between the non covalently bonded atoms of the two molecules involved. This approach was rendered possible by the codification, again by molecular mechanics (or conformational analysis, as this technique was known in earlier days) from the data of earlier x-ray diffraction studies, of the spatial conformation of native crystalline cellulose (or cellulose I) [12], of the several mixed conformations possible for amorphous cellulose [12], and also of PF oligomers [34].
This initial molecular mechanics calculation was limited to the interaction with crystalline cellulose I of all the three possible PF dimers in which a methylene bridge links two phenol nuclei ortho-ortho, para-para and ortho-para. As not much was known as to how the system would react the investigation was very extensive. As cellulose constitutes as much as 50% of wood, where its percentage crystallinity is as high as 70%, this study also inferred applicability to a wood substrate. As even dried wood always contains a certain amount of water the influence of the water was taken into account by introducing into the calculations the effect of a parameter related to the dielectric constant of water.
The results obtained clearly indicated that adhesion of PF resins to cellulose was easily explained as a surface adsorption mechanism, a fact which, while very accepted today, was not evident in the wood gluing field and in the literature up to that time. This results also indicated that the interaction of the PF dimers with cellulose on all possible sites was more attractive than the average attraction by the cellulose molecule for the sorption of water molecules. In a few cases only, the interaction of water molecules with the few strongest sorption sites of cellulose was more attractive than that of PF dimers. This implied that in general even for the more difficult to wet crystalline cellulose the PF dimers, and by inference also higher PF oligomers, were likely to displace water to adhere to the cellulose surface. This was an important findings as it did show for the first time by numerical values that in wood bonding the adhesion of the polymer resin to the wood must be considerably better than the adhesion of water molecules to the wood. It is of importance first for ‘‘grip’’ by the adhesive of the substrate surface and secondly, in the cured adhesive state, in partly determining the level of resistance to water attack of the interfacial bond between adhesive and adherend. This result added a new dimension to the well-known water and weather resistance of PF-bonded lignocellulosic materials: it is not only due to the imperviousness to water of the cured PF resin itself, as believed up to then, but also to the imperviousness to water of the adhesive/adherend interfacial bond, a bond exclusively formed through secondary forces. A further deduction, with some applied inference, from the results was that a PF resin used to impregnate wood was likely to depress the water sorption isotherm of both wood and cellulose according to the number of substrate sorption sites which, on curing, have been denied to water, a deduction later confirmed experimentally.
The most important result, however, was that there were significant differences in the values of minimum total energy in the interaction of the three PF dimers with cellulose. It was possibly the more important conclusion, because it also had the more immediate industrial application. The ortho-ortho and ortho-para dimers had much greater average relative Etot of interaction with the cellulose surface than the para-para dimer. In general the distribution of the methylene linkage in standard commercial PF resins at that time indicated a higher proportion of the ortho-para and para-para linkage over the orthoortho linkages. Experimental results confirmed this finding [35]. Maximization of the proportions of ortho-ortho and ortho-para linkages and decrease of the relative proportion of the para-para coupling is easily obtained in PF resin manufacturing by the addition of ortho-orientating additives [37-40]. As a consequence, the adhesion and performance improvement caused by a shift in the relative proportions of methylene bridge coupling renders possible the reduction by about 10% of the quantity of PF adhesive resins used in a product such as wood particleboard, at parity of performance. Alternatively, it does improve the performance at parity of quantity: not bad results if one considers that approximately 2 million tons of PF resins are used for wood bonding each year. It is not claimed here that the molecular mechanics result converted the PF resins industry to maximize ortho-coupling, but the theoretical justification it offered contributed to greatly accelerating the already existing empirical trend in such a direction. Maximization of ortho-coupling in commercial PF resins is now a much more common practice. Further confirmation of this was later obtained by studies of dynamic, differential, and competitive adsorption [9] which will be discussed in the next section of this chapter.
The findings also contributed to the visualization of the conformation of minimum energy of a resin on a substrate: the equivalent of a static, schematic photograph of the conformation of the two molecules at the interface. An example of this is shown in Fig. 2. It also contributed to the understanding, although this came from later work [7], that not only the energy at the interface but also the conformation of minimum energy of a molecule on a substrate was quite different from the conformation of minimum energy of the same molecule when alone, or when on a different substrate. This was confirmed later by x-ray studies determining the degree and/or lack of crystallinity of hardened UF resins in the presence or absence of cellulose [41]. It is also for this reason that idealized models are limited to never being able to complete with ‘‘real’’ models to solve adhesion problems.
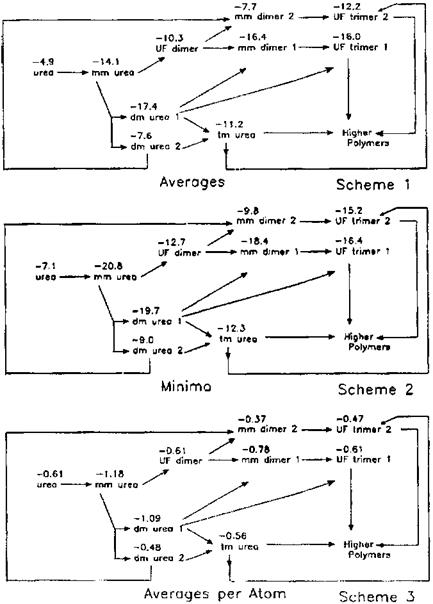
Further molecular mechanics investigations in the same direction but for UF resins also followed, with equally interesting results. In these the efficiency of resin adhesion to both amorphous and crystalline celluloses was computed by following the synthesis of the resin. This was achieved by calculating by molecular mechanics the adhesive/adherend interactions with the two types of cellulose for each isomeride produced through the reaction of urea with formaldehyde. This was done up to the level of trimer. The adhesive/adherend interactions were calculated for urea, monomethylene diureas,
|
Figure 2 Example of planar projection of one of the configurations of an ortho-para PF dimmer on the surface of a schematic cellulose crystallite showing a phenolic dimmer (a dihydroxy diphenyl methane) conformation of minimal energy and main dimer-cellulose hydrogen bonding. (From Ref. 8.) |
and dimethylene triureas, and their mono-methylolated, dimethylolated and trimethylo — lated species [6,7]. All the results found correspondence in already existing experimental results [42-44]. It was found, for example, that the lack of water — and weather-resistance of lignocellulosic materials bonded with UF resins did not appear to be due, to any large extent, to failure of their adhesion to cellulose. However, contrary to the case of PF resins exposed above, failure in the presence of water of UF resins to adhere to cellulose was also found to be only a minor contributory factor to their lack of water resistance. This confirmed that the lability to water attack of UF resins resided mainly in the hydrolysis of their amidomethylenic bond, a fact since confirmed experimentally. More important is the finding, later confirmed by x-ray diffraction [41], that when UF resins are interacting with cellulose some of the conformations that would be forbidden when the UF resin is cured alone become possible and are allowed. This same experimental study also confirmed that the secondary forces binding together linear chains, not cross-linked, of UF oligomers with cellulose were stronger than the intermolecular forces between the UF oligomers themselves. The molecular mechanics method used allowed the start of the polymerization of UF resins on the surfaces of cellulose be followed. This was achieved
|
Figure 3 Averages, minima, and averages per atom of the interaction energy of UF oligomers with crystalline cellulose I (in kcal/mol) (negative signs indicate attractive interactions hence adhesion). (From Refs. 6, 7.) |
by comparing the different energy levels of the different oligomers as the reaction proceeds from one oligomer to the next one (Fig. 3). The experimental consequence of this study was the development of a method to evaluate comparatively the applied performance of UF resin prepared according to different procedures just starting from the relative abundance of the various UF oligomers in each resin and their molecular mechanics calculated energy of interfacial interaction [6,7,45]. Similar results were also obtained with a more comprehensive investigation of the oligomers of PF resins [10].
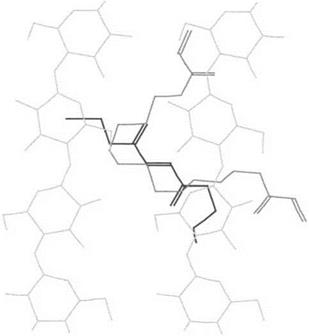
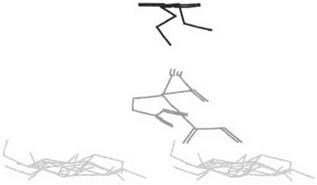
It is however, with the more complex and comprehensive investigation of ternary systems that this molecular mechanics approach started to yield results of greater interest on the fundamental principles of adhesion [32]. Ternary systems present two interfaces because they are composed of three molecular species, namely the cellulose substrate, a photopolymerizable primer resin, and a top coat alkyd/polyester varnish [32]. This work was started mainly to address the concept of flexibility of a surface finish system on lignocellulosic materials but led to some unexpected and rewarding results on adhesion too. Examples of the visualization of the conformations of minimum energy of ternary systems are shown in Figs. 4-6.
Three photopolymerizable primer monomers, namely the linear hexanediol diacrylate (HDDA), the branched trimethylol propane triacrylate (TMPTA), and the linear tripropyleneglycol diacrylate (TPGDA), and a model of a linear unsaturated polyester/ alkyd varnish repeating unit were used for the study. A model of the two top chains of an elementary cellulose I crystallite was used as a substrate, the refined conformation of which had already been reported [12].
The number of degrees of freedom for such calculations is considerable and particular techniques, already used in previous work [7-10], were used to facilitate the computation. At the end the total varnish/primer/cellulose assembly was allowed to adjust and minimize the energy of its configuration.
|
Figure 4 Example of planar projection of the minimal energy configuration of a ternary system composed of a cellulose I schematic elementary crystallite surface, the photopolymerizable acrylic primer tripropyleneglycol diacrylate (TPGDA), and a polyester finish. (From Refs. 72, 73.) |
|
Figure 5 Example of perspective view of the ternary system in Fig. 4. (From Refs. 72, 72.) |
|
Figure 6 Example of view along the cellulose crystallite axis of a ternary system similar to that in Fig. 4 but using a different photopolymerizable acrylic primer, namely trimethylolpropane triacrylate (TMPTA). (From Ref. 73.) |
The applied part of this study relied on a standard peel test in which closely set vertical and horizontal cut lines had been incised on the specimen surface, and on a dynamic thermomechanical analysis of finish flexibility at constant temperature [32,33,46].
An equation correlating TMA deflection and interaction energy at the interface was found by its study:
where a is the coefficient of branching by reactive sites, equal to both Flory’s coefficient of branching for polycondensates [47] and a similar coefficient based on reactive carbons in each monomer for radical polymerization compounds. E is the interaction energy of the molecule of monomer with the substrate, hence the thermodymanic work of adhesion, calculated by molecular mechanics. f is the relative deflection obtained for the system by thermomechanical analysis (TMA), m is the maximum ideal number of internal degrees of freedom of the monomer once it is bound in the network. When m is measured experimentally by TMA it is the number-average number of internal degrees of freedom of the segments between cross-linking nodes. k is a constant. This equation can be used to determine the energy of interfacial interaction starting from a measure of TMA deflection, or vice versa. It is then a useful experimental tool.
The results and effectiveness of Eqs. (7) were checked also for other, quite different polymers, namely the polycondensates of resorcinol-formaldehyde, of melamine-urea — formaldehyde (MUF), of PF, and of quebracho and pine polyflavonoid tannins hardened with formaldehyde. The comparison of the energies of interaction obtained by measures of TMA deflection and the use of this formula compared well with the results already obtained for their energy of adhesion with crystalline cellulose in previous work [16-10]. It appears, then, that the formula works also for entanglement rather than just cross — linked networks.
It was also interesting to relate what was discussed above to existing models relating adhesion strength and adhesion energy. In the rheological model [48-53] the peel adhesion strength G is simply equal to the product of the adhesion energy E and a loss function Ф which corresponds to the energy irreversibly dissipated in viscoelastic or plastic deformations in the bulk materials and at the crack tip and which depends on both peel rate v and temperature T. Thus
G = EФ^, T) (8)
The value of Ф is usually far higher than that of E and the energy dissipated can then be considered as the major contribution to the adhesion strength G. It is more convenient in the above equation to use the intrinsic fracture energy G0 of the interface in place of E to have G = G^(v, T). When viscoelastic losses are negligible, Ф tends to one and G must tend towards E. However, the resulting threshold value G0 is generally a few orders of magnitude higher than E. Carre and Schultz [54] have concluded that the value of G0 can be related to E for cross-linked elastomer/substrate assemblies through the expression
Go = Eg(Mc) (9) where g is a function of molecular weight Mc between cross-linked nodes and corresponds to molecular dissipation.
This lead to a few interesting considerations as regards the results obtained by molecular mechanics on the primer/cellulose interfaces. From the equation obtained to relate the flexibility at the interface to the interaction energy it is evident that E ~ m/(af) (the negative sign of E obtained by molecular mechanics is a convention to indicate attraction rather than repulsion). The concept of Mc is intrinsic in the (m/n)/a ratio relating the number of degrees of freedom m per number of atoms n of the segments
between cross-linking nodes as determined by a. This means that g(Mc) can be represented by m(af) and hence
G0 — Em/(af) thus G0 — E2 (10)
This is an important aspect and would at least partly explain in a manner somewhat different from the more accepted explanations why G0 is generally 100 to 1000 times higher than the thermodynamic work of adhesion [48]. It indicates that G — ЕФ(г, T) m(af), or differently expressed G — E2Ф(г, T). Apart from this the interesting consideration still holds that the flexibility at the interface is inversely proportional to both the intrinsic fracture energy and to the peel adhesion strength at least where the effect of Ф is minimized.
This work also defined that the relation of G0 to the thermodynamic work of adhesion WA in tests varied according to the case considered. Thus, the molecular mechanics study showed in general G0 — WA in tests in which viscoelastic dissipation of energy was eliminated or at least strongly minimized. This partly explains why G0 is generally 100 to 1000 times higher than the thermodynamic work of adhesion [48]. This is not all, because it was shown that G0 still included a component based on the viscoelastic properties of the material which it might not be possible to separate from G0, then indeed G0 > WA. However, if the viscoelastic component is all transferred as it should be into the viscoelastic energy dispersion function Ф(г, T), then G0 = WA. It must be noted that it might not be possible to really separate completely the viscoelastic dispersion of energy component from G0 as it is intrinsic to it. Conversely, it was also shown that the theoretical case in which the viscoelastic component characteristic of the material (not the effect of crack tip propagation within the material) had been minimized or eliminated the expression G0 — WA really meant that WA < G0 ^ WA rendering acceptable also the alternative findings by other authors that under certain circumstances G0 — WA.
All the above, and the fact that by definition the molecular mechanics interaction energy is proportional to the thermodynamic work of adhesion, hence kEtot = WA, also brings the interesting consideration that
kEtot < G0 < kEtot where Etot = k[EvdW Ф EH—bond T Eele T Etor] (11)
where the molecular mass Mc of Eq. (9) is represented by the combination of a number of parameters involved in Eq. (11). Mc is represented by the molecular degrees of freedom; the type of atoms involved; the coefficient of molecular branching/cross-linking; the atoms polarizability; the angle and direction of the interactions; the electrostatic charges; the number of effective electrons participating; and the dipolar momenta. The mass is then a parameter used, incorrectly, only as a simplified blanket parameter covering all this. Furthermore, to be conceptually correct even symmetrical and asymmetrical bond/ angles stretching movements, and molecular translational movements, even if their contribution is quite small, should be considered.
All the calculations which have reported up to now were carried out by maintaining unaltered the structure of the elementary cellulose I crystallite in its conformation of minimum energy derived from x-ray diffraction data [55-60] refined and minimized in its atomic coordinates and charges [12,61-65]. The blocking of the cellulose crystallite surface in a fixed, predetermined conformation of minimum energy is a very acceptable assumption given the energetic stability of the crystallite itself. However, it is also of interest to investigate what influence the application of a primer or of a finish can have on the surface conformation of a cellulose crystallite as predicted by a molecular mechanics method. As the calculations involved are considerable, a simpler algorithm was used [66] for the calculations. Thus, the conformation variation of a system composed of the primer and of the finish superimposed on two parallel chains of the elementary crystallite of cellulose I was followed. All the component molecules were allowed to move. At the start the two cellulose chains were in their configurations of minimum energy already calculated. The results obtained were of two types:
(i) the stabilization obtained in terms of total energy of the system indicated that the longer was the segment which relied on secondary forces of adhesion to the cellulose surface the better was the stablization of the system by secondary forces: logically this result should have been expected
(ii) the conformation of the two chains of the cellulose changed, but what was unexpected was that it changed to the conformation of the crystallite of cellulose II [61], i. e. a different, more stable crystalline morphology!
This latter is an interesting result which infers that treatment of a lignocellulosic surface with a surface finish or other polymers might well alter irreversibly the conformation of the structure of some of the wood constituents. It implies that to discuss adhesion in terms of modification of the conformation of only the applied polymer without taking into account the variations induced in the substrate itself by the applied polymer might give only a very partial view of the process of adhesion at the molecular level. Previous, generalized but still very acceptable models [22] in which the substrate is taken as a homogeneous surface of hard or soft spheres can describe very well the cases in which the substrate is constrained in such a way that it cannot modify its configuration. However, these models cannot explain well the cases in which the substrate molecule changes its configuration as a consequence of the interactions exercised on it by another polymer species, at the interface: a far reaching conclusion. Notwithstanding this, the situation for crystalline cellulose I was found to be only partially one of these cases, due to the special limits and constraints to which such a rigid structure is subjected in its natural state.
It is also evident from the above that in the case of the primer substrate systems in which the primer is highly cross-linked and the cellulose crystallite is a highly crystalline solid no diffusion mechanisms at the molecular interface are likely. The situation might well be different when one deals with a molecular interface were reorganization of the substrate as a consequence of the interfacial interaction forces induced by the finish is indeed possible (see above). This is the case of a primer monomer, or even a primer of a low degree of polymerization or cross-linking, on amorphous cellulose or even on a sub elementary cellulose crystallites area. In this case the reported inverse dependence of the peel energy G of the system on, among others, the inverse of the molecular mass (1/M)2/3 applies [48,l67]. It appears again to be confirmed by the dependence on m and a, two parameters clearly linked to the molecular mass of the finish monomer, of the surface finish and of the segments between cross-linking nodes of the network when this exists. That m, n, and a are the key parameters representing the molecular mass is confirmed by the known dependence of peel strength on a 2/3 exponent of the molecular mass [48,67]. This clearly points out the constraints of rotational degrees of freedom (and rotational energy barriers) found for monomers the end atoms of which are constrained [32]. Furthermore, the apparent proportionality of the diffusion coefficient of the movement of reptation to M~2 [48,68-70] appears to be confirmed by the direct proportionality of the interfacial flexibility to the number of degrees of freedom m of the system. The more flexible is the system, hence the greater is the number of its degrees of freedom per unit mass (or per atom) the easier is interdiffusion. This shows again that it is not the molecular mass of the chemical species as such which will determine either the coefficient of diffusion or the relaxation time of reptation, but these two latter undoubted relation to the flexibility of the system which depends on the parameters m, n, a, and E, and especially the per atom values m/n and E/n.
 29 июня, 2015
29 июня, 2015  Malyar
Malyar 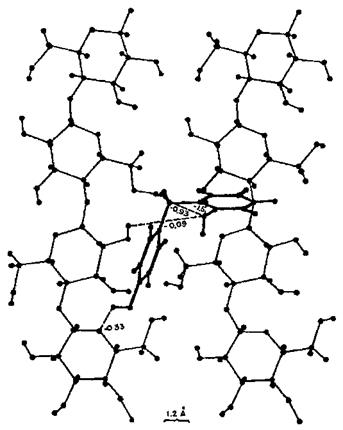

 Опубликовано в рубрике
Опубликовано в рубрике 