В предыдущих главах рассматривались свойства, по существу, идеальных монокристаллических нематиков. Однако ориентации директора, создаваемые подложками в тонких слоях жидкого кристалла, могут быть непараллельными, что вызовет постепенное изменение (искривление) ориентации директора при переходе от одной поверхности к другой. Подобное искажение однородной ориентации директора может иметь место в результате ориентирующего действия внешнего магнитного (или электрического) поля, если его направление не совпадает с ориентацией, которая задается поверхностями подложки. Такие изменения ориентации директора происходят на макроскопических расстояниях (как правило, они составляют несколько микрон) и легко регистрируются оптическими методами. Вместе с тем изменения параметра порядка S в объеме, занимаемом образцом, затухают довольно быстро — обычно на расстоянии, равном нескольким размерам молекул. Таким образом, если пространственные изменения ориентации директора п на расстояниях порядка размера молекулы малы, то такой нематик по-прежнему можно считать локально-одноосным, причем его параметр порядка S(T) имеет постоянное по кристаллу значение, а ориентация директора п(г) меняется. Полное описание порядка в жидком кристалле может быть получено с помощью тензора параметра порядка Q с компонентами
|
J_ 3 |
|
(Г) [п. (г) и3( г) |
8A3j, а, р z, (6.1)
Где 6ар — символ Кронекера, равный 1 для а = Р и нулю во всех остальных случаях. Для однородного образца с директором п, направленным вдоль оси г, отличны от нуля только диагональные компоненты тензора Q:
Q22=± S, Qxx = ~Y S•
Искажение однородной ориентации директора в жидком кристалле можно описать на основе континуальной теории, аналогичной классической теории упругости твердого тела. Согласно теории упругости, при однородной деформации твердого тела в нем возникают силы, препятствующие изменению расстояния между соседними точками тела и стремящиеся возвратить тело
В первоначальное состояние. В нематической жидкости не существует сил, противодействующих изменению расстояния между соседними точками тела, однако возникают возвращающие крутящие моменты, которые препятствуют изменению направления директора. Напряжения, связанные с такими моментами. Франк [54] назвал напряжениями кручения. Он предположил,
|
|
|
|
|
Fox/ К/ |
|
У ‘х |
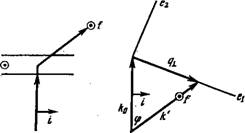
Рис. 6.1. Деформация поперечного изгиба (а), кручения (б) и продольного
Изгиба (в).
Что существует закон, эквивалентный закону ГуКа, согласно которому эти напряжения пропорциональны деформациям искривления, при условии что деформации достаточно малы. Это предположение означает, что плотность свободной энергии является квадратичной функцией деформаций искривления, в которую в качестве коэффициентов входят величины, аналогичные упругим модулям. Дальнейшее рассмотрение проведем в соответствии с работой Франка [54].
Пусть в каждой точке с координатой г одноосного жидкого кристалла направление преимущественной ориентации длинных осей молекул задается директором п(г). Предположим, что ориентация директора, заданная для некоторой точки, медленно меняется с расстоянием и непрерывна в соседних точках. (Знак П, как и прежде, не имеет физического смысла.) В каждой точке с координатой г введем локальную правую декартову систему координат х, у, Z с осью Z вдоль направления п. В этой системе 6 линейных компонент искривления ориентации таковы (рис. 6.1):
S1 = Dnjdx, S2 = дпу! ду (поперечный изгиб),
Tx = —дпу! дху t2 = dnjdy (кручение), (6.2)
Ъх = dnjdz , b2 = dny!dz (продольный изгиб).
Для простоты ограничимся рассмотрением планарной структуры, в которой директор всегда остается перпендикулярным
Некоторой выделенной оси, например оси у. Тогда дпу = 0 и возможными деформациями являются только Sv T2 и Bv Предполагая, что плотность свободной энергии является квадратичной функцией этих деформаций искривления, следует учесть также члены второго порядка [150]:
= д[7]Пх1дх2, Tt = д2пх1ду2, Bb = D2Nx/Dz2,
(6.3)
St = д2пх/дхду, Sb — D2Nx/Dxdz , Tb = D2Nx/Dydz.
Слагаемые, линейные по вторым производным п, имеют тот же порядок величины, что и квадраты первых производных. Разлагая функцию п(г) в ряд Тейлора по степеням х, у, г, имеем
1
Пх (Г) = Atx —F а2у + A3Z+ — (апх2 + а22у2 + A33Z2 + а12ху +
+ A13xz + A23yz) Н — ,
*у (г) = 0,
(6.4)
/£г уг)=[1—пх(т)—пу( г)],/2. В результате получаем следующие соотношения: — й2 = T2, й3 = 61? ап = Ss, а2 2 = Tt, а33 = Bb, а12 = St, а13 =— Sb, а23 = Tb.
Поскольку п2х + п2у + N2Z = I, первые производные пх исчезают, а члены более высокого порядка можно не рассматривать, так как они могут быть выражены через производные пх и Пу.
Будем считать, что разность плотностей свободной энергии искаженного нематика и нематика в состоянии с однородной ориентацией директора является квадратичной функцией трех компонент деформации искривления, определяемых выражениями (6.2), и линейной функцией членов второго порядка, определяемых выражениями (6.3):
3 3 3
Янных в уравнении (6.5) может быть существенно уменьшено Г54]. Если принять го внимание эквивалентность п и —п, то число независимых постоянных уменьшается. Например, из членов второго порядка отличен от нуля только член, соответствующий комбинации продольного и поперечного изгибов. Ограничиваясь планарной конфигурацией, находим следующее общее выражение для плотности свободной энергии:
^dist — К2 (t, + t2) + kV {d1 +d2)+± kn (*! + S2)2 +
+ A« (h + t2f + ± Кзз ( 6? + bt) , (6.6)
Где члены второго порядка, соответствующие комбинации продольного и поперечного изгибов, обозначены через Di и Di. Соотношение (6.6) можно упростить следующим образом. Поскольку свободная энергия дается выражением
F = f FaMdV, (6.7)
То члены Рида уи, где и(г) —произвольное векторное полет могут быть преобразованы в поверхностные интегралы (согласно теореме Гаусса; см. приложение). Следовательно, при рассмотрении объемных свойств нематического жидкого кристалла подобные члены мсжно опустить. Замечая, чю
(d, + d2) + (sx + s2y — ( Ь? + b22) = у (N • Yn), (6.8)
Применим эти соображения к члену, содержащему к[И введем перенормированные константы с помощью соотношений
К, = кп — 2к® , К3 = к33 + 2kf. (6.9)
Уравнение (6.6) отличается от других известных аналогичных уравнений отсутствием члена (£22 + Дзд^ОД -f TЧто обусловлено исходным ограничением рассмотрения только планарной конфигурации. Это ограничение, однако, не играет сущест — венной. роли, поскольку можно написать
Дпх Дпу дпу "I L1L2 — ~—
Дх д у дх ду
Дх х ду ) ду х дх )
Поэтому член, содержащий множитель к22 + к2А, также дает вклад только в поверхностную энергию. Обозначая К2 = £22, определяя величину T0 соотношением T0 = —к21К2 и вводя в уравнение (6.6) постоянное слагаемое уК2t$, приходим к формуле
Delist = Y К + S2y + К2 (;11 + T2 — t0)* + K3(b2{4- bl)l (6.11)
Очевидно, что величина T0 характеризует искажение ориентации директора в результате деформации кручения в равновесном состоянии. Для нематической фазы свободная энергия должна быть инвариантна при переходе от правой системы координат к левой. Это требование приводит к равенству кч — 0 и, следовательно, дает = О — Для хиральной нематической фазы T0 0.
Уравнение (6.11) можно записать в векторной форме, учитывая, что
Yn = Dnjdx + дпу! ду = Sx + S2 , N • YXn = дпу/дх — Dnjdy = — (Tx + J2), (6.12)
(NXVXn)2 = (N • Yn)2 = (Dnjdz)* + (Dny/Dz)2 = B+B.
Подстановка соотношений (6.12) в уравнение (6.11) приводит при T0 — 0 к основному уравнению континуальной теории упругости для нематиков:
^ы = Y (v • n)« + К, (п • vxn)« + К3 (п • vn)»]. (6.13)
Постоянные К2 и Кг часто называют постоянными Озеена — Франка.
Приведенный здесь вывод отличается от обычного использованием перенормировки, согласно соотношениям (6.9), ,пля К1 и К3 [150]. Хотя такая перенормировка не отражается на окончательном виде уравнения (6.13), она существенна для расчетов Кг и К3 на основе молекулярных моделей. В этом случае рассматривается энергия взаимодействия молекул, имеющих различную преимущественную ориентацию директора, и расчет величины Кг отличается от соответствующего расчета кп. Поскольку эксперимент показывает, что состояние с однородной ориентацией директора устойчиво, все постоянные К1, К2 и К3 Должны быть положительными, что совсем не обязательно для Кц и к33.
Чтобы получить условия равновесия в объеме нематика, нужно найти минимум полной упругой энергии, связанной с искажением ориентации директора. При наличии внешнего магнитного поля в уравнение энергии надо ввести дополнительный член JCm. уравнение (3.8)]
•^Magn — ~~ А/ (В • п)2 (6.14)
(в выражении /nagn опущено постоянное слагаемое, не зависящее от п). В случае электрического поля в то же уравнение войдет дополнительно плотность свободной энергии
(6.15)
Величина Fdist в соответствии с выражением (6.13) является функцией п(г) и градиентов
= "Г- ‘ Р = 2’ 3> <[8]-16)
Где величины ха означают три компоненты радиуса-вектора г Вдоль осей х, г/, Z. Формально условие равновесия может быть выражено таким образом, что полная энергия, получаемая при подстановке уравнений (6.13) — (6.15) в уравнение (6.7), стационарна относительно таких изменений ориентации директора П(г), которые удовлетворяют равенству п2 1. Вспомним, что для нахождения условий стационарности интеграла по отношению к вариации интегрального выражения функция должна удовлетворять уравнению Эйлера —Лагранжа [136]. Мы должны рассмотреть функциональную производную
А. = — Нг — +2-Т—Г1′ «=1.2,3. (6.17)
Дпа р дхР Dg?A
Вектор H, введенный этим соотношением, называют молекулярНым полем. В состоянии равновесия директор в каждой точке жидкого кристалла должен быть параллельным молекулярному полю. Обзор формальной теории равновесия жидких кристаллов дан Эриксеном [51].
Для измерения упругих постоянных нематических жидких кристаллов используются различные методы. Ниже обсуждаются наиболее важные из таких методов.
Методы, основанные на изучении перехода Фредерикса
Термин переход Фредерикса означает деформацию директора в слое жидкого кристалла с однородной ориентацией, вызванную внешним магнитным полем Н.
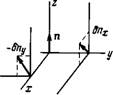
Три практически важных случая схематически показаны на рис. 6.2. В качестве примера рассмотрим случай однородного планарного слоя толщиной D (рис. 6.2, а). Примем в качестве
, 1 ,
Граничного условия, что при Z =±-j« нематик сильно сцеплен с поверхностью. Пусть магнитное поле будет приложено
Вдоль оси Z. При увеличении напряженности поля выше некоторого критического значения Нс (рис. 6.3) возникает посте^ пенное изменение картины ориентации директора. Для полей Н <С Нс равновесное состояние показано на рис. 6.3, а.
|
■//////// |
|
‘////////ZZ/ууууууу |
///////////////////.
|
Н |
Н
Рис. 6.2. Моды поперечного изгиба (а), кручения (б) и продольного изгиба (в) для перехода Фредерикса.
(Направление директора всюду совпадает с осью у.) В этом случае малые флуктуации ориентации директора будут затухать, поскольку стабилизирующий упругий крутящий момент больше, чем дестабилизирующий магнитный крутящий момент. При Н>НС возникает состояние неустойчивого равновесия: даже при незначительной флуктуации система скачком переходит в одно из двух возможных устойчивых состояний, обозначенных буквами б и г на рис. 6.3. На практике система находится в состоянии б в одной области кристалла и в состоянии г в другой его области; переходную область между ними (область
Изменения ориентации директора — инверсную стенку) можно наблюдать при помощи поляризационного микроскопа. Угол наклона 0 директора в средней плоскости слоя относительно плоскости (Х, у) постепенно меняется от нуля до 90° при Н —(рис. 6.3, а, б, в или а, г, д).
|
Н*НС н>нс н»нс
|
|
А б б |
|
Г д Рис. 6.3. Деформация расположения директора выше порога для моды поперечного изгиба. |
Рассмотрим описанный эффект более подробно. При любом заданном поле устойчивое равновесное состояние можно найти, минимизируя полную свободную энергию по отношению к вариациям ориентации директора. Если через 0(z) обозначить угол между директором п и плоскостью (х, т/), то п = [0, cos0(z), sin0(z)]. Полная свободная
Энергия на единицу площади поверхности слоя равна D! 2
F= j* [(^cos^+ /f3sin2e)(^6/dz)2— |x0 Az52sin2 6] Dz. (6.18)
О
Функция 0(z) должна быть такой, чтобы функционал F был минимальным, причем 0—0 для Z =. ±D!2. Это условие приводит к уравнению Эйлера—Лагранжа, которое может быть записано следующим образом:
(Я! Cos2 0 + К3 sin2 0) (DQ/Dz)2 + р-1 А у В2 sin2 0 = С. (6.19)
Постоянную С можно определить, используя то обстоятельство, что при Z 0 0(z) имеет максимальное значение 0т. Следовательно, DQ/Dz = 0, С = po^X^si^Bm — Поэтому уравнение (6.19) можно записать в виде
Bdz = Г Ji. ^ +
I Ах sin2 6m — sin2 0 J 7
Чтобы найти нетривиальные решения, сначала ограничимся малыми значениями 0 и используем приближенные равенства Sin20 » 02 и sin20m « Qm, При расчете критического поля опустим второе слагаемое в выражении (6.20). Тогда
Hdz = (МАу)’2 ( 0^ — 02)~V, d0 . (6.21)
Интегрирование уравнения (6.21) в пределах :от 0 = 0т до 0 = = 0 и от Z = 0 до z = D!2 позволяет получить выражение
Hvd = it (^KJAx)’2 ■ (6.22)
При Н < Нс минимальная энергия получается для Q(Z) = = 0 при всех значениях Z. Полное решение для произвольных полей Ц78] есть
Н1НС = (2/тг) (1 + к sin2 0m)~I/2 П (а2, к), (6.23)
Где
Х = (К3-К1)/К1;
A2 = *sin20m/(l + *sin20m),
K2 = sin2 0m (1 + *)/(l + * sin2 0m)
И П(а2, K) есть полный эллиптический интеграл третьего рода. Как видно из уравнения (6.20), для Н>Н с деформация зависит от отношения KJKV
Для гомеотропного слоя, который находится в поле, параллельном плоскости (х, у (рис. 6.2, в), приведенные выше ре — зулътаты остаются справедливыми, если заменить Кг на К3,
И наоборот, или (иначе) 0 на —0. Для однородного планар-
Ного слоя, который находится в поле, приложенном вдоль оси Х (рис. 6.2, б), ситуация будет несколько иной. В этом случае возникает чистое кручение, а деформация при всех значениях поля зависит только от величины К2. Деформация дается формулой [178]
Н1НС = (2/ic) К (sin2 ф), (6.24)
Где ф —угол кручения, A AT(sin^) —полный эллиптический интеграл первого рода.
В заключение уравнение (6.22) можно обобщить для всех трех случаев, показанных на рис. 6.2, т. е. случаев, соответствующих модам поперечного изгиба, кручения и продольного изгиба:
Ц^ДXH2CD2 = I = 1, 2, 3. (6.25)
Практический интерес представляет также планарный слой, в котором деформация директора кручением создается за счет поворота верхней подложки на некоторый угол ф по отношению к преимущественному направлению нижней подложки (рис. 2.2, в при ф =я/2). Если приложить поле в направлении Z, то вновь возникает нарушение однородной ориентации директора при напряженности поля, превышающей критическое значение [123]:
Р^ДXffcd2 = Кхъ* НЬ (К3 — 2К2) Ф2. (6.26)
При напряженности поля Н Нс оптические свойства такого образца резко меняются, что позволяет применять этот эффект для дисплеев. В этом случае, конечно, вместо магнитного поля нужно использовать электрическое.
Из приведенного обсуждения ясно, что упругие постоянные конкретного нематогенного соединения можно получить, измеряя значения критических полей для трех различных случаев. В принципе для измерения средней степени порядка можно использовать любую анизотропную характеристику, например диэлектрическую проницаемость, электропроводность или теплопроводность. Поскольку зондирующие поля обычно прикладываются перпендикулярно слою, эти методы пригодны только для мод поперечного или продольного изгиба и не пригодны для моды кручения.
Нарушение однородной ориентации директора наиболее точно можно обнаружить оптическими методами. В случае поперечного изгиба прохождение световой волны, поляризованной вдоль оси х, описывается обычным показателем преломления
п0, не зависящим от искажения ориентации директора. Если волна поляризована вдоль оси г/, то показатель преломления равен Пе для Н <С Нс, а в остальных случаях его локальное значение п определяется выражением
П (Z) = пеп0 ( П2е sin2 9 + п0 cos2 e)~v* . (6.27)
|
(6.28) |
|
|
Луч света, поляризованный в произвольном направлении, расщепится на обыкновенный и необыкновенный лучи, которые могут интерферировать в анализаторе. Разность оптических длин пути этих лучей (отнесенная к длине волны) равна
D/2
& = (2A) j [n(z)—n0J dz.
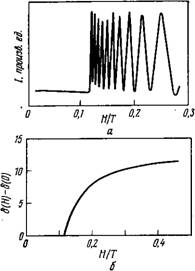
Следовательно, интенсивность прошедшего света обнаруживает ряд минимумов и максимумов, соответствующих целым или полуцелым значениям б, что иллюстрирует рис. 6.4. Аналогичное рассуждение можно провести для моды продольного изгиба. Решение уравнения (6.28) обсуждалось в работах [178]. В случае кручения разность хода нормально падающих лучей отсутствует. Образец можно разделить на две половины, которые дают равный, но противоположный по знаку вклад в величину б. Чтобы появился эффект, необходимо, чтобы падающая световая волна, составляла некоторый угол с нормалью к слою. Самый изящный метод изучения такого эффекта — наблюдение коноскопических фигур. Система характерных для однородного планарного слоя коноскопических фигур — семейство гипербол с общей осью, параллельной директору,— начинает поворачиваться, когда!?>Нс.
При экспериментальном изучении переходов Фредерикса встречаются различные осложнения. Некоторые из них кратко рассматриваются ниже.
1. Из уравнения (6.26) вид — Рис G 4
НО, ЧТО величина Н с обратно в _ осцилляцпи интенсивности прошедшего
Пропорциональна толщине D света при переходе Фредерикса выше поро-
/ га (мода поперечного изгиба); б — разность СЛОЯ нематика (впервые ЭТО на- фаз для той же конфигурации.
Блюдал Фредерике). При выводе этой зависимости предполагалось, что на поверхностях жидкого кристалла имеет место сильное сцепление вещества с подложкой. Если это предположение нарушается, деформация ориентации директора будет соответствовать эффективной толщине образца D + Ъ (а не D), и поэтому значения Н с понизятся. Экстраполированная длина b является мерой поверхностной энергии, и ее можно определять по данным измерений при различных толщинах слоя. Экспериментально установлено, что при различной обработке поверхности действительно получаются различные значения Нс [93].
2. До сих пор рассматривалось теоретическое описание случая. когда Н п. Если это условие не выполнено, критическое поле фактически отсутствует. Теоретическое описание перехода Фредерикса в случае полей, не перпендикулярных направлению директора, приведено в обзоре [35]. Оказалось, что при малых (~1°) углах между Н и нормалью к п уже происходит размытие зависимости 8 от Я вблизи Нс (рис. 6.4, б). Это затрудняет экстраполяцию, необходимую для нахождения величины Н и приводит к заниженным значениям Н с.
3. Если слой жидкого кристалла помещается в электрическое поле, то деформация ориентации директора во многих отношениях аналогична описанной выше [67]. Однако в этом случае возникают осложнения из-за трех эффектов. Во-первых, из-за анизотропии проводимости: при нарушении однородной ориентации директора может возникнуть пространственный заряд, который окажет влияние на переход [66]. Во-вторых, даже если нематик не является проводником, возмущение ориентации директора может создать электрическую поляризацию. Этот эффект, названный флексоэлектричеством (он является аналогом пьезоэлектричества в твердых телах), зависит от искривления ориентации директора (см., например, [35]). Наконец, при напряженности выше критической электрическое поле в слое становится неоднородным.
Вообще говоря, обе величины, как К1ч так и К3, можно определить при помощи эксперимента. Например, Кг можно найти из величины критического поля, а отношение К3/Кг —из сопоставления экспериментальной и теоретической кривых зависимости б от Н. При этом нужно очень точно знать значения показателей преломления, поскольку этот метод весьма чувствителен к величине Аг. Наличие отмеченных выше трудностей заставляет сомневаться в результатах, полученных таким образом, и поэтому обычно требуется их дополнительная проверка. Во всяком случае, все рассмотренные эффекты показывают, что высокие значения упругих констант (соответствующие высоким критическим полям) более правдоподобны, чем низкие.
Метод, основанный на измерении рассеяния света
Молекулы жидкого кристалла стремятся ориентироваться длинной осью параллельно преимущественному направлению директора, флуктуация относительно которого определяется величиной параметра порядка S. В разных точках пространства ориентация директора п может отличаться от равновесной ориентации п0 на величину
Ьп = п—п0. (6.29)
Малые флуктуации 8п должны быть перпендикулярны п0, поскольку обязательно должно выполняться равенство n2 = 1. Эти флуктуации можно описать в рамках теории упругости, связанной с искривлением. Поэтому такие флуктуации зависят от упругих постоянных. Поскольку на поворот директора как целого не требуется затраты энергии, то энергия, необходимая для создания ориентационных флуктуаций л, мала при большой длине волны флуктуации Я. Так как поляризуемость среды анизотропна, такие флуктуации приведут к флуктуациям оптической диэлектрической проницаемости и, следовательно, к рассеянию света. Вводя волновой вектор Q с помощью выражения Q — 2яп/Х, Где п —средний показатель преломления, видим, что рассеяние при малых Q будет велико, что вызовет помутнение нематика. При I эти длинноволновые моды исчезают и остаются
Только флуктуации проницаемости, связанные с флуктуациями плотности. Поскольку последние энергетически гораздо менее выгодны, жидкость останется прозрачной.
Чтобы более подробно обсудить флуктуации п, рассмотрим образец нематика с директором п0, параллельным оси Z. Флуктуации в любой точке координат г можно описать функциями пх(г) и пу(г). Полная упругая энергия, связанная с искривлением ориентации, равна
Как и в теориях, в которых рассматривается движение атомов в твердых телах, удобно выразить функции пх(г) и пу(г) через компоненты Фурье:
(г) = 2 N* fa) ехР № ‘ г) • (6-3J)
Аналогичное выражение может быть получено и для пу{Г). Обратное преобразование уравнения (6.31) имеет вид
Пх (q) = V’1 j пх (г) exp (— iq. г) DV , (6.32)
Где V — объем образца. Поэтому
{Dnjdxf = 2 I и* (Q) I2 Ql и т. д. (6.33)
Q
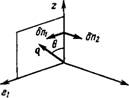
Для каждого волнового" вектора Q можно повернуть систему координат х, г/, Z вокруг оси Z таким образом, чтобы новая ось Х’ совпала с единичным вектором ех, который перпендикулярен оси Z в плоскости (q, z) (рис. 6.5). Тогда ось у’ совпадет с вектором е2. В этой новой системе координат qy = 0, и компонентами n(q) вдоль е* будут па (q) (а =.-=1,2). Используя уравнения (6.31). можно записать свободную энергию в простой форме:
F = 2 11 (я)12(^ + +
Q
+ | n2(q)2(K2ql+K3q)]9 (6.34)
Где G и = Qz = Q cosB и QL = Q sin0 (рис. 6.5). Чтобы вычислить среднее значение (|na(q)2|) величины |rca(q)|2, можно использовать закон равнораспределения.
|
|
|
Рис. 6.5. Определение собственных Bi мод для длинноволновых флуктуа — цпй. |
Для классической системы, находящейся в тепловом равновесии, средняя энергия, приходящаяся на одну степень свободы,
Равна — кв Т. Поэтому получаем
< I Na (Q) |«> = ( kBT/V) (Ка q + Ktq . (6.35)
Уравнение (6.35) является основным уравнением в теории флук — туаций для нематиков [60]. Благодаря использованию закона равнораспределения оказалось возможным получить выражение для тепловых флуктуаций п, которое не зависит от динамических процессов, в действительности управляющих флуктуаци — ями п.
Перейдем теперь к влиянию флуктуаций п на тензор оптической диэлектрической проницаемости. В качестве примера рассмотрим случай, показанный на рис. 6.6. Напряженность электрического поля падающей световой волны можно описать формулой
Eln(r) = iЈ0exp(ik0.r), (6.36)
Где Ео —амплитуда, A i —единичный вектор, перпендикулярный волновому вектору к0 падающей волны и определяющий направление поляризации. В этом электрическом поле образец
|
|
|
Оптическая ось |
|
Рис. 6.6. Геометрия для рассеяния луча, поляризованного перпендикулярно директору. |
Нематика приобретает поляризацию Р(г), связанную с Ein(R) Соотношением (5.1). Наблюдение образца ведется из некоторой удаленной точки с координатами г’ = г + R (R велико по сравнению с размерами образца). Найдем выражение для полного поля рассеянной волны Eout(R‘) с волновым вектором k’||R при наличии поляризации, которая характеризуется единичным вектором F. Соответствующая компонента тензора оптической диэлектрической проницаемости есть
6i/ = F — е — i = е + Де (ntnf — — М ,
(6.37)
Где Nt — N—I и == N—F — компоненты п вдоль двух направлений поляризации. Используя уравнение (6.29), находим часть связанную с флуктуациями:
8Ei/ = Ae[ IN(f.8п)+/„(!• 8п)], (6.38)
Где Jу =n0-i и т. д. Разлагая 6п по собственным модам щ и тг2. определенным выше, имеем
8n (q) = е^ (q) + e2n2 (q), (6.39)
И тогда
K|/ = Ae 2 МЯ) (*<*/,;+ *„/аЬ «=1.2, (6.40)
А=1, 2
Где Ia = Iea — компонента I вдоль Ea.
Теперь видно, что флуктуации ориентации директора (изменяющие тензор оптической диэлектрической проницаемости) при наличии электрического поля падающей волны дают флуктуирующую поляризацию Р(г). Согласно классической электромагнитной теории, электрическое поле, которое излучается в направлении R — г’ — г диполем Р(г), колеблющимся с угловой частотой а), равно
Е (г + R) = [со2/(4тге0с2/?)] Pv (г) exp (IkR), (6.41)
Где Pv (г) — компонента Р(г), перпендикулярная R. Для простоты предположим, что анизотропия оптической диэлектрической проницаемости мала и к = ио)/с, где п — средний показатель преломления, а с — скорость света в вакууме. Поле рассеянного света Eout(r’) определяется суммарным эффектом от всех элементов объема образца. Для больших R множитель 1 /R Можно вынести из-под интеграла. Записывая KR — K‘-R = к’-(г’ —г), где к’ —волновой вектор рассеянного света, находим с помсщыо уравнений (5.1) и (6.36)
F • Eout (г’) — (Tb2/4 тсс2) (EJR) Exp (ik’ • г’) Х-
X (Г) exp (— Iq — Г) DV = A (EJR) exp (Ik‘ . Г‘), (6.42)
Где Q = K‘ — K0 и A —амплитуда рассеяния. Интеграл с точностью до множителя V равен компоненте Фурье бегу(г), которая может быть записана как Se^(q) и определяется формулой (6:40). Дифференциальное поперечное сечение рассеяния на единицу телесного угла рассеянного света (вблизи направления к’) равно
Х 2 < I »«(Ч)1*> (‘«/, + «,/»)•. (6.43)
Где угловые скобки означают статистическое усреднение, связанное с тепловыми флуктуациями согласно уравнению (6.35).
Из вида поляризационного множителя в уравнении (6.43) следует, что интенсивность рассеянного света должна иметь максимум при скрещенных николях, в противоположность ситуации для изотропной жидкости. Рассмотрим случай, схематически показанный на рис. 6.6. Как падающий, тай и рассеянный лучи перпендикулярны оси Z. Йадающий луч линейно поляризован в плоскости рассеяния, а рассеянный луч поляризован вдоль
Оси ъщ совпадающей с оптической осью нематика. Обозначая угол рассеяния через ф, имеем
I
— Q± « Arsin (ф/2), ql{ = 0,
= Cos (ф/2), . I2 = sin (ф/2), IB = /i=/2 = 0, /, , = 1. Подставляя эти выражения в уравнение (6.43), получаем
|
Аг2а>4 |
|
Cos2 (у/2) Sin2 (у/2) |
|
Da DQ |
|
Кт |
|
16те2с* В |
|
Kiq |
Ctg2 (ф/2) + KJK2. (6.44)
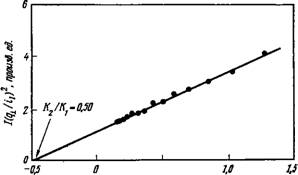
Экспериментально установлено, что соотношение (6.44) действительно приближенно выполняется. Поэтому с помошью линейной экстраполяции можно в принципе находить отношение Кг/К2. При таком определении упругих постоянных следует вносить поправки на двулучепреломление образца нематика. Чтобы с учетом двулучепреломления можно было осуществить линейную экстраполяцию, уравнение (6.44) нужно слегка модифицировать (см., например, 146]). Соответствующий результат показан на рис. 6.7. Аналогичным образом можно получить отношение К31К2 на основе зависимости поперечного сечения рассеяния от угла между Q и оптической осью.
В сильном магнитном поле флуктуации (|raa(q)|2) уменьшаются и становятся обратно пропорциональными величине Ка Q + K3Q +ро* АУВ2, (см- уравнение (6.35)). Если вели-
|
0.5 ‘ Рис. 6.7. Величина отношения K2/Ki, найденная на основе зависимости интенсивности рассеянного света от угла рассеяния (гс-метокси-гс-л-бутил — азоксибензола при 47,5° С, с любезного разрешения Д. К. ван Эка). |
|
W |
Чина Д% известна, то оказывается возможным найти значения всех трех упругих постоянных из измерений относительной интенсивности рассеянного света для различных волновых векторов.
Другие методы определения упругих постоянных
Рассмотрим переход холестерин — нематик. Если магнитное поле напряженностью Н приложить перпендикулярно винтовой оси хирального нематика, то шаг винта увеличивается при условии, что Дх положительно. Соответствующее критическое поле определяется формулой
х~-,Нс = -±- «ад»- (6-45)
При Н>НС жидкий кристалл приобретает нематический порядок. По мере приближения к Н = Нс шаг винта увеличивается по логарифмическому закону. Измерение величины Нс дает информацию относительно /С2, если известны шаг винта и разность Д^. Уравнение (6.45) использовалось практически для определения постоянной К2 хиральных нематиков с большим шагом, которые были получены путем добавления к нематику энантиомор^ных молекул (см., например, [43]). Недостаток этого метода состоит в том, что его нельзя применять для определения значения К2 чистого нематика.
Название нематик связано с нитями, которые можно наблюдать в жидкости под микроскопом. Эти нити представляют собой линии особенностей поля директора жидкого кристалла и называются дисклинациями. Если обойти по контуру вокруг одной из таких линий, директор повернется на целое число тт. Истинную конфигурацию поля директора вблизи дисклинации можно рассчитать с помощью континуальной теории упругости. Для некоторых типов дисклинации конфигурация существенно различна для случаев KJKZ > 1 и K±/K3<Z 1 [54]. Этот факт создает возможность получать информацию о величине отношения КХ1К3, однако такая возможность, по-видимому, еще не была реализована. Прекрасный обзор дефектов и текстур жидких кристаллов дан в гл. 4 книги де Жена [61].
Наконец, для исследования упругих постоянных можно использовать инверсные стенки. Если поле приложено перпендикулярно однородному слою нематика, искажение ориентации директора при Н>НС можно получить двумя способами, соответствующими величине угла между полем и директором 6 и —9 (рис. 6.3). Два соседних домена с отличающейся таким образом ориентацией директора разделены стенкой, внутри которой директор непрерывно меняет ориентацию от +0 до —6- Если поле резко увеличить до значения, превышающего HCJ то часто образуются замкнутые домены. Равновесная форма стенки, окружающей замкнутый домен, представляет собой эллипс. Для случаев поперечного и продольного изгибов отношение осей эллипса равно (К3/К2)}/2 и (К11К2)1^ соответственно 119]. Замкнутая стенка спонтанно сжимается, но, пока размер кольца намного больше его толщины, оно сохраняет форму эллипса с постоянным отношением осей. Таким способом можно определить отношение двух упругих постоянных [122].
|
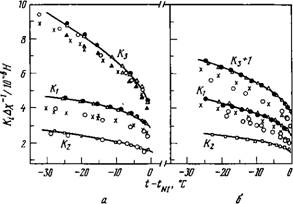
Рис. 6.8. Упругие постоянные ПАА (а) и МББА (б). Различные символы соответствуют различным источникам и различным способам обработки поверхности подложки [93]. |
Перейдем теперь к обсуждению некоторых характерных результатов измерения упругих постоянных. Наиболее подробные измерения были проведены при исследовании переходов Фредерикса, однако большая часть ранее полученных таким образом результатов не слишком достоверна, поскольку существенная роль условий сцепления была понята не полностью. Это иллюстрируется данными, приведенными на рис. 6.8, которые показывают, что различные способы обработки поверхности подложки приводят к различным значениям критического поля и, следовательно, упругих постоянных. Один из классических методов получения гомеотропного порядка состоит в промывке хромовой кислотой. В случае ПАА результаты измерения К3/% в трех разных исследованиях, в каждом из которых использовался этот метод подготовки подложек, практически совпадают. Однако при других методах обработки поверхности были получены более высокие значения. Если независимая информация об условиях сцепления отсутствует, можно только сказать, что наиболее вероятными являются наивысшие значения для Кг И К3. По-видимому, гораздо легче получить, сильное сцепление для моды кручения. В этом случае наличие сильного сцепления можно легко проверить, сопоставляя теорию с экспериментальными данными для вращения коноскопических фигур при Н > > Нс [119]. Для мод поперечного и продольного изгибов такая проверка в принципе также возможна, однако она зависит от точности, с которой известно значение Дп, что вносит дополни^ тельную неопределенность. Упругие постоянные имеют порядок величины 10"11 Н. Так как К ~ Via (где U — энергия взаимодействия и а — размер молекулы), такой порядок величины К Можно ожидать при U « 10 кДж-моль"1 (^0,1 эВ) 1,5 нм.
|
Таблица 6.1 Упругие постоянные некоторых нематических жидких кристаллов (1<Г12 Н)
|
|
[93]. 1129J 1 [H9J. 1 1»1J |
Значения упругих постоянных для некоторых соединений приведены в табл. 6.1. При определении постоянных Кг и К3 МББА и ПАА значения К JДх рассчитывались по наивысшим значениям критических полей (6.7). Значения магнитной восприимчивости и плотности, использованные при еычислснии Kt, Были взяты из работы [189]. В случае МББА приведенные в табл. 6.1 результаты можно сравнить с результатами, полученными другими методами. Из экспериментов по рассеянию света [122] получено К3 = (7,2 ± 1)-10"12 Н. Различие значений К3, полученных разными методами, вероятно, обусловлено несколько меньшей величиной (rNi —Т) в. работе [189]. Значение К3/К1 = 1,3 (табл. 6.1) хорошо согласуется со значением 1,38, полученным из измерений отношения осей эллипсов в методе инверсных стенок [122].
Результаты небольшого числа систематических исследований разных соединений дают возможность предположить, что на упругие постоянные сильно влияет геометрический фактор —длина
Рис. 6.9. Упругие постоянные К Для различных соединений с одинаковым отношением длины молекулы к ее ширине.
1-Х: n = no, r: свнпо; 2-х: n = no, r: с7н16; 3-Х: n = n, r: c7hlft.
«-0*0
L и ширина D молекулы. Из рис. 6.9, например, видно что для некоторых соединений, отличающихся концевыми или мостико — выми группами, но имеющих примерно одинаковую длину и ширину, значения Кг, а также К3/К1 мало отличаются друг от друга. На эту особенность обратили внимание Шадт и Мюллер [183], которые обнаружили лишь небольшое различие значений Кх и К3 у большого числа соединений с различными ядрами, но одинаковыми концевыми группами. Приведенные экспериментальные данные удобно подытожить отдельно для относительно жестких молекул и для молекул, содержащих гибкие группы.
1. Жесткие молекулы. Первые три примера в табл. 6.2 показывают, что если длина молекулы увеличивается за счет добавления относительно жестких групп, то отношение К31Кг возрастает. Обратный эффект наблюдается, когда увеличивается ширина молекулы. Добавление о-гидроксигруппы к МББА приводит к увеличению К1ч а К3 при этом остается приблизительно неизменной [120]. Отсюда можно сделать заключение, что
К3!Кг ~ LID . (6.46)
Ниже будет показано, что такое соотношение можно ожидать на основе теоретического анализа.
|
|
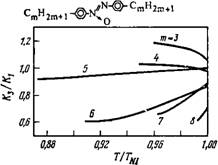
2. Молекулы с гибкими группами. Если к ароматическому ядру молекулы добавляются алкильные цепи или алкоксицепь, то отношение К3/Кх падает (ср. соединение № 4 с №№ 2 и 3 табл. 6.2). Подобный эффект для гомологического ряда соединений показан на рис. 6.10. Падение К3/Кг с ростом длины цепи
Таблица 6.2
Величина отношения KZIK для некоторых соединений с различным отношением длины молекулы к ее ширине1
|
№№ |
Связано с тем обстоятельством, что постоянная Кх увеличивается, а постоянная К3 меняется мало.
Мы располагаем относительно постоянной К2 существенно меньшей информацией, чем для Кг и /С3. До настоящего времени К2 всегда оказывалась наименьшей из трех постоянных. Отношение К21Кг меняется у различных соединений от 0,4 примерно до 0,8, причем К2 При этом остается почти неизменной.
|
Рис. 6.10. Отношение К3/К1 для ряда n-диалкилаз оксибензолов [91]. |
При теоретическом исследовании упругости, связанной с искривлением ориентации директора, часто используется приближение Кх = К2 ~ К3. Приведенные выше экспериментальные данные показывают, что это одноконстантное приближение не соответствует реаль
ной действительности. Вместе с тем имеются соединения, для которых Кг « К3, и если использовать двухконстантное приближение для расчетов, то удается значительно упростить уравнения [см., например, уравнения (6.18)—(6.20)]. Пример такого соединения — /г, тг’-дибутилазоксибензол (ДИБАБ) приведен в табл. 6.1. Для этого соединения отношение К3/Кг Было определено и другим методом — с помощью рассеяния света. Хотя это значение (1,25 ± 0,2) и несколько выше, чем измеренное при исследовании перехода Фредерикса, все же оно довольно хорошо согласуется со значением, приведенным в табл. 6.1.
Прежде чем пытаться интерпретировать эти результаты с помощью молекулярных моделей, необходимо обсудить зависимость упругих постоянных от параметра порядка. В теории Ландау для нематической фазы предполагается, что свободная энергия Т, Qa°) является аналитической функцией тензора параметра порядка Q [уравнение (6.1)]. Полагая, что компоненты тензора малы, можно разложить свободную энергию по степеням Если имеется нарушение однородной ориентации директора, то тензор параметра порядка будет меняться от точки к точке, и в это разложение нужно включить слагаемое с градиентами Qtf. Поэтому с точностью до членов второго порядка по Qap свободную энергию можно записать в виде [61]
|
|
|
+ |
|
(6.47) |
Где ха (а =1,2, 3) означает х, у, Z и Ft —плотность свободной энергии для изотропной фазы. В уравнении (6.47) входят только две упругие постоянные, обозначенные через и Ь2- Чтобы связать Lx и Ь2 с постоянными Озеена —Франка, нужно подставить выражение (6.1) в уравнение (6.47). Предполагая, что вариации обусловлены только вариациями п и что S в объеме жидкого кристалла имеет постоянное значение, можно привести выражение для свободной энергии, связанной с искажением, к виду
^dist = S2 + ± Lij (V • n)2 + Lx (n. vxn)2 +
+ Vn)*J. (6.48)
Сравнение уравнений (6.48) и (6.13) дает
К1 = К3 = 2S2 (L, + L2j, K2 = 2S*LV (6.49)
Следовательно, любая теория, не учитывающая слагаемых более высокого порядка, чем S2, должна предсказывать равенство Кг = К3. Кроме того, эти упругие постоянные должны меняться с температурой пропорционально S2. Часто считают, что такая температурная зависимость имеет место всетда, однако из вышеприведенного разложения Ландау видно, что это неверно. Температурную зависимость Kt ~ S2 можно ожидать только в том случае, когда справедливо двухконстантное приближение.
Из экспериментальных результатов (рис. 6.10) следует, что последнее заключение находится в прекрасном согласии с экспериментом. Если Кгж К3, То отношение К3!Кг почти не зависит от температуры. С ростом температуры S падает, и ошибки, связанные с неучетом членов более высокого порядка, становятся менее существенными. Действительно, температурная зависимость К3/Кг в случае К3/Кг ^ 1 такова, что с увеличением температуры значения Кх и К3 сближаются.
Расчет упругих постоянных на основе молекулярных моделей может быть проведен, если рассмотреть энергию взаимодействия между молекулами нематического жидкого кристалла, находящимися в двух элементарных объемах DV и DV‘, причем направления преимущественной ориентации директора в этих объемах слегка отличаются друг от друга. Согласно работе [150]. можно считать эту энергию взаимодействия равной
FdVdV‘. (6.50)
Предположим, что при фиксированных температуре и давлении функция / зависит от относительного расположения двух рассматриваемых объемов и от направлений п и N‘ = п + бп Директора в объемах DV и DV‘ соответственно. Поместим объем . DV в начало системы координат х, у, Z и направим ось Z вдоль п. Направление п’ = п бп выберем в плоскости (х, Z) и обозначим малый угол п’ с осью Z через а (рис. 6.11). При таком специальном выборе системы координат бп « б пх, 8Nz « Ои б пу == = 0. Из уравнений (6.2) и (6.3) видно, что этот выбор не уменьшает общности рассмотрения, поскольку бПх может соответствовать любому из видов деформации. Так как п и п’ —единичные векторы, для малых а имеем
Ьпх = sin а^а. (6.51)
Теперь предположим, что взаимодействие быстро падает с
расстоянием и что взаимодействием можно пренебречь, если расстояние превышает некоторую максимальную в? личину R. Для любого элементарного объема dV находящегося от начала координат на расстоянии, меньшем или равном R, функцию / можно разложить в ряд по степеням а:
/-/.+(-?-) «■+…. <6.52)
д1 )А=0 2 дх — /а=0
Вместе с тем а можно разложить в ряд по относительным координатам х, у, Z элемента DV‘:
Где Xj(I = 1,2, 3) означает х, у, Z. Подстановка в уравнение (6.52) дает
‘-‘•+20:).=»(Z LoXi+1 2 (1′,Lo(Lox
1=1 1 I, /=IL 1
) ]
VidXj ]xi, *;-=0
1
Плотность энергии можно найти, интегрируя / по объему шара
Радиуса Д с центром в начале координат. Приравняем энергию взаимодействия макроскопической энергии искажения. Задавая в уравнении (6.54) соответствующие значения Xt и Xj, можно легко идентифицировать слагаемые, соответствующие продольному и поперечному изгибам, кручению и одновременному продольно-поперечному изгибу второго порядка. При этом получаем
(6.55)
Км =— X^IV.
2 V д* )*=о 3
Чтобы вычислить упругие постоянные с помощью этих формул, нужно предположить определенный вид функции /, описывающей взаимодействия. Неринг и Заупе [151] использовали для этой цели молекулярно-статистическую теорию Майера и Заупе (гл. 1), в которой дисперсионные силы рассматриваются в диполь-дипольном приближении. Если обозначить наведенные дипальные моменты двух молекул 1 и 2, находящихся на
Расстоянии г друг от друга, через Nij и т2, то энергия их взаимодействия запишется в виде
[3 (til! • г) (ш2 • г)/г« — К. т2)/г3]2 . (6.56)
Преимущественная ориентация молекулы 1 определяется вектором п, а молекулы 2 — вектором п’. В приближении среднего поля, считая окружение молекулы сферически симметричным, получаем выражение для энергии взаимодействия
F = _ (ANS/R3)2 [3 (п • г) (п’ • г)/г® — (п • п’)]2. (6.57)
Здесь А — величина, которая зависит только от свойств молекул, N —число молекул на единицу объема и S —параметр порядка. Вычисляя интеграл (6.55) с помощью (6.57), находим [151]
Кп : *22: к33: k{f =(—7): 11 :17 : (- 6).
Таким образом, теория предсказывает, что некоторые из упругих постоянных отрицательны. Однако если использовать соотношения (6.9), то феноменологические постоянные оказываются положительными, какими они и должны быть,
КгК2:К3 =5:11:5.
Как и следовало ожидать, для взаимодействия, пропорционального S2, имеем К = К3. Кроме того, теория предсказывает, в противоречии с экспериментальными результатами, что К2> > Это следует, вероятно, отнести за счет того обстоятельства, что при таких расчетах не учитывалась форма молекул. Для анизотропных молекул пространственную зависимость межмолекулярного потенциала нельзя отделить от угловой зависимости. Тем не менее отношение К3/К1 было связано полуэмпирическим путем с анизотропией окружения молекулы [169, 65].
Потенциал Майера — Заупе можно рассматривать как первое слагаемое в разложении межмолекулярного потенциала по полиномам Лежандра четного порядка. Приест [170] рассмотрел разложение в общем виде и вычислил упругие постоянные, сохранив в разложении два члена. Оказалось что отношение К^!К3 может быть просто связано с отношением PJP2, где Р2 = S, а Р4 — среднее значение четвертого полинома Лежандра:
Р4= — (35 Cos4 Э—30 cos2 Э +3). (6.58)
8
— 1
Вводя К = —G (Ki + Кг + А’3), получим
К J К = 1 + А — ЗД ‘PjPv KJK = 1 — 2Д — A RpJPt, (6.59)
К3’К = 1 + А + 4ДRPi / Р2.
Величины А и 4′ — постоянные, зависящие от молекулярных свойств. Чтобы рассчитать их, нужно сделать дальнейшие допущения. Представив молекулы в виде сфероцилиндров, взаимодействующих как твердые тела, нахрдим [170, 188]:
Д = (2i?2 — 2)/(7Л2 + 20),
Д’ _ JL (3i?2 — 8)/(7Л2 + 20).
Здесь R = (L —D)ID, где L и D — полная длина и диаметр сферо цилиндра. Очевидно, что для любых разумных отношений длины к диаметру обе величины 4 и А’ положительны. Следовательно, предсказание теории, что К2 меньше, чем К и /С3, является правильным. Для положительных Д’ и PJP2 уравнение (6.59) всегда дает К3> К^
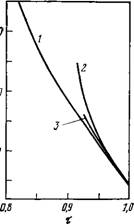
Уравнения (6.59) и (6.60) можно использовать, чтобы рассчитать изменение отношения К3/Кч в зависимости от отношения длины сфероцилиндра к его диаметру. Результаты расчета для различных значений PJP2 показаны на рис. 6.12. Видно, что для положительных значений PJP2 отношение К3/К1 увеличивается с ростом отношения длины к диаметру в хорошем согласии с экспериментальными данными для жестких молекул [117] [ср. с табд. (6.2)].
Приведенные выше результаты указывают, что упругие постоянные молекул с гибкими группами отличаются специфическим поведением в том смысле, что у них имеется дополнительный вклад в упругость, связанный с наличием гибких алкиленовых цепей. Это обстоятельство может быть объяснено следующим образом. Алкильные цепи могут препятствовать скольжению одних молекул вдоль других. Такое движение может оказаться более затрудненным, чем в случае жестких молекул. Это означает, что у ароматических ядер соседних молекул возникает тенденция приблизиться друг к другу. Если образуются кластеры из нескольких молекул, это может привести к появлению эффективной ширины, такой, что L/Deii окажется меньше единицы. Другая возможность состоит в том, что постоянная
К3 становится аномально малой из-за существования бананопо — добных молекулярных конфигураций. Как показано в работе [64], когда молекулы, имеющие бананообразную форму, подвергаются продольному изгибу, деформация может быть частично устранена путем изменения равновесного распределения молекул, повернутых одной стороной «вверх» или «вниз». Подобно тому как собственный дипольный момент вносит вклад в проницаемость, этот эффект может привести на низких частотах к отрицательному вкладу в К3. Во всяком случае, очевидно, что уравнения (6.59) и (6.60) нельзя применять к молекулам с гибкими группами. Поэтому эти уравнения нельзя проверить на МББА, единственном соединении, для которого в настоящее время имеются сведения как о величине РА [86], так и об упругих постоянных.
В заключение можно сказать, что наше понимание молекулярных факторов, которые определяют упругие постоянные нематических жидких кристаллов, довольно ограниченно. Систематически проведенных экспериментов пока мало, но они показывают, что для жестких молекул отношение К3/Кг непосредственно связано с отношением длины молекулы к ее ширине в соответствии с теорией. Если присутствуют гибкие группы, ситуация меняется.
Мы закончим эту главу несколькими замечаниями об упругих свойствах смектических жидких кристаллов. В смектическрй фазе А смектические слои легко изгибаются, что соответствует деформации ориентации директора типа поперечного изгиба. Поэтому Кч, по-видимому, не сильно отличается от соответствующего значения для нематической фазы. Вместе с тем кручение и продольный изгиб практически исключены, поскольку они могут возникать только в том случае, когда меняется толщина смектических слоев. Этот последний эффект похож на сжимаемость жидкости, он требует энергий гораздр больших, чем рассматриваемая нами энергия. Поэтому энергия деформации смек — тической фазы А в низшем порядке (по уп) равна
Fdist = JL V. n)« (6.61)
С*
Это выражение можно обобщить, добавив слагаемое, соответствующее сжимаемости слоев (см., например, [5*]). Выше точки фазового перехода смектик — нематик может возникнуть пред — переходное смектическое упорядочение, особенно если переход близок к переходу второго рода. В этом случае можно ожидать, что К2 и К3 аномально возрастают, если приближаться к переходу со стороны более высоких температур (см., например, [26, 28, 33]). На рис. 6.10 соответствующие части кривых зависимости упругих постоянных от температуры не приведены, чтобы не затемнять «нормальную» температурную зависимость.
 20 января, 2013
20 января, 2013  admin
admin 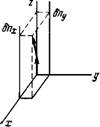


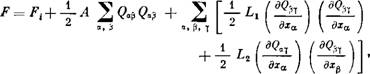
 Опубликовано в рубрике
Опубликовано в рубрике 