Лако-красочные материалы — производство

Нематический жидкий кристалл способен течь так же легко, как и обычная органическая жидкость, молекулы которой по­добны молекулам нематика. Течение жидкого кристалла пред­ставляет собой сложный процесс, так как характеристики тече­ния нематика зависят от угла, который директор составляет с направлениями потока и градиента скорости, а трансляционное движение молекул сопровождается их вращательным движением. Поэтому в большинстве случаев течение возмущает упорядочение и вызывает отклонение директора. Теоретическое рассмотрение взаимосвязи между ориентацией молекул и направлением потока оказывается довольно сложным. В то же время эксперименталь­но направление директора можно измерять и регулировать, например, с помощью внешнего магнитного поля. Определение ориентации директора оптическими методами возможно только в случае тонких образцов жидких кристаллов, поскольку не — матики представляют собой мутную жидкость. Что касается обыч­ных вискозиметрических методов, основанных на использовании капилляров, падающих шаров, вращающихся цилиндров и т. д., то они оказываются практически непригодными. Именно этим объясняется небольшое количество соответствующих экспери­ментальных данных, которые можно было бы интерпретировать количественно.

Для анализа проблемы вязкости жидких кристаллов исполь­зуем следующий подход. Сначала приведем основные уравнения гидродинамики изотропной вязкой жидкости (см., например, [114]) и затем обобщим их на случай простого сдвигового тече­ния нематика (т. е. течения с постоянным градиентом скорости) при ориентации директора, строго регулируемой внешним полем. Далее рассмотрим вопрос, связанный с ориентацией директора при течении нематика в отсутствие внешнего поля, и введем пять независимых коэффициентов, которые имеют размерность вяз­кости и входят в выражение для тензора вязких напряжений. После этого обсудим методы исследований и основные экспери­ментальные данные, показывающие зависимость коэффициентов вязкости от температуры и параметра порядка. Следует под­черкнуть, что мы ограничимся обсуждением только коэффициен­тов вязкости. Обзор интересных неустойчивостей, которые по­являются в гидродинамике нематиков, дан в работе [41].

Явления, рассматриваемые в механике жидкости, являются макроскопическими, поэтому жидкость представляется как не­прерывная среда. При этом предполагается, что в любом малом элементе объема жидкости содержится очень большое количество молекул. Состояние движущейся жидкости характеризуется ее скоростью V(r, T) и любыми двумя термодинамическими вели­чинами, например давлением р(г, T) и плотностью жидкости р(г, T). В случае нематиков необходимо ввести в рассмотрение директор п(г, T). Заметим, что все эти величины относятся к эле­менту объема жидкости, находящемуся в данный момент вре­мени T в данной точке пространства с координатами г == (х, г/, z), а не к фиксированному элементу объема жидкости, который со временем перемещается в пространстве.

Рассмотрим вначале уравнение непрерывности. Масса жид­кости, протекающей за единицу времени через единицу площади поверхности, равна компоненте вектора Pv, перпендикулярной этому элементу поверхности. Полный поток pv через поверхность, ограничивающую единичный объем, равен скорости изменения плотности жидкости в этом объеме:

V.(pv) = -5p/5< или ЈiЈ!>2 (7.1)

Дха Dt

Где через ха (а = 1, 2, 3) обозначены переменные х, г/, Z. Будем использовать такое обозначение всюду в данной главе и записы­вать произведения векторов и тензоров, выражаемые через суммы произведений их компонент (типа а«Ь = ахЪх + ауЪу + + (izbg), в виде произведения аа bat опуская знак суммы. Следо­вательно, если в каком-либо члене уравнения дважды встреча­ются индексы, обозначенные греческими буквами, это означает суммирование по значениям 1, 2, 3. Для удобства приведем не­которые уравнения как в векторной форме, так и для компоненты с индексом а. Ограничимся рассмотрением только несжимаемой жидкости, для которой

Р (г, T) = const, (7.2)

Т. е. исключим из рассмотрения явления типа распространения звуковых волн. В этом приближении из уравнения (7.1) находим

У • V = 0 или (7.3) дха

Перейдем теперь к уравнению движения. Для небольшого объема жидкости имеем

Р dvldt=f, (7.4)

Где / — сила, действующая на единицу объема. Ускорение Dv/Dt Относится к конкретному элементу объема жидкости и не равно ускорению в фиксированной точке пространства. За небольшой промежуток времени Dt жидкость переместится в направлении х На величину Vxdt, а в направлениях у и Z — на Vvdt и Vzdt соот­ветственно. Поэтому если скорость элемента объема жидкости в момент времени T равна v (х, у, Z), то его же скорость в момент времени T + Dt будет (х + Vxdt, у + Vydt, Z + Vzdt, T + Dt). Используя определение частной производной, имеем

V (х + vxdt, У + vydt, z + vzdt, t + dt) = v (.r, y, z, t) +

+ (dv/dx) vxdt + (dv/dy) vydt + (dv/dz) vzdt. (7.5)

Тогда ускорение равно

D/Dt = D/Dt + (v. у) v. (7.6)

В общем случае / может быть представлена как сумма нескольких составляющих. Во-первых, на элемент объема жидкости дейст­вует сила, определяемая градиентом давления (—Vp). Во-вто^ рых, действуют внешние силы, которые можно описать потен­циалом ф (гравитационное, электрическое или магнитное поле). В результате в выражении (7.4) появляется дополнительный член —Уф. (Действие внешних сил мы пока рассматривать не будем.) Наконец, при наличии сил, обусловленных вязкостью, уравне­ние (7.4) принимает вид

Р 1(дЩ + (v — у) v] = — ур + /visc,

Или

Если ввести тензор напряжений а (представляющих собой силу, действующую на единицу площади), то уравнение (7.7) мсжно переписать в виде

Где компоненты тензора напряжений равны

(7-9)

Здесь 6а;з —символ Кронекера, а а^ — компоненты тензора вязких напряжений. Можно предположить, что для малых гра­диентов скорости величина аар является линейной функцией пространственных производных скорости Dv* /дх$ (при v = const тензор оар должен быть равен нулю). Далее, если молекулы жидкости совершают однородное вращательное движение с у г-
ловой скоростью Q0> то V = Й0 X г и dva! дх$ = —dvjd. r0t Оче­видно, в этом случае тензор атакже должен быть равен нулю. Таким образом, можно записать

Л

Где 1] — коэффициент вязкости. Тензор вязких напряжений пропорционален симметричной части тензора градиента ско­рости. Эту часть обычно характеризуют тензором А с компонен­тами

1Г + Т-)

(7.11)

А’Ха — — —

Дхи Top}

(7.12)

Для несжимаемой жидкости след тензора Л равен нулю [урав­нение (7.3)]. Антисимметричная часть тензора градиента скорости выражается тензором W с компонентами

DvFi _ Дха dip J

А связана с вектором со ротора скорости

(7.13)

Ш = — у 2 V

VSS—W😡, IVхХ

Вихре бое течение А =0 Б

Равным локальной угловой скорости жидкости. Разложение тензора градиента скорости на симметричную и антисимметрич­ную части означает, что локально течение может быть представ­лено в виде суперпозиции безвихревого (W = 0) и вихревого (А = 0) течений (рис. 7.1). Подстановка уравнений (7.9) и (7.10)

Сдбигобое течение

БезВихребое течение А

Рис. 7.1. Комбинация безвихревого (а) и вихревого (б) течений, в резуль­тате которой возникает сдвиговое течение (в).

В (7.8) приводит к уравнению Навье — Стокса для несжимаемой изотропной жидкости.

Рассмотрим теперь течение нематического жидкого кристалла при постоянном градиенте скорости (или с постоянной скоростью сдвига). Пусть этот кристалл находится между двумя парал­лельными пластинами, перпендикулярными оси х, скорость те­чения направлена вдоль оси Z, а градиент скорости будет нап­равлен вдоль оси х так, что г;-[0, О, И(х)]. В этом случае эффективная вязкость в соответствии с уравнени­ем (7.10) может быть записана в виде

Axz = rduldx (7.14)

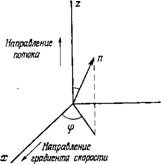
И зависит от ориентации директора П, которая определяется углами ф и 9 (рис. 7.2). Если предположить, что ориентация директора фиксиро­вана с помощью внешнего поля (на­пример, с помощью сильного маг­нитного поля), то возможпы три предельных случая (рис. 7.3, а, б, в):

— Директор параллелен направ­лению градиента скорости (ф = 0, 9 = 90°, г] =

— Директор параллелен направ­лению скорости течения (ф = 0, 9=0, г| = т)2);

— Директор перпендикулярен плоскости сдвига, т. е. плос­кости, в которой лежат векторы градиента скорости и скорости (ф = 90°, 9 = 90°, г] = т|в).

Коэффициенты вязкости т)2 и часто называют коэффи­циентами Месовича. (В оригинальной статье Месовича [146] под коэффициентами т^ и Ri2 понимается вязкость, соответствующая случаям, представленным на рис. 7.3, б и а в отличие от нашего рассмотрения, поскольку мы использовали обозначения Хельф-

Коэффициенты Вязкости Vi % Лз Ш

Коэффициенты кручения — ос2 ос3 — — В градиенте скорости

Рис. 7.2. Схема, показываю­щая ориентацию директора по отношению к плоскости сдви­га. Директор п составляет с осью z угол 6.

Рис. 7,3. Коэффициенты вязкости нематического жидкого кристалла.

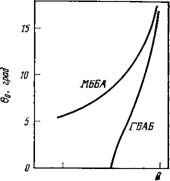
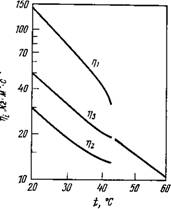
Риха [76, 77].1) Зависимость этих коэффициентов вязкости от температуры для МББА приведена на рис. 7.4. Видно, что в от­личие от зависимостей % и т]2 зависимость т]3 можно рассмат­ривать как продолжение температурной зависимости вязкости изотропной жидкости.

Кроме двух возможных типов потока, изображенных на рис. 7.3, а и б, при которых сдвиговая деформация жидкости

Рис. 1Л. Коэффициенты вязкос­ти Месовича для МББА [57]. Температурная шкала линейна по 1 /Т.

Антисимметрична относительно направлений х и Z, возможно также течение, симметричное от­носительно этих же направлений и соответствующее деформации растяжения (коэффициент вязкос­ти т)12 рис. 7.3, г). Одновременно со сдвиговой деформацией макси­мальный вклад деформации рас­тяжения в течение реализуется, когда директор находится в плос­кости сдвига и составляет угол 45° с направлениями скорости и градиента скорости. В этом случае

45"

Для МББА величина гЛ2 гораздо меньше других коэффициентов вязкости [57], и ее вкладом в тече­ние можно пренебречь. Не ясно, однако, верно ли это в общем случае.

Таким образам, эффективная вязкость нематика при фик­сированном направлении директора (произвольные углы 9 и ср, см. рис. 7.2) равна

RI ^ (ТИ + "12 cos2 6) sin2 0 cos2 ф + Ri2 cos2 9 + Rl3 sin2 9 sin2 <p. (7.16)

До сих пор рассматривалось течение жидкого нематического кристалла, в котором ориентация директора была зафиксирова­на внешним полем. Если снять это ограничение, то в рассмотре­ние необходимо ввести уравнение движения директора. Это урав­нение отражает уникальные свойства нематика и не имеет ана­лога в случае изотропной жидкости. Эксперименты показывают, что чистое вращение директора не обязательно приводит к тече-

О В литературе можно встретить также обозначения г]а, rjj,, гс (т]а = = Л**; гь = Лг; Чс = *}!)•
нию жидкости. Аналогично уравнению (7.6) для производной директора по времени имеем

Dnldt = эп/эT + (v • v)n (7.17)

(N, как и другие характеристики, относится к небольшому эле­менту объема жидкости). Введя локальную угловую скорость директора

Й=пх Dnldt, (7.18)

Получаем уравнение движения директора

IdQ/Dt = rF + Twisc (7.19)

Здесь I —момент инерции, отнесенный к единице объема жид­кости. Левая сторона этого уравнения представляет собой инер — циальный член, а первое слагаемое в правой части — вращаю­щий момент на единицу объема, действующий на директор и обус­ловленный упругими силами (и, возможно, магнитными и элект­рическими полями):

IV =n X Hf (7.20)

Тде H —молекулярное поле [см. уравнение (6.17)]. Второе сла­гаемое в правой части уравнения (7.19) представляет собой вра­щающий момент, действующий на директор и обусловленный вязкостью (силами трения).

Как и прежде, предположим, что это слагаемое является ли­нейной функцией градиента скорости [см. уравнение (7.10)], а также движения директора относительно его окружения. Этот последний эффект определяется не только величиной Dnldt. Если элемент объема жидкости поворачивается как единое целое с угловой скоростью со, вращательный момент, обусловленный вязкостью, будет зависеть от величины

N = (Q — со) х n = Dnldt — со х п. (7.21 а)

Используя выражение (7.13), запишем также

Na (7.21 Ь)

At

Можно ввести две независимые величины, линейные по произ­водным и представляющие собой аксиальные векторы, перпенди­кулярные п [180]:

N X N, n X А • п.

Вращательный момент, обусловленный вязкостью, является сум­мой этих величин, умноженных на соответствующие коэффи-

6-32S Циенты, которые будем называть коэффициентами кручения в градиенте скорости

Rvlsc = — Yin X N — v2n X А • п. (7.22)

При низких частотах инерциальный член уравнения (7.19) гораз­до меньше, чем члены, связанные с упругостью и вязкостью жидкости. Тогда уравнение (7.19) можно рассматривать как ус­ловие равенства вращающих моментов Т? и Rvisc, определяе­мых выражениями (7.20) и (7.22):

N Х h = у±п X N + у2п х А • п. (7.23)

Возвращаясь к случаю течения кристалла при постоянном гра­диенте скорости (рис. 7.2), имеем

V = [0, 0, И (я)], n = (sin 0 cos <р, sin G sin ф, cos 0).

Для этого случая находим

Axz = wxi = — Wzx=’±duldx,

Nz =«угх = — Axznx,

Nx = — соУпг = Axzitz.

Если направление п перпендикулярно плоскости сдвига (0 = = ф = 90°), то вращающий момент отсутствует и Rvisc — 0. Для направления п, лежащего в плоскости сдвига [ф = 0 и п = = (sin0, cos0)], находим момент rvisc, направленный вдоль оси у:

Гу15С = — Ti (nzNx — NxNz) — Y2 (;Nzn^ A]XX — пхщ, A^z) =

=—— (du/dx) iTi + T2 (cos2 0 — sin2 0)]. (7.24)

2

При N, лежащем в плоскости сдвига, момент, вызывающий сдвиг, отсутствует (и директор имеет устойчивую ориентацию) при 0 = = удовлетворяющем условию

Cos 20о = —Т1/Т2 • (7.25)

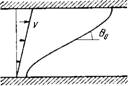
Угол 0о называют углом ориентации директора в потоке. В объ­еме жидкого кристалла, за исключением его тонких поверхност­ных слоев, вращающий упругий момент можно считать равным нулю, и поэтому директор ориентируется так, как показано — на рис. 7.5. Угол ориентации директора в потоке существует, только если LYi/y2|< 1» и не зависит от градиента скорости.

Часто гидродинамические свойства нематического жидкого кристалла описывают более формально. Аналогично уравнению

(7.9) тензор напряжений с учетом ориентации директора можно записать в виде

6F

(7.26)

+ ааЗ ‘

(Та[3 =

Где Ga$ = дпф/дха. По сравнению со случаем изотропной жид­кости в выражении (7.26) имеется дополнительное слагаемое — напряжение, связанное с плотностью F свободной энергии ис­кажения ориентации директора. При небольших деформациях

Рис. 7.5. Схема, показыва­ющая ориентацию директо­ра при сдвиговом течении нематической жидкости.

Это слагаемое мало и обычно им можно пренебречь. Существен­ное различие между нематиком и изотропной жидкостью прояв­ляется в тензоре вязких напряжений аар. Можно ожидать, что его компоненты линейно зависят от А [см. уравнение (7.11)] и N [см. уравнение (7.21)]. Далее, поскольку а'(—п) = а'(п), тензор напряжений должен быть четной функцией п. Наиболее общее выражение тензора для несжимаемого нематика, удовлет­воряющее этим требованиям, есть

% = а4^а,з + п9 Ащ + а2па NЭ + а8юэЛГ« +

+ а5пап>- Arf + (7.27)

Заметим, что этот тензор несимметричен. В выражение (7.27) входят 6 коэффициентов с размерностью вязкости (коэффициенты Лесли). Пароди показал [158], что из соотношений взаимности Онсагера, которые отражают инвариантность микроскопических уравнений движения относительно изменения знака времени, можно получить

Ав =а2+а3 + а6. (7.28)

Поэтому независимыми являются только пять коэффициентов.

В формальной феноменологической теории уравнения (7.27) и (7.28) выводят из рассмотрения диссипации энергии или, как говорят, источника энтропии, связанной со всеми процессами трения в жидкости. Обсуждение этого вопроса можно найти в книге де Жена [61, 124] или в обзоре Лесли [124], где имеются также ссылки и на другие теории. Для нас достаточно отметить
то обстоятельство, что условие роста энтропии накладывает некоторые ограничения на коэффициенты вязкости. Анализируя более подробно уравнение (7.27), видим, что в изотропной фазе отличен от нуля только коэффициент а4. Сравнение с уравне­ниями (7.10) и (7.11) показывает, что

П.. = «4- (7.29)

Вернемся к случаю сдвигового течения жидкого кристалла (рис. 7.2). Тогда для тензора напряжений находим

Oxz = — (Du/Dx) [(2aj cos2 9 — a2 + a5) sin2 9 cos2 <p + 2

+ (A3 + a6)cos29+a4]. (7.30)

Это выражение эквивалентно уравнению (7.16) для эффективной: вязкости, если выполняются соотношения

Л1= Y (—а2 + а4+аб)»

42= у-(а3 + а4 + *бЬ (7.31>

Лз = Y а4» Л12 = <4-

То обстоятельство, что т]1, г]2 и т]3 обязательно положительны,, налагает некоторые ограничения на коэффициенты Лесли. Ис­пользуя соотношения (7.31), уравнение Онсагера —Пароди мож­но записать в виде

42— 4i = «s + a«- (7.32)

Момент, действующий на директор и обусловленный градиен­том скорости, можно выразить через антисимметричную (относи­тельно осей х, г/, Z) часть тензора

(Fvlsc)у =<*’„—<** И Т — Д — (7-33>

Для случая <р = 0 (рис. 7.2) имеем,

Tvisc = (a5 — ae) (njip. — пхп^ АрВ) +

+ («А — АЗ) (nzNx — NxNz) = (du/dx) (аа sin2 9 — a3 cos2 9). (7.34)

Отсюда видно, что коэффициенты —A2 и a3 связывают вращаю­щий момент с градиентом скорости (скоростью сдвига), когда директор параллелен либо градиенту скорости (рис. 7.3, а)г
либо направлению течения (рис. 7.3, б)1. Это дает простую ин­терпретацию соотношения Онсагера — Пароди, записанного в форме (7.32): разности эффективных вязкостей (т]2 и т)^) и коэф­фициентов кручения в градиенте скорости (а3 и — а2) в конфигу­рациях 1 и 2 оказываются равными. Сравнение уравнений (7.34) и (7.24) показывает, что

Yi = а3 — а2, у2 = ссв — а6 . (7.35)

Используя уравнение (7.28), можно получить другое выражение для уг­ла ориентации потока (ср. с урав­нением 7.25):

Tg2 В0 = а3/а2 = (у2 + Ti)/(V2 — Yi) —

(7.36)

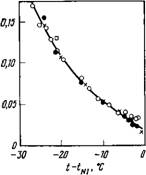
Для нематиков, молекулы которых имеют стержневидную форму, т)1>г]2, условие возрастания энтропии дает а2< 0. Поэтому ориентация потока имеет место только тогда, когда а3< 0. Количественные эксперимен­тальные данные о величине 9 о ДО^ вольно малочисленны (некоторые примеры таких данных приведены на рис. 7.6). Качественные данные показывают, что по крайней мере при Т <С TNi угол 0о часто до­вольно мал (коэффициент |а3| очень мал). Поэтому экспери­менты с потоком, в которых ориентация директора не кон­тролируется внешним полем, как правило, дают величину т2 (директор параллелен направлению скорости потока). Оказы­вается, однако, что в некоторых случаях» а3>0 (эти случаи будут обсуждаться ниже).

Для измерения коэффициентов вязкости нематика можно использовать различные методы. Обсудим наиболее важные из них.

-20 -10

Рис. 7.6. Температурная за­висимость угла ориентации директора при течении нема­тиков [56]. >1

Ц

Методы определения коэффициентов вязкости при сдвиговом течении нематика в магнитном поле

Первые эксперименты по определению коэффициентов вяз­кости при сдвиговом течении нематика в сильном магнитном поле, предназначенном для строгой ориентации директора, были вы-

О В обозначениях Хельфриха —а2 = %2 и аз =
Полнены много лет назад [146, 192]. Недавно они были воспроиз­ведены Гэвиллером [57]. Магнитный момент, действующий на элемент объема, в таких экспериментах должен намного превы­шать вращательный момент, обусловленный градиентом ско­рости. При малом градиенте условие легко выполнить. Устанав­ливая с помощью магнитного паля ту или иную ориентацию директора, можно определить коэффициенты т]2, г3 и т)12. По­этому дополнительное измерение угла 0О оказывается достаточ­ным для нахождения полного набора коэффициентов вязкости.

Первый метод основан на измерении емкости. Если использо­вать прямоугольный капилляр, образованный двумя стеклянными пластинами с проводящими электродами, можно измерять емкость при течении нематика в сильном магнитном поле, параллельном и перпендикулярном скорости потока, а также в отсутствие маг­нитного поля. Когда поток однороден и влиянием пограничных слоев можно пренебречь, результаты измерений позволяют рас­считывать величину 0о [137, 144]. Недостаток этого метода сос­тоит в том, что обычно трудно одновременно с измерением ем­кости проводить оптические наблюдения над потоком, необхо­димые для установления направления ориентации.

Второй метод основан на измерении двулучепреломленйя в нематике в зависимости от скорости его течения [57]. Рассмотрим снова схему, показанную на рис. 7.2. Пусть прямоугольный капилляр образован двумя стеклянными пластинами, положе-

Ние которых определяется координатами х = ±у D. Когда не­матик покоится, директор направлен параллельно оси Z (либо в результате действия соответствующих граничных условий, либо в результате. действия сильного магцитного пшя, параллельного оси Z). Разница оптических длин пути для обыкновенного и не­обыкновенного лучей, падающих перпендикулярно поверхностям стеклянных пластин, равна (Пе — N0)D. При сдвиговом течении эта разность становится равной

D/2

F [п (9) — п0] Dx, —D/2

Где п(9) дается формулой (6.27). Если ориентация директора в потоке установилась, значения 0 меняются с координатой х от нуля до +90 (для х < 0) до —90 (для #>0) соответственно. Изменение разности хода при малых значепиях 0О равно

— Lned(N2E/N20— l)tg*90. (7.37)

Это изменение не зависит от градиента скорости, если толщина переходных слоев вблизи стеклянных пластин и при х = 0 [где
значение функции 0(х) меняется с +0О на —в о! пренебрежимо мала по сравнению с расстоянием между пластинами. Разность хода можно измерять точно, записывая колебания прошедшего света при включении градиента скорости. Таким способом можно определять Tg20o и, следовательно, отношение а3/а2. При нало­жении магнитного поля можно измерять изменение двулуче — прдломления в зависимости от на­пряженности поля и находить отдель­но величину а3/Д% и а2/Д% [57].

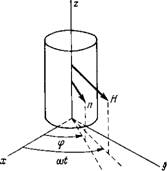
Рис. 7.7. Схема эксперимента, показывающая положение об­Разца нематика по отношению к вращающемуся магнитному нолю Н и осям координат.

Н имеет компоненты (coscp, sincp, 0), так что N=Dn/Dt= (— sincp, coscp, 0)Dy/Dt. Из уравнения (7.22) получаем проекцию на направление Z момента в градиенте скорости RVisc = —У^/Dt. (7.38) В отсутствие эффектов, связанных с упругостью, момент Rvisc, согласно уравнению (7.23), должен уравновешиваться моментом, обусловленным магнитным полем, что дает Yl ^Г " ^ 1 sin 2 И — СР) • (?-39> Решение этого дифференциального уравнения (7.39) зависит от величины О)0 = (рГ1АХ/2т1) Но. (7.40) В случае ш< а)0 система находится в стационарном состоя­нии, при котором сдвиг фаз между полем и директором опреде­ляется формулой Tg (со* — ф) = С00/(1) (a)G/(i)2 —1)^2. (7.41)

Метод вращающегося поля. Рас­смотрим схему, показанную на рис. 7.7. Пусть цилиндрический образец нематика находится в однородном магнитном поле напряженностью Н. Чтобы было достигнуто состояние с минимумом энергии, директор должен ориентироваться параллель­но полю. Если поле медленно вра­щается, то директор следует за ним. но с некоторым отставанием по фазе, величина которого определяется из условия равенства вращающих мо­ментов, связанных с магнитным по­лем и силами трения. Измерение этого сдвига фаз позволяет опреде­лить коэффициент Yi. Как видно из рис. 7.7, вектор напряженности поля Cffocos со*, Но sin а)£, 0), а директор

Для случая о) > ш0 решения приведены в работе [58]. Если предположить, что момент, действующий на нематик, полностью передается на стенки ячейки, то для ш< ш0 он будет равен

Rc0nt=F71o), (7.42)

Где V — объем образца. Величину Rcont можно измерить, под­вешивая образец на кварцевой нити в магнитном поле и измеряя угол поворота при включении поля. Наклон прямой, описы­вающей зависимость отношения rcont/F от со, непосредственно дает величину Yv

В книге де Жена [61] показано, что использование метода вращающего поля связано с принципиальными трудностями вследствие сцепления молекул со стенками ячейки. Из-за нали­чия такого сцепления вращение магнитного поля фактически приводит не к стационарному состоянию, а к относительному кру­чению нематика между параллельными поверхностями ячейки, которое линейно нарастает со временем. Напряжения, вызванные кручением, должны релаксировать путем образования петель дисклинаций. При низких частотах часть объема образца, в ко­торой ориентация директора искажается дисклинациями, по — видимому, мала, чем и объясняется возможность применения этого метода.

Метод, основанный на динамике переходов Фредерикса. Ин­формацию о вязкости нематика можно получить, исследуя его реакцию на внезапное изменение величины приложенного поля. Рассмотрим случай, когда магнитное поле больше критического поля перехода Фредерикса; пусть это поле внезапно выключа­ется. Тогда, если рассмотреть чистое кручение (рис. 6.2), то гидродинамическое течение отсутствует — молекулы поворачи­ваются без какого-либо трансляционного движения, что значи­тельно упрощает анализ. Если приложенное магнитное поле не намного больше критического, то угол кручения ф0(я) мал. По­скольку на границах при Z = обязательно ф =0, то с хорошим приближением имеем

<Po(z) =<Pmcos(7u2/d), (7.43)

Где фт — максимальное искажение ориентации директора при Z =0. Если поле выключить, то моменты, обусловленные вяз­костью и упругостью, равны друг другу [см. уравнение (7.23)], что позволяет написать динамическое уравнение для ф(г, T),

K2d2yldz2 = y±d(f/dt, (7.44)

С начальным условием ф — фо(2) при T = 0.Решение уравнения (7.44) имеет вид

Ф T) = ф0 (Z) exp (— */т), (7.45)

Где время релаксации

Т = угй2/(Ъ2К2) = 10УЛЬХН2С) . (7.46)

Зависимость т от Н~~1 при различных толщинах представляет собой прямую линию, наклон которой определяет величину yJ^X — Заметим, что такое простое рассмотрение не может быть проведено для случая Н р> Н с вследствие допущений, при­нятых при выводе формулы (7.43).

Если вместо кручения имеется поперечный изгиб,, то враще­ние директора приводит к гидродинамическому течению немати­ка: градиент угловой скорости директора п вызывает обратное течение жидкости, в результате чего возникает момент сил тре­ния. Используя условие равенства моментов и уравнение дви­жения, можно получить выражение для т, которое довольно слож­ным образом зависит от отношения Н/Нс. Результат можно записать в виде, подобном уравнению (7.46), однако коэффициент уг при этом заменяется на коэффициент эффективной вязкости У* [163]. На практике значения у* примерно на 10% меньше, чем Yv Особый интерес представляет случай [Н/Н с Тогда коэффициент у* сводится к коэффициенту

Risplay = Vx — а§/г]2. (7.47)

Аналогичная ситуация возникает при продольном изгибе, в пределе Н/Н -^оо получаем

Tlbend=7i1 — «1/%. (7.48)

Поскольку |а3| < |аг|, то при поперечном изгибе поправки к уг обычно малы, но они могут оказаться существенными при деформации гомеотропного образца.

Метод, основанный на изучении рассеяния света. Как уже обсуждалось в предыдущей главе, длинноволновые флуктуации ориентации директора в нематическом жидком кристалле при­водят к сильному рассеянию света. Такие флуктуации [их мож­но представить в виде 6п(г, T) = п(г, T) — п0] возбуждаются в некотором элементе объема и затем релаксируют. Динамику этого процесса можно описать с помбщью гидродинамических урав­нений. Экспериментально зависимость флуктуаций от времени можно наблюдать, изучая модуляцию частоты рассеянного све­та, которая измеряется оптическими методами [45, 154]. Мы не будем подробно обсуждать соответствующие эффекты, а просто подытожим информацию, которую можно получить fc помощью этого метода.

Для данного волнового вектора Q рассеянного света ампли­туда рассеяния определяется двумя независимыми фурье-ком — понентами ^(q) и и2(q) флуктуации бп (рис. 6.5). Напомним, что пг описывает смешанную деформацию, включающую про­дольный и поперечный изгибы, а п2 включает кручение и про­дольный изгиб. Каждую из этих фурье-компонент можно изу­чать отдельно, выбирая соответствующее направление поляри­зации света. Для каждой моды возвращающая сила равна

Ка (q) = Ка Q + Kzq, а = 1, 2 . (7.49)

Далее оказывается, что результаты экспериментальных иссле­дований ширины линии в зависимости от величины волнового вектора можно описать с помощью модели с вязкоупругой ре­лаксацией

•JT "а (Ч) = — Та «а (q) . « = 1, 2 . (7.50)

At

Для спектра интенсивности в соответствии с экспериментальными данными получается единственная лоренцева линия, ширина которой обратно пропорциональна времени релаксации т. Это время определяется выражением

Где коэффициенты эффективной вязкости равны

___________ ( — я а2 )2__________________

9±г12 + Я2± ^ К + аз + «4 + «Б) +

„2 „2 2 ^ ||

Я2±Чз + я

Интерес представляют два случая. Если волновой вектор Q направлен параллельно директору, обе моды оказываются чис-

< eff eff

Тыми модами продольного изгиба, и тогда R]i = т]2 = = T]ben(i Гсм. уравнение (7.48)]. Если вектор q перпендикулярен директору, мода 1 становится чистой модой поперечного изгиба hf = r|splay, см. уравнение (7.47)], а мода 2 — модой чис­того кручения (r]2ff = Yi)- С помощью этого метода устанавли­вается соотношение между упругой постоянной и коэффициентом вязкости. Когда одна из этих величин измерена независимым методом, то можно найти другую величину.

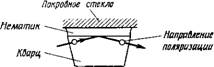
» Метод сдвиговых ультразвуковых волн. Для изучения вяз­кости нематических жидких кристаллов можно использовать
воздействие ультразвука на жидкий кристалл. Классический эксперимент был проведен Мартиноти и Кандо [140], которые измерили коэффициент отражения ультразвуковой сдвиговой волны от границы раздела твердое тело — нематик. Схема экспе­римента показана на рис. 7.8. Коэффициент отражения опреде­ляется формулой

R = (Zs-Zn)/(Zs + Zn), (7.53)

Рис. 7.8. Схема эксперимента, иллюстрирующая отражение сдвиговой ультразвуковой волны от границы раздела твердое тело — нематик.

Где Za и Zn — импедансы твердого тела и нематика соответст­венно. Если величина Zs известна, то измерение коэффициента отражения дает механический импеданс Zn = Rn + IXnJ ко­торый связан с динамической вязкостью соотношением

Л = 2RnXJ ро) = 2Rn /ро), (7.54)

Где аз —частота, р —плотность и в соответствии с эксперимен­том использовано равенство Rn = Хп. В действительности вы­ражение для г] зависит от ориентации директора на границе раз­дела фаз.

Л*

Мы не будем приводить подробных расчетов величины т] для различных случаев, а просто сформулируем основные результаты. Выберем систему координат, такую же, как на рис. 7.2, и будем считать, что УЗ-волны распространяются вдоль оси х, а смещение (скорость) направлено вдоль оси Z. Отличие описываемых экспе­риментов от экспериментов Месовича состоит в том, что для ис­пользуемых в данном случае высоких частот (порядка 50 МГц) глубина проникновения составляет всего лишь несколько ми­крон. Поэтому в направлении распространения УЗ-волн (в на­правлении оси х) появляется большой градиент скорости. Ори­ентация директора на поверхности раздела определяется гранич­ными условиями. Однако в отсутствие ориентирующего магнит­ного поля градиент скорости в ультразвуковой волне создает наклон директора, которым нельзя пренебречь. По этой причине

Коэффициенты т^ и т]2 отличаются от коэффициентов вязкости Ме­совича гг и т)2. Если директор перпендикулярен плоскости сдви­га, то наклон не возникает. В результате получаем

— При п, параллельном градиенту скорости, т^ = г|х + + Y0^1 —Y2/Y‘)’I

— При п параллельном направлению скорости, т]2 = т]2 — — 1-а8(1 + Ya/Ti);

— При п, перпендикулярном плоскости сдвига, т]3 = Ti3.

С помощью уравнений (7.31) и (7.35) легко показать, что У]г =

= т]2 независимо от степени справедливости соотношения Он — сагера — Пароди (7.28).

Эксперименты с применением ультразвука включали также измерение затухания в зависимости от угла между директором и волновым вектором [6]. Изучался также импеданс некоторых смектических жидких кристаллов при наличии сдвиговых волн [106].

Перейдем теперь к обсуждению некоторых типичных значе­ний коэффициентов вязкости. К сожалению, полный набор из­меренных коэффициентов имеется только для очень немногих соединений, например для ПАА (табл. 7.1). Часть приведенных в табл. 7.1 данных была получена Месовичем [146] при изучении сдвигового течения. Авторы работы [91] проанализировали дан­ные Месовича и пришли к выводу, что в его экспериментах маг­нитное поле не было направлено параллельно скорости потока; значения т]2 были получены в предположении 6 о = 0. Вместе с тем оказалось, что если поле параллельно направлению потока, как это было в экспериментах Цветкова и Михайлова [193], то вязкость падает на 16%, что соответствует углу 6 « 9°. Это значение 0О было подтверждено измерениями емкости в магнит-

Таблица 7 Л

Расчетные значенмя

Вязкости ПАА при 122°С (1в~8 кгм-1 с-1)

Экс периментальные значения

^ = 9,2 ±0,4! т]д# = 2,43±0,051 т)3 = 3,4±0,41 = 9°±*1°2

Ч! = 6,8±0,28 Аг = 4 ± 4 А2 = — 6,9±0,2 а« = — 0,2± 0,1 А4 = 6,8 ± 0,8

= 5 ± 1 ав = — 2 =Ь 1

7! = 2,1 ± 0,1 72 = —7,1 ±0,3

Ж

3 [51].

Ном поле и в его отсутствие [137]. Наряду с недавними резуль­татами измерения ^ис учетом соотношения Онсагера — Пароди этих данных достаточно для расчета всех коэффициентов <х1? а2, …, а6.

Рис. 7.9. Температурная зависи­мость коэффициентов вязкости со­единения МББА, связанных с вра­щающим моментом, обусловленным сдвигом.

Как видно из табл. 7.1, точность, с которой определено зна­чение а1? довольно плохая. Ранее считалось, что а^ « 0, и это, как показывают экспериментальные данные, вполне возможно,

Рис. 7.10. Температурная зависи­мость коэффициента вязкости у± МББА, связанного с вращающим моментом, который возникает в ре­зультате использования различных методов исследования.

Метод вращающего магнитного поля: ф — данные работы [58], X— данные рабо­ты [79]; метод динамики перехода Фреде­рикса: □ —данные работы [122]; метод, основанный на изучении рассеяния света: О—данные работы [187]; расчет сделан в соответствии с работой 189].

Если учесть указанную невысокую точность измерения. Ре­зультаты, приведенные в табл. 7.1, удовлетворительно согла­суются с данными, полученными при изучении рассеяния света 1155], однако последние результаты, по-видимому, следует при­знать несколько менее точными.

Для МББА полный набор коэффициентов вязкости был дан Гэвиллером [57], а сдвиговые вязкости более точно были определены Кнеппе и Шнайдером [201]. На основе данных, приведенных на рис. 7.4, и результатов измерений угла 0о можно вычислить коэффициенты а2 и а3 (рис. 7.9). Измерение величины т|45о [уравнение (7.15)] позволяет определить значение п12 так, что набор коэффициентов вязкости оказывается полным. Чтобы проверить данные Гэвиллера, де Же [89] нанёс на один график результаты измерений коэффициента уг, полученные разными авторами с помощью различных методов (рис. 7.10).

По этим данным величина т^ оказалась несколько больше, чем у Гэвиллера. Саммерфорд и др. [190] и Кнеппе и Шнайдер [201} считают, что значение т]1, полученное Гэвиллером, слишком мало, вероятно, из-за неблагоприятного влияния поверхностной ориентации. Коэффициенты вязкости для МББА представлены в табл. 7.2. В качестве первой проверки непротиворечивости экспери­мента и теории используем соотношение Онсагера — Парод и (7.32). Согласно данным табл. 7.2, а4 + а2 = (—110±2) • 10~3 кг • • м^-с"1, т]2 — T|J = (—112±6) • 10"3 кг • м"1 • с"1, так что в преде­лах точности эксперимента соотношение (7.32) удовлетворяется. Второй проверкой может служить сравнение этих результатов с результатами измерений рассеяния света. По данным табл. 7.2 находим

Льепа = Yi — «!/% = 19 X Ю"3 кг — иг1-с"1.

Таблица 7.2 Вязкости МББА при 25°С (Ю-3 кг-м^с"1)1 Экспериментальные зна­чения Расчетные значения Тл = 136 + б2) т)2 = 24,0 ±0,52) 7)з=41,3 ±0,82) Т)12 = -18±62) 0О =5,5 + 0,53) Ti = 108 ± 24) Otj = —18 ± 6 72 = — НО ±2 А2 = — 109 ± 2 А3 = —1,0±0,2 А4 = 83 ± 2 АБ = 80 ± 15 Ав = —34±2 >) *NI — T = 20°С. — 2) [201]. 8) [57]. 4) Данные рис. 7.10.

Экспериментальные результаты для этой величины колеблются между значениями 19 • 10~3 и 21 • 10~3 кг • м"1 • с"1 [71, 189]. Хотя все эти значения не очень точны, поскольку они зависят от правильности выбора значения К3, согласие эксперименталь­ных данных с рассчитанными значениями следует признать ве­ликолепным. Однако необходимо отметить, что значение оказывается не очень чувствительным к изменениям величины у1т До настоящего времени опубликованы подробные данные о вязкости всего лишь нескольких соединений, в том числе ГБАБ [57J и ЦБООА [105]:

ГБАБ ЦБООА

Оба соединения обладают той особенностью, что ниже опреде­ленной температуры величина их коэффициентов вязкости а3 меняет знак и становится положительной. Это означает, что в такой области уравнение (7.36) не имеет действительного решения и установить ориентацию директора в потоке невозможно (рис. 7.6). Первоначально этот результат для ГБАБ был под­вергнут сомнениям авторами работы [144], однако позднее была доказана его правильность [164, 199]. При а3>0 директор со-, вершает беспорядочное движение, которое зависит от предысто­рии поля скоростей в образце [30].

Хельфрих [76] предложил молекулярную теорию ориентации директора при течении нематических жидких кристаллов, моле­кулы которых имеют стержнеобразную форму и могут рассмат­риваться как эллипсоиды вращения. Легко видеть, что для шара момент сил не может возникнуть, поскольку сила действует на лю­бой элемент поверхности по нормали к нему и всегда проходит через центр шара. Если тело представляет собой эллипсоид, момент сил может возникнуть, поскольку в этом случае силы, обусловленные давлением, вообще говоря, не направлены к центру тяжести эллипсоида. Следовательно, в рассматриваемой модели вращающий момент отсутствует, если длинная ось моле­кулы перпендикулярна плоскости сдвига, так как поперечное сечение молекулы этой плоскостью будет круглым. При расчете моментов сил для других ориентаций были сделаны два сущест­венных упрощающих предположения:

— Все эллипсоиды одинаково и жестко ориентированы (что соответствует значению параметра порядка S = 1);

— Жидкий нематик можно рассматривать как газ, в котором твердые эллипсоиды испытывают только упругое взаимодействие при столкновениях. В реальном нематическом жидком кристалле каждая молекула постоянно испытывает притяжение соседей, в результате которого, в противоречии со вторым предположе­нием, возникающий ближний порядок может привести к появ­лению предпочтительных точек соприкосновения молекул, а также изменить частоты столкновений. Оба этих эффекта меняют значения коэффициентов кручения в градиенте скорости, но не влияют на их отношение. Поэтому самым важным результатом теории, развитой на основе этой модели, является установление соотношения

Сс3/а, = (Ь/а)2, (7.55)

Где а и Ъ — длина большой и малой осей эллипсоида соответст­
венно. В действительности уравнение (7.55) остается справед­ливым и в рамках второй модели, использованной Хельфрихом [77]. В этой модели рассматривается плотная жидкость, в кото­рой молекулы по-прежнему считаются ориентированными строго одинаково в определенном направлении, а взаимодействие моле­кул описывается сглаженным эллипсоидальным парным потен­циалом. Для молекул, подобных молекулам ПАА и МББА, от­ношение а! Ъ порядка 5, что дает а3/а2 « 0,04. Сравнение этого значения с данными, приведенными в табл. 7.1 и 7.2, по­казывает очень хорошее согласие с экспериментом.

Различие в поведении ГБАБ (а3>0) и МББА (а3< 0) при: сдвиговом течении кажется особенно поразительным, если учесть, что молекулы этих двух веществ близки по размерам и подобны по химической структуре. Было сделано предположение [56], что за это различие ответственно дипольное взаимодействие циа — ногрупп в ГБАБ. Как отмечалось в гл. 5, из измерений диэлект­рической проницаемости можно сделать вывод, что при наличии сильно полярных групп значительное количество молекул об­разует ансамбли, в которых дипольные моменты оказываются антипараллельными. В первом приближении можно считатьг что у таких молекул появляются выступы (в отличие от молекул ПАА или МББА, имеющих форму правильного эллипсоида). При сдвиговой деформации такая молекула, по-видимому, ис­пытывает воздействие конечного вращающего момента, даже если она ориентирована параллельно направлению течения. Можно ожидать, что этот эффект особенно велик при низких темпера­турах, когда взаимодействие между молекулами, приводящее к образованию ассоциаций, становится более сильным.

(7.56)

Модель Хельфриха можно использовать для нахождения со­отношения между вращающим моментом и вязкостью при сдвиго­вом течении. Если ближний порядок таков, что эллипсоиды стал­киваются только вершинами, а также точками, расположенными по окружности центрального сечения (по-прежнему предпола­гается, что все молекулы строго ориентированы в одном и том же направлении), то —а2 « T)I. При однородном распределении столкновений по всей поверхности тела можно было бы ожидать, что величина |а2| станет меньше, однако |а2| хотя и зависит от отношения осей эллипсоида, все же не может быть намного меньше своего предельного значения:

— а2<т]1.

Этот результат также согласуется с экспериментами для ПАА и МББА. Согласно второй модели (теория плотных жидкостей), уравнение (7.56) принимает вид

(7.57)

Для этого случая можно также получить соотношение

Л2/Л1 = (Ыа)К (7.58)

Очевидно, что этот результат находится в противоречии с экспе­риментальными данными для ПАА и МББА (табл. 7.1 и 7.2). Можно ожидать, что включение ориентационных флуктуации и молекулярного вращения в эту модель может привести к более высоким значениям т]2, лучше согласующимся с эксперименталь­ными данными.

Перейдем, наконец, к обсуждению температурной зависи­мости коэффициентов вязкости. Хорошо известно, что вязкость изотропной жидкости меняется с температурой приблизительно по закону (см., например, [55])

Л1. = Л0ехр (Е/квТ), (7.59)

Где 0 —энергия активации для диффузии, а г —постоян­ная. Из рис. 7.4 видно, что в случае МББА коэффициенты вяз­кости T]2 и т]3, соответствующие трансляционному перемещению, в первом приближении имеют такую же температурную зависи­мость, как и T]I8 (Е ж 0,3 эВ), а отклонение от нее наблюда­ется вблизи температуры TNi. Поскольку в этой области тем­ператур сильно меняется параметр порядка 5, вероятно, здесь существует более сложная зависимость (чем та, которая описы­вается формулой (7.59)), которая должна учитывать величи­ну S. Температурный интервал, а поэтому и изменение S слишком ограничены, чтобы можно было найти истинную функциональ­ную зависимость, однако предположение авторов работы [171] о том, что выполняется равенство

(Л« — Ли)= Const, (7.60)

Следует исключить (здесь R]Is — вязкость изотропной жидкости, экстраполированная на область температур существования не­матической фазы). Из рис. 7.4, по-видимому, следует, что энер­гия активации, связанная с т]*, больше, чем энергия, соответст­вующая r]is. Как уже отмечалось в связи с данными табл. 7.2, результаты измерения гг для МББА, вероятно, не достоверны из-за того, что нельзя исключить ориентацию директора в потоке. Поэтому мы воздержимся от дальнейшего обсуждения этих дан­ных. Ясно, что необходимы точные измерения коэффициентов вязкости, связанных с трансляционным движением молекул, для соединений или их смесей во всем интервале существования нематической фазы. Если одновременно удастся провести и изме­рение параметра порядка, то можно будет установить зависимость коэффициентов вязкости как от Т. так и от S. В настоящее время это, к сожалению, невозможно.

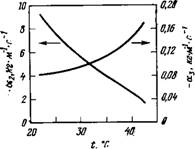
Что касается коэффициентов вязкости Yi и у2, связанных с вращательным движением молекул, то о них имеется несколько более полная информация. Используя данные рис. 7.10 и дан­ные об анизотропии магнитной восприимчивости МББА, можно показать, что зависимость 1п(у1/Д%т) от 1/Т представляет собой прямую линию. Аналогичный результат (рис. 7.11) был получен

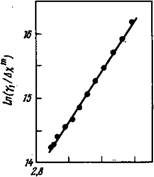
В работе [171] для смеси двух изоме­ров тг-метокси-га’-бутилазоксибензола (N4, Мерк, Дармштадт). У этой смеси довольно широкий температурный ин­тервал существования нематической фазы, в котором величина Д%т меня­ется примерно в три раза, а величина Yi — более чем в 30 раз. Предполагая, как и раньше, что молекула обладает симметрией вращения вокруг своей длинной оси, имеем ~ S, так что Y^Sexp^W). (7.61)

10 3,2 д* Г"7 Ю’3КЧ

Рис. 7.11. Температурная зависимость коэффициента вязкости для соединения N4 [171].

Очевидно, что для коэффициента Yi функциональные зависимости, напри­мер, типа ех?(Е/квТ), S2EE/K*T, S2EES/KBT, SeES/квТ следует отбро­сить. Для МББА величина Е’ « 0.5эВ [89], что несколько выше энергии активации, связанной с вязкостью rjis Для коэффициента Y2 функциональную зависимость от S можно получить следующим образом. Хотя как Yi, так и Y2 не имеют аналогов, относящихся к изотропной фазе, и эти коэффициенты становятся равными нулю при S— 0, выше точки Т = TNi все же сохраняется некоторая ориентация молекул в потоке с градиентом скорости. Этот эффект может быть связан с двумя обстоятельствами. Во-первых, в любой изотропной жидкости, молекулы которой имеют удлиненную форму, оси молекул стремятся повернуться под углом в 45° к направлениям потока и градиента скорости (см., например, мо­нографию Френкеля [55]). Во-вторых, при Т> JTNi может сохра­ниться значительный предпереходный нематический порядок. Сравнение результатов эксперимента по изучению рассеяния света выше TNi С данными для вязкости нематической фазы по­зволяет сделать заключение, что отношение уъ! у, которое опи­сывает ориентацию молекулы в потоке с градиентом скорости, непрерывно при Т = Тт [31]. Поэтому следует ожидать/ что функциональная зависимость Y2 от S такая же, как и у Yv Имура и Окано [84] предложили подробную теорию темпера­турной зависимости коэффициентов вязкости в нематике. Они

Предположили, что тензорные коэффициенты в формальных феноменологических уравнениях гидродинамики нематика мож­но ввести, исходя из тензорного представления параметра по­рядка [уравнение (6.1)]. Используя такой подход, они нашли тензор напряжений Лесли Гуравнение (7.27)] с коэффициентами вязкости, зависящими от S. С точностью до членов второго по­рядка (S2) эти коэффициенты равны

Ах = А^2,

«2 = — (#i + Сг) S — (В2 + С2) S а3 = — (В, — СT)S — (В2 — С2) S2, «4 = 2тц8 — AS + A3S2, (7.62)

"В = ("7"a~Bl) S + (A2~B2)S2′

Новые коэффициенты а, ВCt (I =1,2) представляют собой по­стоянные, которые должны очень слабо меняться с температурой. Соотношение Онсагера — Пароди удовлетворяется для членов каждого порядка по S. Единственный коэффициент, который пропорционален S2, это Действительно, измеренное значение at для МББА оказывается существенно меньше других коэффи­циентов Лесли (табл. 7.2). Уравнения (7.62) содержат только одну энергию активации, одинаковую для нематической и изо­тропной фазы. Следовательно, температурная зависимость ко­эффициентов вязкости, связанных с вращательным движением молекул, согласно этой теории, определяется только темпера­турной зависимостью параметра порядка. Из уравнений (7.62) получаем

Yi = 2CXS -{- 2C2S2, —y2 = 2B1S + 2B2S2, (7.63)

Что находится в противоречии с результатами экспериментов, обсуждавшимися выше.

Соотношения (6.63) были независимо получены Хельфрихом [78], который показал, что должно выполняться равенство = = 0, поскольку величина как обсуждалось выше, должна быть положительной, а параметр S может быть отрицательным, по крайней мере теоретически. Мартине и Диого [141] рассчитали коэффициент Сг на основе молекулярно-статистической теории Майера и Заупе. Они получили

C2~exv(ES/kBT). (7.64)

Приходится констатировать, что все результаты теоретических расчетов довольно плохо согласуются с экспериментальными данными. Хотя таких данных мало, все же найденная экспери­ментально температурная зависимость у^ (см. уравнение (7.61)) позволяет сделать вывод, что

С1~ех?(Е’/къТ), С2ж 0. (7.65)

Поэтому необходимы дальнейшие теоретические исследования.

В ряде экспериментальных работ по исследованию вязкости нематиков ориентация директора не контролировалась [9, 159]. В таких случаях измеряемая эффективная вязкость зависит от угла ориентации директора в потоке. При Т <С величина во> как правило, мала, и можно считать, что измеряется коэффи­циент т)2. Однако при Т ->■ Tni величина 0О может возрастать (рис. 7.6), и измеряемый коэффициент вязкости будет иметь промежуточное значение между значениями rt и т]2. Увеличени­ем 0о можно объяснить рост эффективной вязкости, который часто наблюдается вблизи TNi* Однако отсутствие фактических дан­ных относительно угла ориентации не позволяет проверить спра­ведливость подобного объяснения.

В заключение этой главы сделаем несколько замечаний о ко­эффициентах вязкости смектических жидких кристаллов. Хотя кажущиеся значения этих коэффициентов, измеренные ка­пиллярным методом, очень велики, они не отражают большой величины коэффициентов трения, а обусловлены существованием дополнительного механизма, который называется просачиванием. Этот механизм состоит в том, что в направлении, перпендику­лярном слою, молекулы перемещаются как через Гористую проб­ку, которую они сами же и образуют. При этом определенная роль отводится дефектам. При приближении к фазовому пере­ходу нематик — смектик А предпереходное смектическое упоря­дочение может вызвать расходимость некоторых коэффициентов вязкости аналогично тому, как это имеет место для упругих по­стоянных кручения и продольного изгиба. Очевидно, что резуль­татом такого упорядочения может быть увеличение а1? а3 и ав, но не а2, а4 и а5 [85, 143]. Следовательно, из всех коэффициен­тов Месовича будет изменяться только т]2. Кроме того, будут воз­растать ух и у2. Влияние этого эффекта на величину ^ исследо­валось экспериментально [75]. Даже без подробного обсуждения указанных эффектов ясно, что при экспериментальном изучении «регулярной» температурной зависимости коэффициентов вяз­кости нематика необходимо прежде всего убедиться в отсутствии предпереходного смектического порядка..