До сих пор мы ограничивались рассмотрением проницаемости жидких кристаллов в статических полях. Если внешнее электрическое поле выключить, то ориентационная поляризация будет убывать по экспоненциальному закону в течение некоторого характерного промежутка времени т — времени релаксации. Это означает, что процесс установления равновесной (в отсутствие поля) ориентации собственных дипольных моментов происходит не сразу, а постепенно. Следствием такого процесса является временной сдвиг между ориентацией поля и средней ориентацией дипольных моментов, который имеет место в переменных полях. Этот эффект становится заметным на частотах порядка т"1, а на значительно более высоких частотах ориентационная поляризация вообще не успевает реагировать на изменение поля. В этом случае остаточная проницаемость 8» связана только с наведенной поляризацией. Так как в жидких кристаллах релаксация поляризации зависит от анизотропной проницаемости, то различный характер релаксации ее компонент 8 ц и 8± в принципе дает информацию о динамических свойствах молекул жидкокристаллической фазы.
Чтобы измерить проницаемость на частотах до 10 МГц, можно использовать стандартные емкостные мосты и такую же методику измерений, что и на низких частотах. Однако на высоких частотах следует проявлять осторожность и учитывать возможное влияние сопротивления и индуктивности проводников и электродов, включенных последовательно с измеряемой емкостью и сопротивлением ячейки, включенными параллельно. Это влияние проявляется в том, что измеряемые эффективные значения емкости и сопротивления не соответствуют истинным значениям.
Прозрачные электроды из окиси индия и окиси олова обладают заметным реактивным сопротивлением, и их влияние может оказаться существенным даже при частотах ниже 1 МГц. При частотах выше 10 МГц применяются измерительные цепи не с сосредоточенными, а с распределенными элементами. Часто используются, например, резонансные цепи (см., например, [195]). В работе [40] описана измерительная ячейка для жидкого кристалла, сконструированная на основе коаксиальной линии и пригодная для измерений в области частот выше 10 МГц. Все же измерения проницаемости жидких кристаллов на частотах выше 10 МГц довольно редки, о чем приходится сожалеть, поскольку результаты изучения релаксации на столь высоких частотах могли бы прекрасно дополнить результаты, полученные методами нейтронографии и ядерного магнитного резонанса.
Релаксация поляризующихся изотропных жидкостей может быть описана с помощью обобщенной комплексной проницаемости е* = е’ — ге". В случае переменного поля с круговой частотой со классическая теория Дебая (см., например, [80]) приводит к выражению
Е* («,) = £оо + (е — е<я)/(1 + шт), (5.32)
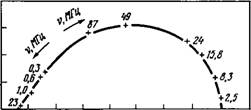
Где & и 8оо — статическая и высокочастотная проницаемости соответственно. Если исключить сот из действительной и мнимой частей уравнения (5.32), можно получить уравнение окружности, и тогда график зависимости е" от е’ должен представлять собой полуокружность. В случае жидкого кристалла это уравнение можно применить к каждой из компонент е* и с_|_. Такие зависимости, называемые диаграммами Cole —Cole, для и-гептил-и’-цианобифенила приведены на рис. 5.6. Для проницаемости е ц действительно получается окружность, а в других случаях наблюдается отклонение, что указывает на существование распределения времен релаксации. Для этого же вещества построена зависимость частоты, соответствующей максимуму потерь (максимуму е"), от величины ИТ (рис. 5.7).
Уравнение (5.32) было впервые выведено Дебаем, который предположил, что выстраивание молекулярных дипольных моментов параллельно приложенному полю нарушается вращательной диффузией. Если обозначить угол между дипольным моментом и внешним полем через 0, то потенциальная энергия молекулы дается формулой (5.4), а вращающий момент равен Г = —DUldQ. Обозначим через /(0, T)DQ долю молекул, диполь — ные моменты которых находятся в телесном угле DQ — 2лзт Ш 0. Учитывая процесс вращательной диффузии, запишем уравнение для /(0, T) следующим образом:
./(6, T) SJ.±(8ine[rffl /(e><)1}t (5.33)
Dt sinfl 90 1 L ДЬ * ВТ ;J)
4-328
Где D — коэффициент вращательной диффузии. Если поле ЕО было включено при T = —оо, то при T = О будем иметь
/(0, 0) =Qexp(— U/KBT)&Q[L + (^£0/А:вГ) cos 9], (5.34)
Где Q — постоянная. Поэтому в случае переменного поля Е = = E0Exip(I(Dt) мы можем искать решение в виде
/(9, t) = Q[i+B{t)^EJkBT)cosQ. (5.35)
Подстановка в уравнение (5.33) дает
В = (1+ «ют’)"1, т’ = 1/2D. (5.36)
8
8
3» *
|
°2 3 4,5 6 6 |
2 0
А
|
2 Ь 6 8 10 |
V V 1,0 0,5
Ч 3
* 2 1 0
6
|
0 5 10 15 Еи |
1’ис. 5.6. Диаграмма Cole — Cole, характеризующая диэлектрическую релаксацию в л-гептил-л’-цианобифениле [125].
Еслц известно /(0, T), можно вычислить ориентационную поляризацию и найти комплексную проницаемость. Обозначив низкочастотный предел через е, а высокочастотный предел через е», получим уравнение (5.32). Соотношение между т и т’ зависит от конкретной модели внутреннего поля.
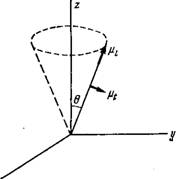
Чтобы понять, что происходит в нематическом жидком кристалле при диэлектрической релаксации, необходимо рассмотреть подробно вклад моментов Р/ и в проницаемости ец и 8j_ соответственно (см. рис. 5.8). Имеем
£ II — £оо II ~ ^ II > = ^ <C0S2 9> + Y A <Sin2 9> ‘
(5.37)
— VL ~ (р±) = ^ (sin2 0) + — <COS20) ,
Где 0 — угол между направлением составляющей и полем. Реориентацию составляющей Xt можно осуществить путем вращения вокруг длинной оси молекулы; это вращение, с точностью до величин первого порядка по Е, не зависит от нематического порядка. Для 8Jl Это основной вклад в процесс релаксации, который, таким образом, не зависит от потенциала поля нематика. Для компоненты ец вклад составляющей дипольного момента fx t в целом менее важен, и, кроме того, он уменьшается с ростом параметра порядка S. Интересное отличие релаксации нематика от релаксации изотропной фазы связано с реориентацией состав-
Рис. 5.7. Частоты релаксации V = 1/2Tct Для и-гептил-л’-цианобифенила.
% экспериментальные значения [32];———————
|
Рис. 5.8. Изменение ориентации компоненты дипольного момента. |
|
3,0 |
|
2,8 |
Теоретические значения (см. текст).
Ляющей дипольного момента i Для поля, направленного вдоль директора (е у), реориентация р t должна осуществляться путем поворота момента вокруг короткой оси молекулы. Потенциал нематика препятствует такому повороту, что приводит к относительно высоким значениям величины т (низкие частоты релаксации). Это легко наблюдать, поскольку среднее значение (cos20) также велико при больших значениях параметра S и составляет основной вклад в величину 8ц. В случае, когда поле перпендикулярно директору (Јi), реориентация р t осуществляется путем поворота на угол я при 0 = const (см. рис. 5.8). Чем меньше угол 0, тем легче происходит такой поворот. В этом случае потенциал нематика приводит к уменьшению времени релаксации (увеличению частоты релаксации). Обычно это трудно наблюдать, поскольку при больших значениях параметра S величина (sin20) мала, и основной вклад в величину е±, который связан с [if, не меняется.
Относительно низкие частоты релаксации поляризации, обусловленной величиной е и нематической фазы, наблюдались различными авторами [133, 5, 174, 1, 96, 8]. Наиболее подходящими соединениями для наблюдения этих эффектов являются соединения, у которых [х = р I и [х t = 0. Частоты релаксации для тг-гептил-тг’-циаиобифенила — соединения, удовлетворяющего этим требованиям, — приведены на рис. 5.7. Когда температура падает ниже значений TNi, сдвиг частоты релаксации действительно происходит в предсказываемом направлении. Можно провести некоторые количественные оценки, предполагая, что потенциал среднего поля в случае нематика имеет вид [ср. с уравнением (1.5)]
W = —gcos20. (5.38)
Тогда в дополнение к электрическому вращательному моменту Г(0) в уравнение (5.33) можно ввести момент TN = 2gsin0cos0. Функцию распределения можно записать в виде /(0, T) = = F(Qy T)W(Q), где м;(0) — функция распределения для нематика в отсутствие электрического поля. Следовательно, получаем дифференциальное уравнение для F( 0, T), решение которого является довольно сложной задачей на собственные значения. Она была решена Мартином, Мейером и Заупе [138]. Полученный ими результат для временной релаксации можно представить в виде произведения так называемых факторов запаздывания на время релаксации для случая, когда потенциал среднего поля нематика равен нулю:
Т7(?)=*7т7(д = 0Ь 7= II, JL — (5.39)
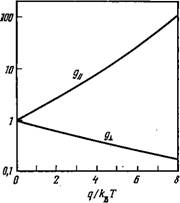
Факторы запаздывания (их не следует путать с корреляционными факторами) зависят от отношения q/kB Т, величины потен
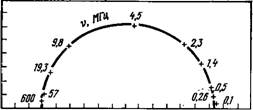
циала поля нематика к температуре (рис. 5.9). Используя молекулярную статистическую теорию Майера и Заупе для нематической фазы (см. гл. 1), можно рассчитать факторы запаздывания для различных значений Q!KB Т и S как функцию приведенной температуры TV2l(TuVm) (см. табл. 5.1). При NI-переходе находим G и =4,0 и GL =0,52, что хорошо согласуется с экспериментальными значениями 4,2 и 0,55 (рис. 5.7). Штриховая линия, показанная на рис. 5.7, была рассчитана исходя из экстраполированного значения частоты релаксации для изотропной фазы; использованные значения и g± приведены в табл. 5.1, а значения плотности взяты из работы [42].
Из экспериментальных данных, приведенных на рис. 5.6, видно, что для ец действительно имеется единственное макроскопическое время релаксации, а в случае г± времена релаксации дипольных моментов молекул распределены по широкому интервалу значений. Зависимость е1(е1) соответствует трем процессам релаксации дебаевского типа. Наиболее важный из них можно идентифицировать как вышеописанную запаздывающую релаксацию. Второй процесс — это релаксация на более низких частотах (того же порядка величины, что и в случае ец), третий процесс соответствует высоким частотам. До настоящего времени нет определенного мнения относительно механизмов, ответственных за эти процессы релаксации.
Таблица 5.1
Факторы запаздывания, рассчитанные с использованием среднего
|
Рис. 5.9. Зависимость факторов запаздывания от амплитуды нематического потенциала [138]. |
__________ Нематического потенциала Майера — Заупе_______________
|
TVV(Tm V2ni) |
S |
Ё II |
|
|
1 |
0,429 |
4 |
0,52 |
|
0,985 |
0,479 |
5 |
0,48 |
|
0,970 |
0,516 |
6 |
0,43 |
|
0,941 |
0,569 |
8,2 |
0,39 |
|
0,912 |
0,610 |
11 |
0,37 |
|
0,884 |
0,643 |
15 |
0,35 |
Предпринимались различные попытки вычисления величины Dy которую связывали с коэффициентами вязкости (см., например, [80]). При экстраполяции частоты релаксации поляризации изотропной фазы на область температур существования нематической фазы мы предположили, что D не претерпевает разрыва в точке Т = TNi и что температурная зависимость D в изотропной и нематической фазах одна и та же. Это означает, что величина D зависит от локальной, определяемой близкодействующими силами структуры жидкости и не зависит от нематического потенциала. Поскольку теоретические и экспериментальные значения факторов запаздывания G\ и GL в точке Т = согласуются почти идеально, то, по-видимому, первое из предположений правильно. Расхождение между результатами расчетов и экспериментов, увеличивающееся при понижении температуры, возможно, связано с нарушением второго предположения.
В настоящее время нет других экспериментальных результатов для соединений Ср=р/ир^=0. Если р T Ф 0, то интерпретация процесса релаксации сильно усложняется. В этом случае т(Q = 0) нельзя уже отождествлять со значением для изотропной фазы т15, а это затрудняет определение факторов запаздывания [157, 148, 182]. Если тем не менее использовать Xis для расчета как было сделано Мейером и Заупе [145] для ПАА, то получается неправильное значение намного
Превышающее предсказания теории.
При обсуждении диэлектрической релаксации нематиков не осуществлялось явное решение дифференциального уравнения для нахождения функции распределения. Вместо этого функция распределения выбиралась в виде F(0, 0)=1+а(/?, Z)cos0.
При этом для G|| было получено выражение
G, = (kT/q) [exp (q/kBT) — 1]. (5.40)
Обычно Eq,KBTИ последнее слагаемое можно опустить. Значение рассчитанное с помощью уравнения (5.40),
Примерно вдвое выше, чем приведенное на рис. 5.9. Для изотропной фазы часто оказывается, что время релаксации т(Q = 0) пропорционально вязкости ц жидкости. Поскольку температурную зависимость вязкости можно описать с помощью формулы ц ~ exp(gvisc//cB Т), из уравнения (5.40) получаем
■ т,(?) ~ Exp [(q + qV[SC)/kBT. (5.41)
Хотя A Priori не ясно, какую из вязкостей нематика нужно использовать (см. гл. 7), оказалось, что уравнение (5.41) описывает результаты ряда экспериментов при величине, равной Q « ^ 30—50 кДж/моль [96]. Низкие частоты релаксации (в области частот порядка кГц), найденные для некоторых случаев, обязаны своим происхождением комбинации высокой вязкости [уменьшающей т(Q =0)] и низкой приведенной температуры Т/Тщ (увеличивающей Q и, следовательно,
Особенный интерес представляет случай, когда величина Де вначале положительна. Релаксация поляризации, обусловленная проницаемостью е ц, может тогда привести к изменению знака Ае в области частот порядка кГц, легко доступной экспериментально. Это открывает возможность исследования поведения нематиков во внешних электрических полях в зависимости от анизотропии диэлектрической проницаемости [94].
Таким образом, обобщение на случай нематиков уравнения Дебая, учитывающего вращательную диффузию, довольно хорошо описывает экспериментальные данные. Это уравнение приемлемо для описания релаксации в соединениях, образующих жидкие кристаллы, по-видимому, потому, что их молекулы не могут ни свободно поворачиваться, ни менять ориентацию мгновенными скачками. Теория, включающая подобные модели поворота молекулы, была развита в работе [126]. Поскольку ближний порядок в изотропной и в нематической фазах примерно одинаков, все мыслимые типы поправок будут в первом приближении для обеих фаз одинаковыми. Различие процессов релаксации в этих двух фазах следует отнести за счет нематического потенциала. Поэтому можно ожидать, что, несмотря на ограничения модели Дебая, расчет факторов запаздывания проведен правильно. Чтобы рассчитать абсолютные значения Тц и т±, нужно вычислить значения D и внутреннего поля для определенной модели, точно так же как и при расчете т для изотропной фазы.
 19 января, 2013
19 января, 2013  admin
admin 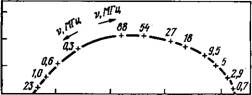
 Опубликовано в рубрике
Опубликовано в рубрике 