При исследовании диэлектрических свойств вещества изучают его реакцию на внешнее электрическое поле. В классическом эксперименте исследуемым веществом заполняют конденсатор и определяют увеличение его емкости от значения С до значения гС, где е — относительная проницаемость вещества. Увеличение емкости вызывается поляризацией вещества в поле Е, состоящей в том, что положительные заряды притягиваются к одной пластине конденсатора, а отрицательные — к другой. Для анизотропного вещества поляризация, относимая к единице объема, определяется формулой (4.5). Используя соотношение (4.6), получаем[5]
P = e0(t—1)£. (5.1)
Вещества, образуемые неполярными молекулами, обладают только наведенной поляризацией, которая складывается из электронной (существующей, в частности, и в оптическом диапазоне частот) и ионной поляризации. У веществ с полярными молекулами наряду с наведенной поляризацией наблюдается также ориентационная поляризация, вызванная стремлением собственных дипольных моментов молекул ориентироваться параллельно приложенному полю. Так как проницаемость изотропных жидкостей и газов изотропна, то тензорную величину (е — I) в выражении (5.1) можно заменить на скалярную величину е — 1. В то же время в твердых телах, проницаемость которых, как правило, анизотропна, ориентация собственных дипольных моментов в поле Е практически не меняется, и поэтому вклад ориентационнрго механизма поляризуемости в проницаемость оказывается не столь существенным. В случае жидких кристаллов дело обстоит гораздо сложнее, поскольку теперь анизотропная проницаемость характеризует не твердое, а жидкое состояние вещества. Поэтому при наличии полярных молекул вклад ориентационной поляризации в анизотропную проницаемость жидких кристаллов является существенным.
Ограничимся рассмотрением одноосной жидкокристаллической фазы и введем систему координат (я, у, Z) таким образом, чтобы ось Z была направлена вдоль директора. Тогда главные
компоненты тензора г можно записать так: ец = е22 и ej_ =
= — т> + Для измерения величин ец и Ej^ обычно
|
C7HI5-@-N
|
|
ZrN-ф—ОСН3 О |
|
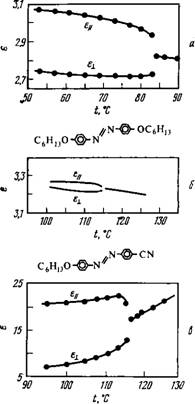
Рис. 5.1. Диэлектрические проницаемости п, д’-дпгептилазобензола (а) [88] и ПАА (б) [131]. |
Используется плоский конденсатор, емкость которого измеряется на переменном токе определенной частоты (например, 1 кГц). Частота выбирается достаточно низкой, чтобы измеряемую проницаемость можно было по существу считать статической, и достаточно высокой, чтобы избежать протекания электрохимических реакций и образования двойных слоев на электродах. На практике часто используется ячейка типа применяемых в дисплеях, которая представляет собой две стеклянные пластины, снабженные точно изготовленными электродами и удерживаемые на небольшом расстоянии друг от друга с помощью дистанциона — торов. Паразитную емкость Ср находят в результате градуировки, для которой используется диэлектрическая жидкость с известной проницаемостью. Для измерения величины ец или необходимо установить ориентацию поля соответственно параллельно или перпендикулярно направлению директора. Это возможно, если ячейка тонкая, например <^100 мкм при гомео — тропном и планарном типах упорядочения. Чтобы можно было
проверить однородность получаемой таким образом структуры, необходимо использовать прозрачные электроды. Однако обычно предпочитают ориентировать директор магнитным полем, что позволяет измерить обе величины ец и е± при одной и той же ячейке д тем самым повысить точность определения разности Де = б || — е±. В таких экспериментах образцы жидких кристаллов должны быть не слишком тонкими (примерно ^>160 мкм для магнитных полей напряженностью ~800 кА/м), чтобы можно было пренебречь влиянием граничных слоев жидкого кристалла, в которых направления директора и поля не полностью совпадают. Приложенное напряжение во всех случаях должно быть небольшим «1 В), чтобы избежать появления электрогидродинамических неу стойчивостей, которые могут нарушать однородную ориентацию директора.
Экспериментальные данные для б || и Ej_ неполярных соединений (для которых Де>0) и полярного соединения ПАА в нематической фазе приведены на рис. 5.1. В последнем случае ориентационная поляризация дает больший вклад в величину еj_, чем в ец, что приводит к отрицательному знаку разности Де. На практике можно получить довольно большие значения |Де|, которые зависят от величины полного диполь — ного момента х и угла между [I и длинной осью молекулы (рис. 5.2). Величина Де обычно зависит от температуры. Данные о проницаемости различных жидких кристаллов приводятся в обзорах [18, 88].
Задача теоретического опцсация диэлектрической проницаемости жидких кристаллов, состоит в объяснении
|
|
|
C7hi5-^®-cn |
|
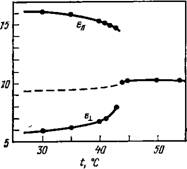
Рис. 5.2. Диэлектрические проницаемости некоторых соединений с большой положительной (в) и большой отрицательной ДО анизотропией диэлектрической проницаемости. |
3"
их макроскопической анизотропии на основе анизотропии молекул при наличии неполного ориентационного порядка. Оказывается, что такое описание легко выполнить. Гораздо труднее сделать обратное, т. е. определить молекулярные характеристики по наблюдаемой макроскопической проницаемости. У полярных молекул может существовать специфическое взаимодействие дипольных моментов, и это сильно усложняет задачу. Кроме того, информация о соответствующих свойствах молекул, полученная независимыми методами, оказывается недостаточной, чтобы можно было судить о правильности различных возможных приближений. Тем не менее, как будет показано, исследования диэлектрических свойств часто дают важное качественное представление о межмолекулярных взаимодействиях.
Для неполярных соединений рассмотрение проводится относительно просто. Используя результаты, приведенные на рис. 5.1, а, можно показать, что для п, п’-дигептил азобензол а Де ~ аналогично тому, как в оптическом диапазоне частот п — ~ (гл- 4). Это означает, что все рассуждения, приведенные в предыдущей главе, применимы и в данном случае, и можно воспользоваться уравнениями (4.29), чтобы связать е с тензором поляризуемости а молекулы, который теперь, однако, должен учитывать и вклад ионной поляризуемости. Таким путем для полной статической поляризуемости п, тг’-дигептилазобен — зола получаем
А, = 99,3, At = 46,8 (10~40 Ф*м2).
Эти значения можно сравнить с найденными в результате измерений показателей преломления (табл. 4.1) и экстраполяции данных к X =оо. Вклад ионной поляризуемости Aznat оказывается равным ~10 и ~4 (10~40 Ф-м2) соответственно, т. е. он, как обычно и предполагают, составляет около 10% от полной величины.
Для полярных молекул в (4.14) нужно добавить ориента — ционную поляризацию
P = N((* •£г) + (7», • (5.2)
Где |и — среднее значение дипольного электрического момента в присутствии электрического поля, а угловые скобки означают усреднение по всем ориентациям молекул. Из выражений (5.1) и (5.2) имеем
(е _ I) . £ = (N/е0) (<« • Е%) + <£». (5.3)
Майер и Мейер [130] получили соотношение (5.3) для нематиче — ского жидкого кристалла в рамках теории Онсагера для изотропной фазы. Поэтому вначале приведем результаты для изотропной фазы. Детальный расчет и более подробное обсуждение даются в работе [17].
Чтобы найти ориентационную поляризацию в изотропной фазе, значение Ji вычисляют, исходя из выражения для энергии диполя в ориентирующем поле Ed
U = — ji • Ed = —[x^cosG, (5.4)
Где 0 — угол между направлениями Ed и ji. Среднее значение cosQ определяется с помощью известной функции Ланжевена, и если в разложении в ряд (по отношению U/ks Т) ограничиться только первым слагаемым, то получим
{It = jTc^se = [ц2/(3/гвГ)] Ed. (5.5)
Для вычисления проницаемости конденсированной фазы нужно наряду с полем Ed учесть и поле Et. По Онсагеру, внутреннее электрическое поле Et отличается от ориентирующего из-за наличия поля реакции. Диполь поляризует свое окружение, которое и создает поле реакции R в месте расположения данного диполя. Поскольку поле R всегда параллельно диполю, оно не может ориентировать диполь, но дает вклад в величину Et. Внутреннее поле равно сумме ориентирующего поля Ed и среднего поля реакции JR:
TOC o "1-3" h z Et=Ed+R. (5.6)
Поле реакции дипольного момента Ji молекулы с поляризуемостью а равно
/?=/(,I + A/?)=/F|I, (5.7)
Где / — фактор поля реакции, который для сферической полости радиуса а выражается следующим образом:
/==(в-1)[27гв0а3(2е + 1)Г1, (5.8)
А
^=(1— /а)-1. (5.9)
Ориентирующее поле Ed в свою очередь равно сумме двух полей: поля в сферической полости
Ес = [3s/(2s + 1 )]E=HE (5.10)
И поля реакции наведенного дипольного момента. Это дает
Ed=Ec+f*Ed=FhE. (5.11)
С помощью формул (5.5), (5.6) и (5.11) можно рассчитать Et и Ed. Подставляя результаты в основное уравнение (5.3) и заменяя тензор я его средним значением а, получаем формулу Онсагера
В = 1+ (NhFIЕ0) [а + FFx2/(З&в Г)]. (5.12)
Величины H и F зависят от е и а и от радиуса а сферической полости, который обычно выбирают так, чтобы выполнялось равенство
—J TzNa3 = 1. (5.13)
Используя это соотношение и значение а, полученное для ВЧ — проницаемости е<» [формула Клаузиуса—Мосотти, уравнение (4.26)], можно переписать уравнение (5.12) в виде
2е + е Д7
(е — SQq)—— = ————— £—- fx2. (5.14)
«(«оо + 2)а 9ео*вГ
С помощью уравнения (5.14) можно рассчитать величину собственного дипольного момента молекулы, исходя из диэлектрической проницаемости, если известны плотность и значение е». Сравнение с реальными значениями Fx, найденными по данным для газовой фазы, позволяет проверить справедливость допущений, принятых при выводе уравнения (5.14) [см., например, табл. 16 в работе [17]. Расхождений можно ожидать, если молекулы нельзя считать сферическими или если между ними имеется специфическое взаимодействие. К сожалению, часто бывает трудно определить, какой именно фактор является ответственным за наблюдаемое расхождение.
Теперь перейдем к обобщению теории Онсагера на случай нематического жидкого кристалла, сделанному в работе Майера и Мейера [160]. Будем считать молекулу анизотропно поляризующимся точечным объектом (главные значения тензора поляризуемости л равны а1 и At) в сферической полости радиуса А. Такая молекула, кроме того, имеет собственный дипольный момент ji, составляющий угол Р с направлением аг Поэтому HJ = fxcosp и fxf = fxsinp. Далее в работе [160], как и в теории Онсагера, приняты следующие допущения: при расчете коэффициентов H и / анизотропия проницаемости не учитывается и в выражениях (5.10) и (5.8) е заменяется на е (это допущение справедливо, если Ае е); при расчете множителя F анизотропия поляризуемости не учитывается и в соотношении (5.9) а заменяется на а (в действительности это допущение некорректно, поскольку разность al — at имеет тот же порядок величины, что и a t).
Эти допущения означают, что поля Et и Ed считаются изотропными, как и в приближении Вукса для неполярных
Молекул. По аналогии с этим приближением напишем для наведенной поляризации [см. уравнение (4.14)]
Р = N (а) Ег (5.15)
И, используя соотношения (3.19), получим
<*>, = M2S + 1) + я,(2-:25)],
<«>х=Т Ml-S)+M2 + S)].
Расчет ориентационной поляризации производится следующим образом. Полная энергия молекулы равна U + W, где W — Потенциал, создаваемый молекулами нематика, a U — потенциальная энергия дипольного момента в электрическом поле [определяемая формулой (5.4)]. Разлагая по U и ограничиваясь слагаемым, линейным по электрическому полю, получим
Exp [—(U + W)/KB Г] « (1 — U Ik в Т) ехр (— W/KB Т). (5.17)
Тогда средние значения дипольных моментов JnT (Y = || , J_) в электрическом поле определяется формулой
<Рт> = <t (1 + V)> = Оф Е*1 кът- (5.18) Компонента диполя вдоль оси z равна
(X J = |ы/ cos Э + |Ltf sin г|) sin 6 , (5.19)
Где г|) — угол между плоскостью (|ы, С) и нормалью к плоскости (z, О (ср. рис. 1.4). Используя это выражение для (Ыц и учитывая, что (sin2!])) = 1/2 (вследствие того, что молекула по предположению аксиально-симметрична), получаем
<ц2, > = I*? <cos« е> + — i — ^ <sin« в> =
= ± [nf(2S + l) —S)] =-|- ц2 [ 1 — (1 — 3 Cos2 р) 5]. (5.20а)
Аналогичный расчет дает
(V& =—F [ £ (1 — S) + —J— £ (2 + S)] =
= _L ^ Jl + — L (1—3cos*0)S]. (5.206) При S = 1 в величину (ц.2ц) вносит вклад только компонента
Fa г ив (fix) — только их-
Иснользуя выражения для Ei и Ed, как в изотропном случае, можно записать уравнение (5.3) в виде
Вт = 1 + (NhF/S0) (<«)т + F )/ fcBD, V = II, ±, (5.21)
Где (а)т дается формулами (5.16), A — формулами (5.20). Из уравнений (5.21) получаем анизотропию электрической проницаемости
Де = (7VftF/s0) — at — F (Р*/2КвТ) (i — 3cos2p)]S. (5.22)
Если |ы == 0, уравнения (5.21) сводятся к системе уравнений (4.25). Это можно проверить, подставив в уравнения (5.21) выражения (5.10) и (5.9) для H и F соответственно (предварительно заменив е и а на е и а) и использовав соотношение (5.13). Как уже отмечалось, допущения Майера и Мейера аналогичны допущениям, сделанным при рассмотрении случая изотропного внутреннего поля в приближении Вукса. Более того, если вычислить величину е, то получим формулу Онсагера (5.12), в которой е будет заменено на е. При S = 0 уравнения (5.21) также сводятся к уравнению Онсагера. Поэтому теория предсказывает непрерывность е при Т = Гш (если не учитывать небольшое изменение е, связанное с изменением плотности). В отличие от нематиков, состоящих из неполярных молекул, это предсказание теории экспериментально не подтверждается. Отметим, наконец, что в другом предельном случае, 5=1, теория предсказывает конечный вклад ориентационной поляризации в проницаемость. На практике вращение молекулы вокруг короткой оси затрудняется по мере приближения S к единице. Это означает, что частота релаксации, связанная с е ц, смещается в область все более низких частот (разд. 5.2). Подобный эффект связан с динамикой процесса и не нарушает справедливости статической теории.
На первый взгляд кажется заманчивым обобщить модель сфероида, с помощью которой получены соотношения (4.29), на случай полярных молекул. Однако в последнем случае в отличие от предыдущего (неполярные молекулы) мы не располагаем экспериментальными данными, которые свидетельствовали бы о независимости Et и (или) Ed от макроскопической анизотропии диэлектрической проницаемости. Следовательно, для указанного обобщения теории Майера и Мейера нужны специальные допущения, справедливость которых трудно проверить. Допущения Держанского и Петрова [34] в рамках модели сфероида нельзя считать верными, так как теория, развитая на их основе, не предсказывает непрерывности величины е/р в точке NI-перехода при р, == 0.
Уравнения Майера и Мейера удовлетворительно описывают многие существенные особенности проницаемости нематических жидких кристаллов, образуемых полярными молекулами. Лучше всего это проиллюстрировать с помощью соотношения (5.22) для разности Де. Если 3cos2P = 1 (Р « 55°), дипольный момент вносит одинаковый вклад в величины ец и е±. При этом Де определяется (положительной) анизотропией поляризуемости. Вклад диполя в Де положителен для р< 55° и отрицателен для Р>55°. В последнем случае знак Де зависит от относительной величины двух вкладов: вклад наведенной поляризации в Де меняется с температурой подобно параметру порядка S; температурная зависимость ориентационной поляризации определяется отношением SIT. Остальные виды поляризации слабо зависят от температуры. Рассматриваемый подход позволяет прекрасно объяснить следующие экспериментальные данные.
Если величина Де отрицательна или положительна и велика, то пропорциональность Де величине S/T, связанная с вкладом дипольного момента, преобладает во всей области температур. Следовательно, |Де| растет с уменьшением температуры (рис. 5.1, б, 5.2, а и 5.2, б).
Если величина Де положительна и близка к нулю, анизотропия наведенной поляризации примерно равна анизотропии ориентационной поляризации. Ниже точки Т = 7ni и вблизи нее определяющей является температурная зависимость параметра S и Де растет с уменьшением температуры. При более низких температурах изменения S малы, и преобладающей является зависимость S/T, связанная с ориентационной поляризацией. Тогда может оказаться, что с уменьшением температуры величина Де сначала растет, затем проходит через максимум и падает (рис. 5.3, б).
Количественно более точно проверить формулы (5.21) и (5.22) трудно. Для ПАА информацию об сс и сс I — ос f можно получить из результатов оптических измерений. Воспользовавшись уравнением Онсагера и уравнением (5.22), можно найти сначала р, = = 7,4-10~30 Кл-м[6], а затем р =65° (эти значения получены для величины е, равной проницаемости изотропной фазы). Приведенный результат для р, довольно хорошо согласуется с величиной 7,7-10~30 Кл-м, найденной для разведенных растворов ПАА в бензоле [131], а оба значения (р и Р) — с данными, полученными на основе результатов измерения постоянной Керра. Однако, как уже отмечалось, такое согласие не обязательно подтверждает правильность принятых допущений.
В качестве примера того, как можно использовать (по крайней мере качественно) уравнения (5.21) и (5.22), обсудим влияние
концевых групп на проницаемость п, и’-замещенных азобензолов. На рис. 5.1, а приведена температурная зависимость проницаемости п, я’-дигептилазобензола. Это вещество неполярно, и поэтому его можно использовать для сравнения (в качестве «точки отсчета»). На рис. 5.3 приведены аналогичные зависимости для некоторых азобензолов с различными сочетаниями концевых групп. Сравним сначала данные рис. 5.1, а и рис. 5.3, а. Замещение одной гептильной группы на алкоксигруппу близкого размера приводит к небольшому увеличению как 8ц, так и е1. При температуре, равной 0,97 TNi» значение Де
Меняется с 0,4 на 0,3. Диполь-
Ный момент группы —ОСН3 равен 5,6-10~30 Кл-м и составляет угол в 72° с пара-осью соседнего ароматического кольца [147].
Предположим, что это значение момента является типичным для алкильных цепей, более длинных, чем — ОСН3. Продольная компонента дипольного момента алкокси-группы (1,73-10~30 Кл-м) противоположна диполь — ному моменту гептильной группы, равному около 1,3-10~30 Кл-м вдоль пара-Оси. Однако полного погашения момента, как в случае диалкильного замещения, здесь ожидать нельзя. Кроме того, поляризуемость вдоль пара-Оси несколько больше, чем в случае диалкильного замещения. Эти два эффекта объясняют увеличение проницаемости е ||. Увеличение же проницаемости ех обусловлено поперечной компонентой дипольного момента алкокси — группы.
|
/М-®-ОС6Н13 |
|
C7H15^N( |
|
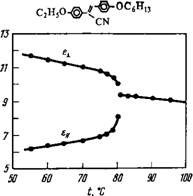
Рис. 5.3. Диэлектрические проницаемости некоторых азобензолов с замещенными концевыми группами [88]. |
Если введены две алкокси — группы (рис. 5.3, б), то поперечная компонента полного дипольного момента примерно в 1 2 раз больше, чем в случае рис. 5.3, а (при свободном вращении алкокси-групп склады-
Ваются квадраты дипольных моментов). Однако, поскольку ец также несколько увеличивается вследствие большей поляризуемости вдоль пара-Оси, разность Де по-прежнему положительна (но мала). Наконец, рассмотрим случай замещения концевой группы цианогруппой (рис. 5.3, в). У цианогруппы большой дипольный момент (13,5-10~30 Кл-м) направлен вдоль пара-Оси. Вклад этого дипольного момента в проницаемость превышает вклад всех остальных молекул. Поскольку угол между пара- Осью и осью С молекулы мал, проницаемость ец велика и, следовательно, анизотропия Де имеет большое положительное значение. Величина е падает с уменьшением температуры (рис. 5.3, в), что отличает наблюдаемую температурную зависимость от обычной и находится в противоречии с поведением, которое предсказывается уравнением (5.12). Такой эффект типичен для веществ, у которых дипольные моменты складываются антипа- раллельно. При низких температурах происходит более полное погашение моментов.
Приведенное рассмотрение оказывается очень полезным для описания анизотропии диэлектрической проницаемости вещества по данным о значениях дипольных моментов отдельных групп. К настоящему времени опубликованы сравнительные данные о значениях диэлектрической проницаемости для различных шиф — фовых оснований и фенилбензоатов [108], для различных мости — ковых групп [97] и других молекулярных структур [132, 37, 182, 107, 109, 110].
Существенное расхождение между теорией Майера и Мейера и экспериментом состоит в том, что при Т = 7Ni С ДЛЯ нематической фазы всегда ниже значения е для изотропии фазы. Будем обозначать разность этих значений через бемь Исследование различных соединений показывает, что 6Cni не зависит от знака и величины Де. В принципе этот эффект можно объяснить либо тем, что при расчете Et и Ed не учитывалась анизотропия нематика, либо тем, что при Т = Т^х имеет место систематическое изменение специфического межмолекулярного взаимодействия. Поскольку Де слабо влияет или вообще не влияет на величину бемь второе предположение кажется более вероятным, чем первое. Несколько примеров этого эффекта будут рассмотрены в конце раздела.
В теории Онсагера исследование диэлектрических свойств полярных жидкостей проводится на основе рассмотрения поведения некоторой молекулы в среднем поле других молекул. При этом принимается, что окружение рассматриваемой молекулы является сплошной средой, а короткодействующие силы можно не учитывать. Для изотропных полярных жидкостей принципиальную возможность учета таких сил дает теория Кир- квуда—Фрелиха [17, 14]. В ней проводится статистическое рас
смотрение молекул, находящихся в малом, но еще макроскопическом сферическом объеме и, погруженном в бесконечный диэлектрик с проницаемостью е. В таком случае проницаемость можно связать с полным электрическим моментом шара. Расчет среднего значения этого момента дает
(е-е~)77ГТ1^ = (9е<ЛвГ) 1 <22>*J> =
I ОО "+" I j
-1
Оо
= [JV/(9e0*Br)]^. (5.23)
Здесь G — корреляционный фактор Кирквуда, а суммирование проводится по всем молекулам, находящимся внутри сферы. Множители при е — e^ связаны с решением электростатической задачи о поляризации шара с проницаемостью 8», находящегося в диэлектрике с проницаемостью е, и о напряженности поля в полости в этом шаре. В отличие от теории Онсагера выражения (5.23) являются точными, если шар имеет макроскопические размеры. В отсутствие корреляций G = 1 и уравнение (5.23) сводится к уравнению Онсагера (5.14). Чтобы вычислить G для реальных условий, нужны специальные допущения о межмолекулярных взаимодействиях в рассматриваемых системах.
|
|
|
= (9T0kBTv)-* <2 S (Pi)T Ыт> = l^cWl g, <H?>, V = ||, J_, (5.25) |
Для обобщения уравнения (5.23) на случай жидких кристаллов рассмотрим макроскопическую сферу в одноосном анизотропном диэлектрике с проницаемостями 8ц и е±. В рамках такой модели можно найти напряженность поля внутри полости и решить связанные с таким расчетом задачи так же, как в случае изотропных жидкостей. Для этого надо осуществить следующее преобразование:
Х’=хгIV y’=yel4′, z’=ze7v«. (5.24)
В этих новых координатах сфера преобразуется в сфероид с отношением осей (£ц/е±)1/2> и коэффициенты деполяризации будут зависеть от анизотропии диэлектрической проницаемости» Чтобы отличать эти коэффициенты деполяризации от рассмотренных ранее (введенных для молекулярного сфероида), обозначим их через Q^(Y = //, _|_). Если при расчете момента шара для внутреннего поля использовать формулу Вукса, то уравнение Кирквуда—Фрелиха для анизотропного случая примет вид [17]
Где определяется уравнениями (5.20). Если для расчета внутреннего поля использовать сфероидальную модель, то получится уравнение, незначительно отличающееся от уравнения (5.25) [16]. Поэтому проведем обсуждение двух различных примеров корреляционных эффектов на основе уравнения (5.25).
|
|
|
C7h15-®-n |
|
//м-ф-с7н15 |
|
50 60 T,’C |
|
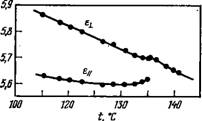
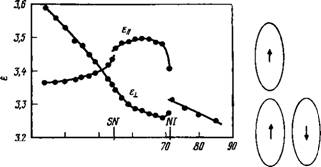
Рис. 5.4. Диэлектрические проница — Рис. 5.5. Корреляция дипольных емостн и, и’-дигептилазоксибензола моментов соседних молекул. [88]. |
Влияние смекщического порядка. Статическая проницаемость п, n’-дигептилазоксибензола в изотропной фазе, нематической фазе и смектической фазе А приведена на рис. 5.4. Ниже температуры 7Ni И вблизи нее величина Де, как обычно, растет с уменьшением температуры, затем падает и наконец Де меняет знак. Сравнение с другими соединениями ряда показывает, что такой эффект связан с появлением смектической фазы [96], в которой взаимодействие дипольного момента с диполями окружающих молекул иное, чем в нематической фазе, из-за неизотропного распределения центров масс молекул. Для диполей, расположенных в центральной части молекулы, расстояние до диполей молекул соседних слоев гораздо больше, чем расстояние между соседними диполями в одном и том же слое. Для компоненты диполя, направленной вдоль директора, это приводит к усилению антипараллельной корреляции (рис. 5.5). Следовательно, эффективный момент в этом направлении уменьшается, что приводит к падению ец. Аналогично можно объяснить увеличение е±.
|
|
Заметим, что, поскольку среднее значение диполя Fi в электрическом поле пропорционально р,2 [согласно уравнению (5.5)], вращение молекул вокруг длинной или короткой оси не меняет
Этого результата. Так как переход нематик — смектик А в п, п!- Дигептилазоксибензоле близок к переходу второго рода (скрытая теплота превращения очень мала),, уже в нематической фазе сильно проявляются предпереходные эффекты, связанные с появлением смектического порядка. В этом случае правую часть уравнения (5.35) можно вычислить следующим образом. Будем считать, что некоторая молекула сфероидальной формы, имеющая длинную ось 2а и короткую ось 26, находится внутри малой, но все же макроскопических размеров сферы. Среднее значение момента сферы в поле центрального диполя равно |ы. Ограничимся рассмотрением компоненты р, ц, которую можно вычислить весьма приближенно, предполагая порядок идеальным (S = 1) и принимая радиус сферы равным а. Средний момент частицы, находящейся на расстоянии г от фиксированной молекулы, примем равным (ы2ц E(R)/KB Т, где Е(г) — поле центрального диполя [ср. с уравнением (5.5)]. Тогда в случае нематика
Ji„ (nem) =fi„ + (ЛЦ / квТ) j EdV , (5.26)
Где интегрирование проводится по объему шара, не занятому молекулярным сфероидом, а N = 3/(4 Nab2) — плотность диполей. В результате интегрирования получаем
JЈdF = — Q|1 (5.27)
Где коэффициент деполяризации Qg, определяемый уравнением (4.12), для шара равен Va, а для сфероида с а >& йц < « 1/3. Тогда
^(Nem)*^-^/ *Br)(4«„abV]. (5-28)
Для смектической фазы А предположим (в дополнение к условию S = 1), что центры масс молекул точно расположены в параллельных друг другу слоях. Интегрирование по объему шара при этом сводится к интегрированию по площади круга (обозначим ее через Q):
Р „ (sm) = fi „ + (AVu / V) j Eda • <5’29>
Здесь N‘ = I/(Nb2) — поверхпостная плотность диполей. Поскольку
J EdQ = ([i „ 12e0) (1 La —1 /B), (5.30)
При A B находим
(Sm) = ц [1-(v/kBT) (2те0Ь3)-1]. (5.31)
Сравнение уравнений (5.28) и (5.31) показывает, что для смек — тической фазы поправочный множитель к рц в 2а/B « 10 раз больше соответствующего множителя для нематика. В дейстэи — тельности найденные таким образом поправки слишком велики, что не удивительно, если вспомнить, какие допущения были сделаны при их вычислении. Тем не менее расчеты показывают, что G и < 1, причем в согласии с экспериментом у смектиче — ской фазы gц значительно меньше, чем у нематической. Аналогичным образом можно показать, что Ј_L>1.
Ассоциация в пара-цианозамещенных соединениях. У нематической фазы и-гептил-тг’-цианобифенила из-за относительно боль-г шой величины момента цианогруппы, параллельного длинной оси молекулы, наблюдается большая положительная анизотропия диэлектрической проницаемости (рис. 5.2, б). Значения е для нематической и е для изотропной фаз увеличиваются с ростом температуры. Расчет корреляционных факторов дает значение gк, которое значительно меньше единицы, что свидетельствует о сильной антипараллельной корреляции дипольных моментов. По-видимому, ассоциация диполей в таких существенно полярных веществах оказывает сильное влияние на свойства жидкокристаллической фазы. В этой связи можно, например, привести следующие особенности подобных соединений.
1. П, п’-замещенные бифенилы имеют смектическую фазу почти при всех обычных замещениях концевых групп. Нематиче- ская фаза появляется только в тех случаях, когда присутствуют сильно полярные концевые группы (—CN, —NO2 и т. д.) [185, 63].
2. Если мезогенное соединение с сильно полярной концевой группой имеет смектическую фа§у, то молекулярная толщина слоя обычно в 1,4 раза превышает длину вытянутой молекулы. Поэтому образуются двойные слои нескольких типов (см., например, [115]).
3. Бинарные смеси мезогенного соединения, обладающего сильно полярной концевой группой, и соединения, в которых такая группа отсутствует, обладают весьма специфическими фазовыми диаграммами. Часто в области концентраций 1 : 1 образуется устойчивая смектическая фаза, даже если чистые вещества вообще не имеют смектических фаз [153].
4. Если одно или оба фенильных кольца в п, п — замещенных бифенилах заменены циклогексановыми кольцами, то и в этих случаях проявляются свойства нематической фазы, но только при наличии сильно полярной концевой группы [47].
Перечисленные эффекты в значительной степени неожиданны, если исходить из сведений, получаемых в экспериментах с традиционными мезогенными соединениями. Очевидно, что фактором, определяющим появление таких эффектов, является степень ассоциации диполей, связанная с сильно полярными группами. Поэтому методы изучения диэлектрических свойств, вероятно, могут быть очень полезными для достижения лучшего понимания неизвестных эффектов.
Интересные корреляционные эффекты иного рода наблюдаются на N-замещенных бензойных кислотах, которые существуют в основном в виде димеров [110]. Однако все подобные случаи показывают, что корреляция дипольных моментов может играть очень важную роль в формировании свойств рассматриваемых соединений. Наблюдаемые значения 6eNi, вероятно, могут быть связаны со скачкообразным изменением корреляционных факторов в точке Т = Гмь причем антипараллельная корреляция в нематической фазе несколько сильнее, чем в смекти — ческой.
 19 января, 2013
19 января, 2013  admin
admin 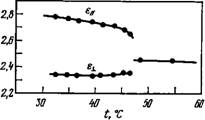
 Опубликовано в рубрике
Опубликовано в рубрике 