The potential value of the application of molecular orbital methods in colour chemistry is immense. In essence, the reason for this is that the methods enable, in principle, many of the light absorption properties of dyes, from a knowledge of their chemical structure, to be calculated with the aid of a computer. Thus, the colour properties of any dye whose structure may be drawn on paper may be predicted, with some expectation of accuracy, without the need to resort to devising a method for the synthesis of the dye in the laboratory. The value to the research chemist whose aim is the synthesis of new dyes with specific properties, perhaps for new applications, is obvious. The properties of a very large number of structures may be predicted in a short period of time using computational methods, and specific compounds for which interesting properties are predicted may be selected for synthesis and an evaluation of application performance. The advances in computer technology, both in terms of software and hardware, which have taken place in recent years and which appear set to continue into the future are certain to mean that the more sophisticated molecular orbital methods will become more and more accessible as a routine tool for the colour chemist. The concepts and mathematical basis of molecular theory are well documented, and this particular text makes little attempt to address the detail of these. The section which follows provides an outline of the basis of the molecular orbital approach to bonding, presenting an overview of the methods which are of particular value to the colour chemist at the present time, and the aspects of colour properties which the methods can address.
In molecular orbital theory, electrons are considered as a form of electromagnetic radiation, i. e. in terms of their wave nature rather than their particulate nature. A principle of fundamental importance to the theory is the quantum principle, which states that the electron can only exist in a fixed series of discrete energy states. An essential concept in quantum theory of relevance to colour chemistry is that electrons are contained in regions of high probability referred to as orbitals. The mathematics underlying molecular orbital theory was first formulated in 1925 by Schrodinger, the solution of whose equation gives a fixed number of values of E which are the energy states available to the electrons in a particular atom or molecule. Unfortunately because of the complexity of the mathematics, even with the computing power currently available, the equation may be solved exactly only for relatively simple atomic and molecular systems. However, a range of approximations may be made to obtain solutions to the equation. Coloured molecules have large molecular frameworks so that approximate methods for solution of the equation to give the required values of E (the energies of molecular orbitals) become even more essential. The simplest of these rely on a range of empirically or semi-empirically derived parameters
Molecular orbitals are considered to be generated by overlap of atomic orbitals. There are two types of overlap. Direct or ‘end-on’ overlap gives rise to a-orbitals, either bonding types, the low energy orbitals which in the ground state of a molecule are occupied by two electrons, or the high energy antibonding (a*) orbitals which remain unoccupied, while re-molecular orbitals are obtained by indirect or ‘sideways’ overlap, for
example from overlap of two singly occupied 2pz atomic orbitals.
Dyes are usually organic molecules with extended conjugation, containing a framework of а-bonds and an associated re-system. The lowest energy electronic transitions occur when an electron is promoted from an occupied re-orbital to an unoccupied re* orbital. It is these re-re* transitions (rather than а-а* which are of much higher energy) that give rise to the absorption of organic dyes and pigments in the UV and visible regions of the spectrum.
The Hiickel molecular orbital (HMO) method is one of the earliest and simplest molecular orbital methods and has proved to be a particularly appropriate method for calculations on conjugated molecules. In the HMO method, it is assumed that the molecular orbitals of a particular structure may be expressed as a linear combination (or sum) of the atomic orbitals present in the molecular system (the LCAO approximation). Essentially this represents a mathematical expression of the assumption that molecular orbitals are derived from overlap of atomic orbitals. The HMO method also assumes that in conjugated systems only the reelectrons are involved in the electronic transitions which take place when light is absorbed and that these transitions are unaffected by the framework of а-bonds in the molecule (the а-re separation principle). This would at first sight appear to be a reasonable first approximation as in conjugated molecules it is generally assumed that the low energy re-re* transitions are principally responsible for UV and visible light absorption.
By calculating the energies of each molecular orbital, the HMO method may be used to provide electronic transition energies for the promotion of an electron from an occupied molecular orbital to a higher energy unoccupied orbital. These energies are obtained in terms of fi, the bond resonance integral, which is treated as an empirical parameter and given a value by comparison of the calculated values with the experimental values obtained from UV/visible spectra. Two other sets of molecular parameters which may be calculated using the HMO method are the re-electron charge densities, Q, the measure of the re-electron charge localisation on each atom in the molecule, and the re-bond orders (P), the measure of the degree of re-overlap of atomic orbitals between each pair of atoms in the molecule. While the HMO method is simple and useful qualitatively, quantitative correlation with spectral data is only reasonable in a few special cases. The method has been shown to give a good correlation between experimental and calculated electronic transition energies with a series of aromatic hydrocarbons, and also with the set of linear polyenes, in the latter case provided that different bond fi-values are used for the formal single and double bonds. In general, while the method appears to give reasonable predictions for hydrocarbons, it works much less well with molecules containing heteroatoms, such as O and N, and this severely restricts its usefulness as a tool for calculating the colour of dye molecules.
The molecular orbital method which has been most extensively and successfully applied to the calculation of the colour properties of dye molecules is the Pariser-Pople-Parr (PPP) approach. Like the HMO method, the PPP-MO method uses as its basic mathematical premise the LCAO approximation in combining atomic orbitals to form molecular orbitals. In addition, it retains the a-% separation principle, essentially neglecting the influence of ^-electrons on the colour. The main way in which the PPP-MO method provides a refinement over the HMO method is by taking account of interelectronic interaction energies, and, in doing so, specifically includes molecular geometry, both of these features being ignored by the HMO method. The theoretical basis of the PPP-MO method is not discussed here, but an outline of the way in which a calculation of this type may be carried out follows.
The sequence of operations involved in a PPP-MO calculation is illustrated in the flow diagram shown in Figure 2.13. The method is illustrated for the case of 4-aminoazobenzene, 15c. The first step involves devising a numbering system for all of the atoms that contribute to the я-system of the molecule. Secondly the total number of я-electrons in the
|
Figure 2.13 The sequence of stages in a PPP-MO calculation for compound 15c, for which an appropriate atomic numbering system is given |
molecule is indicated. In this case, there are 15 relevant atoms and 16 re-electrons, each atom contributing a single electron except for the amino nitrogen atom which donates its lone pair to the re-system. The molecular geometry is then specified in terms of all the interatomic distances and bond angles. Energy parameters, specifically valence state ionisation potentials (VSIP) and electron affinities (Ea), are assigned to all of the relevant atoms and bond resonance integrals values (fi) are assigned to every pair of bonded atoms. The VSIP, Ea and fi-values are treated as a set of semi-empirical parameters which are available from various literature sources and which are commonly modified to suit a particular type of molecule. Finally, to enable the calculations to be carried out the re-electron charge densities (Q) for all relevant atoms and the re-bond orders (P) for all bonded atoms are required. This feature of the PPP-MO method presents the problem that the values for Q and P for specific molecules are not known initially, but they may be obtained after the calculations have been carried out. The solution to this ‘chicken and egg’ problem is achieved by carrying out a preliminary HMO calculation, which gives an approximate set of Q and P values. These values may in turn be used to set up and carry out the PPP-MO calculation and as a result a new, improved set of values is obtained. The process is then repeated until two successive calculations give a consistent result. This iterative process is referred to as a self-consistent field (SCF) method. The procedure leads to a set of molecular orbital energies from which, in principle, electronic transition energies may be calculated. However, since the PPP-MO method uses a set of data based on the ground state structure of the molecule, it predicts ground state energies rather better than excited state energies. To correct for the fact that molecular orbital energies may change after excitation by promotion of an electron from a lower energy occupied molecular orbital to a higher energy unoccupied molecular orbital, and hence to give improved excited state data, a procedure known as configuration interaction (C. I.) is carried out as the last stage of the calculation.
The PPP-MO method is suitable for the treatment of large molecules, does not present major computing demands and programs are now routinely used as a tool to calculate the colour properties of dyes. Unlike the HMO method, it handles heteroatomic species well. The method has been remarkably successful in calculating lmax values for a wide range of dyes from virtually all of the chemical classes. For example, the method provides a reasonably accurate account of substituent effects in the range of aminoazobenzene dyes, including compounds 15a-f and 16a-f which have been discussed in terms of the valence-bond approach in the previous section of this chapter.
|
Table 2.4 Experimental and PPP-MO calculated electronic spectral data for azobenzene and the isomeric amino derivatives
|
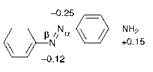
Table 2.4 shows a comparison of the experimental and PPP-MO calculated electronic spectral data for azobenzene and the three isomeric monoamino derivatives. It is noteworthy that the ortho isomer is observed to be most bathochromic, while the para isomer is least bathoch — romic. From a consideration of the principles of the application of the valence-bond approach to colour described in the previous section, it might have been expected that the ortho and para isomers would be most bathochromic with the meta isomer least bathochromic. In contrast, the data contained in Table 2.4 demonstrate that the PPP-MO method is capable of correctly accounting for the relative bathochromicities of the amino isomers. It is clear, at least in this case, that the valence-bond method is inferior to the molecular orbital approach. An explanation for the failure of the valence-bond method to predict the order of bathoch — romicities of the o-, m- and p-aminoazobenzenes emerges from a consideration of the changes in n-electron charge densities on excitation calculated by the PPP-MO method, as illustrated in Figure 2.14.
The valence-bond representation of the ground and first excited states of dye 15c, illustrated in Figure 2.8, would suggest that a decrease in charge density on the amino nitrogen atom and an increase in charge density on the ^-nitrogen of the azo group would be observed on excitation. The changes in charge densities calculated by the PPP-MO (Figure 2.14) indeed predict these effects, but suggest that there is also a significant increase in the charge density of the a-nitrogen atom of the azo
|
Figure 2.14 Some n-electron charge density differences between the ground and first excited states calculated by the PPP-MO method for 4-aminoazobenzene, 15c. |
group, an effect which may not be accounted for using the valence-bond approach. The results demonstrate that the valence-bond assumptions, particularly concerning the structure of the first excited state, are not wholly accurate and as a result it is perhaps not surprising that erroneous predictions are sometimes made.
Because molecular orbital methods such as the PPP approach are capable of calculating л-electron charge densities both in the electronic ground states and excited states of dye molecules, they are particularly helpful in providing information on the nature of the electronic excitation process, by identifying the donor and acceptor groups and quantifying the extent of the electron transfer. One use of this is that it allows the dipole moments of the ground and first excited state to be calculated, and this may be used to account for the influence of the nature of the solvent on the Ятах value of a dye, an effect referred to as solvatochromism. For example, if the dipole moment of a dye molecule is larger in the first excited state than in the ground state, then the effect of a more polar solvent will be to stabilise the first excited state more than the ground state. The consequence will be a bathochromic shift of the absorption maximum as the solvent polarity is increased, an effect known as positive solvatochromism. The reverse effect in which increasing solvent polarity causes a hypsochromic shift is perhaps not surprisingly referred to as negative solvatochromism.
The PPP-MO method is capable of calculating not only the magnitude of the dipole moment change on excitation, but it can also predict the direction of the electron transfer. The vector quantity that expresses the magnitude and direction of the electronic transition is referred to as the transition dipole moment. For example, the direction of the transition dipole moment of azo dye 15f as calculated by the PPP-MO method is illustrated in Figure 2.15.
The direction of the transition moment is of practical consequence in dyes used in liquid crystal display systems. It is important for such applications that the direction of the transition moment is aligned with the molecular axis of the dye. Since this is the case with azo dye 15f, the dye would appear to be a reasonable candidate as a liquid crystal display dye (see Chapter 10 for further discussion of this application of dyes).
The intensity of colour of a dye is dependent on the probability of the electronic transition. A familiar example of this principle is provided by
|
Figure 2.15 Direction of the transition moment in azo dye 15f. |
the colours due to transition metal ions in solution which are normally weak because the d-d transitions involved are ‘forbidden’, i. e. of low probability. In contrast the n-n* transitions due to organic dyes, which involve considerable charge transfer in donor-acceptor chromogens, are highly probable and thus give rise to much more intense colours. While most of the research published on the application of molecular orbital methods, such as the PPP approach, centres on their application to the calculation of lmax values, the ability to predict the tinctorial strength of a dye is arguably of greater practical value since it is directly related to the economic viability of the dye. If, for example a new dye has twice the colour strength of an existing dye, then the dyer need only use half the quantity of that dye to obtain a given colour. Provided that the new dye costs less than double that of the existing dye, it will therefore be more cost effective. The PPP-MO method is capable of providing a quantitative account of colour strength by calculating a quantity,/osc, known as the oscillator strength. This parameter is given by the following equation:
fosc = 4.703 x 1029 x M2 / 2M
where M is the transition dipole moment and XM is the mean wavelength of the absorption band. As the data given in Table 2.4 demonstrate, there is a reasonable correlation in qualitative terms between the calculated oscillator strengths and the experimental molar extinction coefficients, e, for the series of azo dyes in question. In general, a reasonable correlation between fosc and e for broad classes of dyes may be achieved, although within specific classes the correlation is less good. This may well be due to the fact that PPP parameterisation has been optimised for correlation with 2max values rather than molar extinction coefficients. It may be argued that the oscillator strength gives a better measure of colour intensity than the molar extinction coefficient (e) as it expresses the area under the absorption curve, whereas e is profoundly dependent on the shape of the curve. It is only valid to relate the e values to the intensity of colour for a series of dyes if the curves are of similar shape.
Brightness of colour is expressed by the width of the visible absorption band. This bandwidth is determined by the distribution of vibrational energy levels superimposed on the electronic ground and excited state energy levels. Broadening of the absorption bands may be caused in a number of ways. For example, an increase in the number and spread of energies of bond vibrations will generally lead to broader absorption bands. This argument may be used to provide an explanation as to why the relatively simple structure of heterocyclic azo dyes such as compound 18 and 19 give brighter blue colours than the multi-substituted carbocyc — lic analogues such as compound 17 with its increased number of vibrational levels. Some of the brightest colours are provided by the phthalocyanine chemical class (see Chapter 5). The colour of these dyes and pigments owe their brightness in part to their rigid molecular structure both in the ground and excited states, both states showing similar geometry and little vibrational fine structure. Because it is related to the vibrational characteristics of the molecules rather than their electronic structure, it is at first sight difficult to envisage how the PPP-MO might be useful in calculating bandwidths. A solution to this problem has been provided by the application of an empirical extension of the PPP-MO method to the calculation of the Stokes’ shifts of fluorescent molecules. Using the assumption that there is a simple relationship between absorption bandwidths and Stokes’ shifts, both parameters being dependent on vibrational energy levels in the two electronic states, the method has been adapted, with some success, to the calculation of bandwidths.
The PPP-MO method has proved extremely successful for the prediction of a wide range of colour properties, and it is currently the most extensively used method for this purpose. It does have some deficiencies. For example, the method carries out its calculations based on ^-electrons only and therefore cannot, except in a rather empirical way, account for some of the subtle effects of а-electrons on colour. Among such effects commonly encountered are hydrogen bonding and steric hindrance. As more and more powerful computing facilities become accessible, there is clear evidence that colour chemists are turning their attention towards the use for colour prediction of more sophisticated molecular orbital techniques which take into account all valence electrons, such as the CNDO and ZINDO approaches, and in due course they may well prove to be the methods of choice. However, at the present time, it has not been established with absolute certainty that these methods will routinely provide superior colour prediction properties.
 3 сентября, 2015
3 сентября, 2015  Pokraskin
Pokraskin 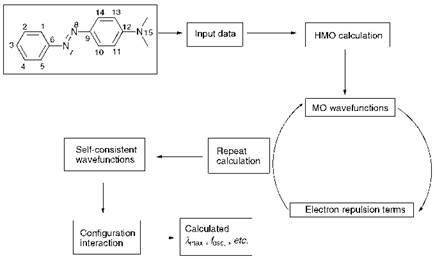

 Опубликовано в рубрике
Опубликовано в рубрике 