The adhesion of the rubber spheres is revealed unequivocally by their leaping into contact. However, the precise nature of this contact needs to be understood if the adhesion of the spheres is to be well defined. Consider the two rubber surfaces magnified so the contact region in the equilibrium contact shows up more clearly, as in Fig. 3.13(a).
The rubber, after jumping into contact, has spread to form a flat circular contact spot about one millimeter in diameter. This flattening is a general mechanism of adhesion, similar to the spreading of the liquid droplet described previously in Fig. 3.10. However, the rubber cannot spread far because it is elastic and not liquid like the droplet. The flattening and spreading of the rubber causes an elastic resistance to build up in the rubber, storing energy, much as an elastic band does when stretched. This stored energy can be seen in the change in shape near the contact, from spherical to neck-like. Eventually, this elastic resistance
|
Figure 3.13. (a) Magnified contact region between two equal rubber spheres in equilibrium, (b) Applying a tension force causes the neck to extend and eventually break, illustrating the cracking mechanism. |
stops the spreading and the equilibrium contact is attained. The size of the contact spot at this stage is a measure of the molecular adhesion. A large spot is a measure of large adhesion.
This spreading and equilibrium is an example of the third law of adhesion. The molecules jump into contact with a particular energy, but that energy has to be absorbed into the system by a mechanism which can be quantified. This mechanism is hugely important because it affects the forces of adhesion enormously. For example, if the rubber is not perfectly elastic when flattened, then the contact spot size is different. The same molecules can be in contact, yet a slight change in the mechanism can raise or lower macroscopic adhesion by orders of magnitude, as we will see later in Chapters 7 and 8.
In Fig. 3.13, the mechanism for separation of the particles is seen to be elastic cracking. The neck-like shape is precisely what would be expected of a crack. This can be shown by applying a tensile force as in Fig. 3.13(b). As the force is applied, the neck extends, the crack opens, and the contact spot shrinks as the crack penetrates the interface. If the tension force is small, then the contact will not break completely, but reaches a new equilibrium position, at a smaller contact size. This is an equilibrium crack of the kind first described by Griffith in 1920.13 He showed that such cracks can be described by an energy balance theory, in which the surface energy of the crack is held apart by the elastic energy in the rubber, plus the potential energy of the tensile force. This theory is a concept of pure mechanics which does not require any molecular interpretation, but is expressed in mathematical terms as a continuum theory. So we conclude that the molecules jump into contact, but they are impeded by the crack mechanism, which can be explained by fracture mechanics. Thus we follow the argument from molecules, through mechanism, to mechanics.
|
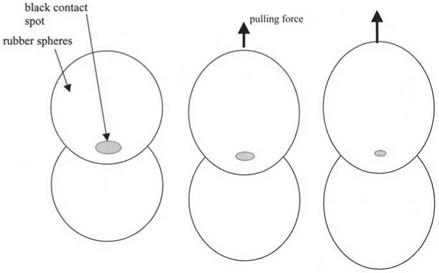
Figure 3.14. Two rubber spheres in a molecular contact over the black contact spot region, then pulled apart by force, causing the crack to run through the contact. |
As a larger and larger tensile force is applied to pull the rubber spheres apart, the contact gets smaller and smaller in diameter. However, the contact spot does not shrink gradually down to zero. Instead, a point of instability is reached where the crack speeds up suddenly and the spheres rapidly come apart. This is shown diagrammatically in Fig. 3.14.
The crack can be in equilibrium over a certain range of forces, but above a particular tension, i. e. the pull-off force, the spheres catastrophically jump apart as the crack moves suddenly through the contact spot. This pull-off force is another measure of the molecular adhesion between the spheres. A large force indicates large adhesion.
 10 сентября, 2015
10 сентября, 2015  Pokraskin
Pokraskin 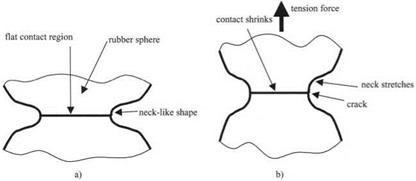
 Опубликовано в рубрике
Опубликовано в рубрике 