Clearly the adhesive must wet the adherend, implying the common- sense idea of a thin film of liquid spreading uniformly without breaking into droplets on the surface (Fig. 3.3). The water break — free test is the simplest approach to a qualitative visual assessment; the thermodynamic approach to wetting allows quantitative study.
Surface tension is a direct measurement of intermolecular forces. At the surface of a liquid, there is an imbalance of attractive forces between neighbouring molecules, so that work has to be done on molecules to bring them to the surface. Surface molecules thus possess a higher energy than those within the bulk liquid and this extra energy is termed the ‘surface free energy’ or ‘surface energy’. Surface energy and surface tension are dimensionally equivalent and numerically the same, and are represented by y. Surface energy
|
|
may generally be expressed by two terms, namely a dispersion, yD, and a polar, yp, component, which may be determined experimentally, such that
у = yD + yp
Fig. 3.4 illustrates the surface tension vectors at the three-phase point of contact of solid, liquid and vapour. The Young equation relating these tensions to 0 is
7sv = 7sl + 7lv cos 0
ySv represents the surface free energy of the solid substrate resulting from adsorption of vapour from the liquid, and will be lower than the surface free energy of the clean bare solid surface in vacuo, ys. Dupre considered the work needed to separate a layer of liquid from a solid surface, viz
![]() (energy of new) (energy of)
(energy of new) (energy of)
(surfaces created) (interface destroyed)
This is the work of adhesion, WA, and is given by = 7s T 7lv — 7sl
The difference between ys and ysv is known as the spreading pressure, tts, of the liquid’s vapour on the solid surface. These two classic equations may then be combined so that
= yLv (1 — cos 0) + tts
Intuitively, optimum performance is expected if the liquid adhesive exhibits a zero or near zero contact angle, 0, giving a high value of
Real solid surfaces are not flat, so that observed contact angles
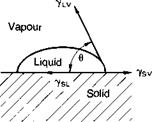 -yLV = surface free energy of liquid
-yLV = surface free energy of liquid
-ySL = surface free energy of solid/liquid interface
-ysv = surface free energy of solid/vapour interface
6 = equilibrium contact angle
Fig. 3.4. Liquid drop resting at equilibrium on a solid surface.
would be apparent only, and liquids may spread along fine pores and crevices by capillary action. Maximum wetting will be achieved when the capillary pressures are highest and viscosity is lowest, but surface micro-topography will introduce further complications^,11, 16). The mixture of materials comprising most structural adhesives will influence wetting in a complex fashion. Selective adsorption of one component may provide dramatic changes in wetting rates or phase separation may occur, and both may be deliberately inbuilt into the adhesive formulation by the manufacturer to achieve a desirable balance of properties. Attempts to measure the contact angle of a drop of practical adhesive on a real surface are therefore fraught with considerable problems of experimental control and in subsequent interpretation. Surface wetting is, in fact, a kinetic phenomenon so that even if the ultimate equilibrium contact angle is zero, the advancing contact angle is never zero, but is a function of the rate of movement of the liquid and increases with increasing velocity(7,ll). Hewlett and Pollard(17) devised a method for studying the dynamic contact angles of epoxies with regard to the repair of concrete with low viscosity injection resins. Unfortunately, they were unable to judge the various merits of the silane adhesion promoters incorporated in the resins.
Wetting involves a reduction in interfacial energy and Huntsberger(9) showed that, other than in exceptional circumstances, the free energy always decreases upon liquid/solid contact. It is concluded that, although most practical adhesives exhibit acute contact angles with their adherends, complete wetting may still occur so that the zero contact angle criterion for wetting (and therefore adhesive selection) is not valid. Bond performance may therefore be assumed to be determined by interfacial energies rather than by surface wetting.
 14 июля, 2015
14 июля, 2015  Malyar
Malyar 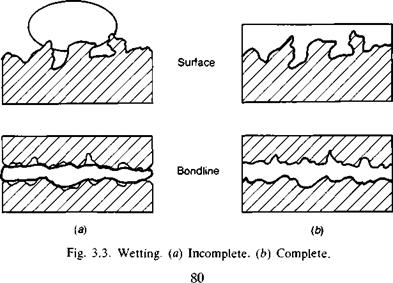
 Опубликовано в рубрике
Опубликовано в рубрике 