Closed form solutions. Structural adhesive joints are generally designed to be loaded in shear so that treatments of joint analyses are confined essentially to the transfer of load by shear, with some consideration of the transverse normal stresses induced by eccentricities in the load path. In the simplest case the adhesive and the adherends are assumed to behave elastically. The most refined analyses attempt to model the situation when the adhesive yields so that the adhesive and, eventually, the adherends behave plastically as the imposed load is raised. Closed-form analyses are difficult to apply to other than simple geometrical configurations, while a major difficulty with the elasto-plastic model is how to characterise the adhesive.
The empirical approach to the design of simple overlap joints was to construct a correlation diagram (Fig. 4.3) between failure load
P = applied load/unit width of joint h = adherend thickness 2a = overlap length
![]()
 Fig. 4.3. Empirical correlation diagram.
Fig. 4.3. Empirical correlation diagram.
and the joint geometrical ratio h/2a, for a particular set of test conditions. Alternatively, if the apparent shear stress at failure of a series of lap joints is plotted against the ‘joint factor’ y/i/2a, as recommended by de Bruyne(13), an approximately straight line is obtained over a wide range of adherend thicknesses (h) and overlap length (2a). This factor works well with adhesives that give ductile failures, but has limited applicability to rigid adhesives. Inspection of the stress concentration coefficient, Д, as derived by Mylonas and de Bruyne(14), indicates the presence of the ‘joint factor’:
where
Ga = shear modulus of adhesive E = Young’s modulus of adherend t = thickness of adhesive
This expression correctly shows that the overlap length should depend upon the modulus of the adhesive.
The mathematical treatment of joint analysis is to set up a series of differential equations to describe the state of stress and strain in a joint. By using stress functions or other methods, closed-form algebraic solutions may be obtained. In the simplest elastic case it should be possible to devise a solution for given boundary conditions. As non-linearities arise, such as joint rotation and material plasticity, various assumptions need to be made to give solutions. However, once obtained, these solutions may be used to great advantage in a parametric study, provided the limits of the simplifications are borne in mind. The classical early work of Volkersen(15) and of
Goland and Reissner(16) was limited because the peel and shear stresses were assumed constant across the adhesive thickness, the shear was assumed a maximum at the overlap end (and not zero as it must be at a free surface), and the shear deformation of the adherends was neglected. Later, several analysts including Renton and Vinson(17) and Allman(18) produced solutions where the adherends were modelled to account for bending, shear and normal stresses. Adhesive shear stress was set to zero at the overlap ends. Allman additionally allowed for a linear variation of the peel stress across the adhesive thickness, although his adhesive shear stress was constant.
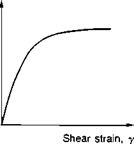
Later, extensive studies were carried out by Hart-Smith(19) during the Primary Adhesively Bonded Structure Technology (PABST) programme, which ran from 1976 to 1981, to account for adhesive elasto-plastic behaviour. He developed many computer programs for analysing various joint configurations, requiring the input of an idealised adhesive stress-strain curve (Fig. 4.4(a)). Similar programs are available from the Engineering Sciences Data Unit (ESDU) in London for elastic(20) and inelastic(21) calculations, developed from the work of Volkersen and Goland and Reissner. In Hart-Smith’s work, yield stress was effectively equated to the failure stress so that failure occurs when the adhesive reaches its limiting shear strain. By increasing the overlap length, the lightly stressed region in the middle of the joint is enlarged. Current aerospace design philosophy views this as essential to offset the effects of creep at the ends of joints if low cycle creep/fatigue loading is encountered
 |
 |
Shear stress, t
(a) (b)
Fig. 4.4. Design of bonded lap joint (Ref. 19). (a) Idealised adhesive shear stress/strain curve. (b) Design of bonded double-lap joints.
(e. g. the pressurisation/de-pressurisation cycles encounted by aircraft fuselages). Fig. 4.4(h) summarises Hart-Smith’s design criteria for double-lap joints. The overlap is designed for the worst service condition, which is usually when the adhesive has been softened by moisture and elevated temperature. The plastic zones are calculated to be long enough to carry the ultimate load, the central elastic region large enough to prevent creep, and the minimum operating stress must not exceed 10% of the adhesive shear strength. In the PABST programme a ratio of overlap length to adherend thickness of 80 : 1 was chosen for single-lap joints. Armstrong(22) reports that Boeing used 50 : 1, but that Douglas prefer a ratio of 80 : 1. It should be borne in mind that these design philosophies were developed specifically for aircraft construction involving the bonding of thin metal alloys. Whilst representing a significant advance in the design of structural adhesive lap joints, they may not be generally applicable to other engineering applications.
Pera International, in collaboration with France’s Centre Technique des Industries Mecaniques (CETIM), developed an approach to the prediction of bonded joint strength during a four-year (1986-90) project called Adhesive Bonding Technology for Engineering Applications (ADENG) funded through the European Community’s BRITE/EURAM programme. The approach, whilst based upon the use of software employing closed-form analyses, represents a very useful design tool of general applicability to bonded joints encountered commonly in production engineering. Other useful software design techniques under the names of BISEPS-TUG (Bonded Inelastic Strength Prediction Suite — Tubular Geometry) and — LOCO (Lap Joint Combined Loading) have been developed by the Materials Development and Engineering Divisions of Harwell Laboratory, also largely within European Community-funded programmes during the 1980s. CADEPT, an expert system for the design of adhesively bonded coaxial joints, has also been developed more recently by the Harwell Laboratory. Some rudimentary analytical capability also forms part of Permabond Adhesives’ Locator (PAL) software.
The methods developed over the last decade or so to predict failure employ in-bondline non-linear adhesive characterisation. This in turn requires some fairly sophisticated experimental techniques, carefully conducted for a range of test conditions and environments. Hart-Smith concluded that a precise representation of the adhesive stress-strain characteristic is not important. He maintains that the adhesive failure criterion, in shear, is defined uniquely by the adhesive shear strain energy per unit bond area, regardless of the individual characteristics which contribute to that strain energy.
Finite element analysis. The finite element method is now a well — established technique for modelling mathematically stress analysis problems. Its great advantage lies in the fact that the stresses in a body of complex geometrical shape under load can be determined. The method is therefore well suited for analysing and optimising adhesive joint geometries, particularly when formed with adhesive spew fillets at their extremities. The method also avoids the approximations of the closed-form theories, thus enabling more accurate answers to be found. However, because of stress gradients both across and along the adhesive layer, it is necessary to use quite a large number of elements to give sufficient resolution even in standard model lap joints.
Adams and co-workers have been amongst the main proponents of this method in its application to a realistic analysis of bonded lap joints(5). Harris and Adams(23) presented a non-linear analysis that was able to take account of large displacement joint rotations and elasto-plastic properties of both adhesives and adherends. It was used to predict the mode of failure and ultimate load of single lap joints constructed with aluminium adherends and epoxy adhesives. The results were compared with those obtained from experiment and closed-form analyses. They found that a failure criterion based on the triaxial tensile properties of the adhesive (which they then approximated to the uniaxial tensile properties) could be assigned to these particular joints. For the untoughened adhesives a maximum stress criterion was appropriate, while for the toughened adhesives a maximum strain criterion could be employed. Again, fairly sophisticated adhesive characterisation was required, both for the analysis and for the assignment of the failure criteria. Further development of Harwell’s BISEPS software has added some finite element capability to their suite of closed-form programs.
For investigations into real joints the finite element technique is very powerful. The trouble is that each solution applies only to a given set of parameters so that many computer runs are required for a parametric analysis. Even with mesh generation programs, the cost in mainframe computing time can be rather high if it is necessary to model the structure with a large number of elements; however, the advent of powerful PCs may soon render rapid and economic analysis practicable.
The fracture mechanics approach. Traditional structural design in conventional materials compares average strain, and therefore average stress, distributions acting on some ultimate criteria. For designs involving brittle flaw-sensitive materials such procedures are less satisfactory. Adhesive joints usually fail by the initiation and propagation of flaws and, since the basic tenet of continuum fracture mechanics is that the strength of most real solids is governed by the presence of flaws (Griffith(24)), these theories have proved to be extremely useful in their application to adhesive joints. Comprehensive review material related to adhesive joints is given by Kinloch(4), Anderson et al.(25), Bascom et al.(26, 27) Kinloch and Shaw(28), and Ripling et al.(29). Basically, two inter-relatable conditions for fracture have been proposed.
First, the energy criterion for fracture, which is simply an extension of Griffith’s hypothesis. He postulated that fracture occurs when sufficient strain energy is released to satisfy the requirements of the new surface area created at the instant of crack propagation. In fact, crack initiation involves a number of energy consuming processes within the immediate vicinity of the crack tip so that the Griffith equation requires some modification, as proposed by Irwin(30). This approach therefore provides a measure of the energy required to extend a crack over unit area and is termed the fracture energy or strain-energy release rate, Gc.
Second, Irwin found that the stress field surrounding a crack could be defined uniquely by a stress-field parameter termed the stress-intensity factor, K. He postulated that fracture occurs when the value of К exceeds some critical value, Kc, often referred to as the material fracture toughness. Thus К relates the magnitude of the stress-intensity local to the crack in terms of the applied loadings and the geometry of the structure in which the crack is located. A crack in a solid may be stressed in three different modes as depicted in Fig. 2.18. Mode I opening, and hence the Mode I value for the stress intensity factor Kt, is the most critical situation in bonded joints.
Hence the condition
Kt > Klc (4.2)
represents a fracture criterion. It may be related to the geometry of any particular structure via the equation
Klc = Qac{Ttat? (4.3)
where Q is the configuration correction factor as a function of geometry and loading, crc is the stress at crack initiation, and af is the flaw size.
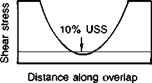
Pure Mode I fracture energy is known to be considerably less than either of the other modes, but many practical situations involve combined-mode loading about which little is known(31). Bascom and Hunston(27) demonstrated that the use of Mode I fracture energies in design was not conservative because of mixed-mode effects, especially where elastomer-modified adhesives are to be employed. Various test procedures have been devised to obtain values for Gic and KiC for an adhesive, from both bulk and joint specimens. Like other material properties these are not unique values, but rather are dependent upon the rate and temperature of testing, environmental conditions, and the geometry of the specimen. Constraining the adhesive as a thin bondline between high modulus substrates may also complicate the problem because of its influence on the development of the plastic zone (Fig. 4.5). Further, Bascom et al.(26) suggests that the size of this zone is very much larger than that associated with untoughened adhesives.
The relationships between G and К for a crack in a homogeneous material are given by:
|
K = EG |
for plane-stress |
(4.4) |
|
ip — EG 1 (1 — v2) |
for plane-strain |
(4.5) |
For a crack in an adhesive layer these relationships are still generally valid so that К (joint) and G (joint) may be correlated through E (adhesive), albeit approximately in the case of very thin adhesive layers. For a crack near an interface though, the interpretation of К is more complex, probably involving values for and Кц.
A major advantage of the fracture mechanics approach to joint failure is that it is applicable equally to cohesive and adhesive failure
|
zone Fig. 4.5. Change in crack tip deformation zone with increasing bondline thickness (Ref. 27). |
modes. The significance of this advantage in elucidating the mechanics and mechanisms involved in joint failure will be apparent. Indeed, the success of this approach is demonstrated by the widespread adoption of test methods based upon fracture mechanics principles in the aerospace industry.
The significance of the fracture mechanics approach to joint design is that Gc or Kc may be related to a critical crack length in the structure. Cracks which are shorter are safe, and cracks which are longer are self-propagating and potentially catastrophic. Thus structures may be designed to accommodate cracks of a predetermined length without breaking. This length naturally has to be related to the size of the structure and also to the probable service and inspection conditions. The fail-safe design concept, according to Parker(31), assumes that in spite of the failure (or incipient failure) of an individual component, the complete structure is safe from overall catastrophic failure. Practically, such designs may be achieved by (a) multiple load paths encouraged by stringers (b) crack arrestors to inhibit propagation (c) routine inspection. In bonded joints the use of toughened adhesives to inhibit crack propagation is an attractive solution, so long as fracture is energetically favoured within the adhesive layer, and provided that other performance aspects are not compromised unduly by the toughening.
 27 июля, 2015
27 июля, 2015  Malyar
Malyar 
 Опубликовано в рубрике
Опубликовано в рубрике 