Лако-красочные материалы — производство

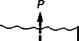
Despite the fact that adhesive joints are rarely designed to be loaded directly in tensile mode, tensile tests are common for ‘evaluating’ adhesives. The axially-loaded butt (or ‘poker chip’) joint geometry, as recommended by ASTM D897(52), is depicted in Fig. 4.11.

A close look at the stress state induced within this joint indicates clearly a complex interaction of strain, and there are many useful commentaries on the limitations of this test(4, 5, 25, 31). If the adherend and adhesive moduli are very different (e. g. the ratio of epoxy to steel moduli, EIEa = 40), the axial strains in the adhesive will be about 40 times greater than those in the adherend with a similar ratio for the lateral (Poisson’s) strains. Where the two materials join, this conflict is resolved by generating large interfacial radial shear stresses (Fig. 4.11(c)). Joint strength increases with a decrease in adhesive thickness, and in a thin bondline affected completely by adherend restraint a complex stress arises. The ratio of the applied stress to the strain across the adhesive is then defined as the apparent or constrained Young’s modulus, E’a(5).

(a) (b)

Fig. 4.11. Tensile (cylindrical) butt-joint test, (a) Unloaded. (b) Loaded, (c) Stress distribution.

If purely elastic behaviour is considered, elastic response of the adhesive may be obtained by attaching extensometers to the adherend either side of the bondline, making a suitable correction for adherend strain. Beyond the elastic limit, yield of the adhesive may be suppressed by the triaxial stress state, occurring at a stress higher than that in uniaxial tension. On the other hand, brittle adhesives which fracture before they yield will probably indicate a low failing stress because of stress concentrations.

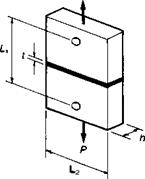
One attempt to minimise the generation of large interfacial radial shear strains is reported by Renton(32), and advised by ESDU 81022(43). The geometry of the butt-joint is shown in Fig. 4.12 and it is implicit that the bondline thickness must be kept

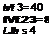
Recommended geometrical ratios:

e. g. f = 0.15 mm h = 8 mm L2 = 28mm t, = 250 mm

Fig. 4.12. Tensile butt-joint (Ref. 32). 148

to a minimum if the overall specimen dimensions are to be kept within reasonable proportions. Renton states that this geometry gives a relatively uniform distribution of normal and shear stress over a large area, so that adhesive response may be determined from bondline deformation measurements. However, in the American evaluation programme this geometry was found to be very sensitive to temperature, moisture and strain rate. Moreover, deformation measurement was severely influenced by deformation of the aluminium adherends, and by included bondline air voids; a 10% void volume resulted in a 39% change in bulk modulus. For bondline thicknesses in excess of 0.6 mm, the specimen dimensions would clearly become very large.

It would seem that tensile stress-strain data determined from the butt-joint would be rather difficult to use to predict the failure of other than similar joints.