Лако-красочные материалы — производство

To gain insight into the adhesive-surface interaction on a molecular level, and thus compare the effectiveness ofdifferent surface preparation procedures, contact angle measurements have frequently been discussed. Prediction of the adhesive properties of a surface based on its interfacial tension can be possible because adhesion will only take place if the adhesive wets the adherent surface as completely as possible (see Chapter 3).

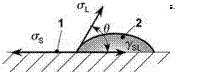
The shape of a liquid drop (e. g. a liquid adhesive) placed on a solid surface depends on the interfacial surface-liquid interaction. In the case of complete wetting, the liquid spreads on the surface (contact angle 0 = 0°). If the wetting is incomplete, then a finite contact angle is established and a three-phase contact area appears. At this point, three phases arc in contact: the solid; the liquid; and the vapor (Figure 6.16). Here, Young’s equation relates the contact angle to the interfacial

tensions gsl. Gl and aS:

Gl ■ cos0 = Gs — gsl (6.1)

If the interfacial tension of the bare solid surface gs is higher than that of the solid-liquid interface gSL, then the right-hand side of Young’s equation is positive. Then, cos 0 must be positive, the contact angle is less than 90°, and the liquid partially wets the solid. If the solid-liquid interface is energetically less favorable than the bare solid surface, the contact angle will exceed 90°, allowing cos 0 to be negative. If the contact angle is greater than 90°, the liquid is said not to wet the solid.

The Dupre-Young equation relates the work of adhesion to the interfacial tensions:

Wad = Gs + Gl gsl (6.2)

By introducing Young’s equation into Dupre’s equation, the Young-Dupre equation is obtained:

Wad = Gl (1 + cos 0)l (6.3)

Depending on the surface chemistry, the interfacial tension in the liquid-solid contact can be influenced by polar and nonpolar (dispersive) interaction. According to Owens, Wendt, Rabel and Kaelble, the interfacial tension gSL can be calculated by subtracting the polar and dispersive share of the interfacial tension in the following way:

gSL = GS + GL-2 V gD ■ gD WGp ■ Gp

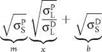After introducing into Young’s Equation and linear regression according to y = mx + b:

As a general rule and precondition for adhesive bonding, the interfacial tension of the bare solid gs, which can be determined by contact angle measurements in the manner described above, must be larger than the surface tension of the liquid adhesive. Typical surface tension values for adhesives range from 35 to 50 mN m-1, depending on the composition. When the surface tension of the surface to be bonded is too low (e. g. in the case of nonpolar polymer materials such as PTFE, PE or PP, or fatty contaminants), it is recommended to perform a suitable surface preparation that

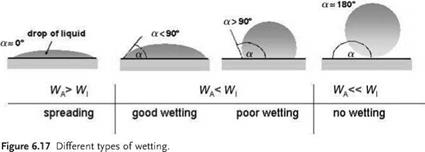increases the surface tension of the adherent surface, or thoroughly removes the contaminants. Figure 6.18 provides an overview of the current surface pretreatment techniques used in bonding technology. In order to obtain good adhesive properties, those surface preparation methods should be chosen which especially enhance the polar share of the substrates surface energy for it to be able to interact with polar groups in the adhesive and thus promote interfacial bonds with a high level of binding energy.

6.2.5