For the design of structural adhesive bonded joints, it is necessary to take the time-, deformation — and temperature-dependent behavior of the adhesive polymeric materials into account.
Modern finite element analysis methods and tools allow a prediction ofthe stress distribution and deformations to be expected in an adhesively bonded joint, provided that the relevant material parameters are available. Only then, is it possible to exploit the full potential of adhesive bonded joints for lightweight construction and for the realization of economically optimized joints. As an example, Figure 6.1 shows the typical dynamic mechanical analysis (DMA) plot of a cold-setting, two-part epoxy
|
Figure 6.1 Typical dynamic mechanical analysis (DMA) plot of a two-part epoxy adhesive. |
102 I 6 Design, Production and Quality Assurance of Adhesive Bonded Joints 60 50
 ^ 40
^ 40
$ 30
ш
0) 20 10 0
resin adhesive, illustrating the decrease of the storage modulus as a material characteristic of the elastic behavior in a temperature range between -50 °C and 150 °C, which is relevant in most applications.
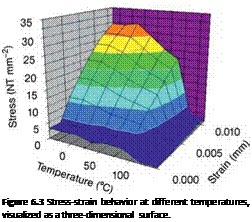 |
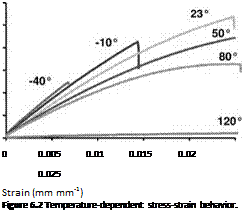
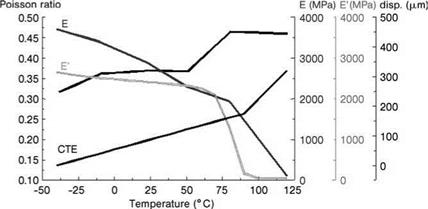
Tensile tests performed on polymer specimens at different temperatures provide an insight into the stress-strain behavior within this temperature range (Figure 6.2). Several single curves add to a three-dimensional surface indicating the stress and strain to be expected as a function of temperature (Figures. 6.2 and 6.3). The further materials data needed are the Poisson’s ratio and the coefficient of thermal expansion, which again both depend on temperature. The course of the storage and loss moduli is illustrated in Figure 6.4. If a bonded joint is intended for long-term exposure in a humid environment, the polymer will usually absorb water, thus modifying its strength and deformation properties which, in turn, may also be influenced by the surface condition of the adherents (see Chapter 3). A precise localized prediction of the stresses in a nonequilibrium state of water uptake is difficult in this case. It is recommended, therefore, to determine all of the above-described material characteristics on dry adhesive specimens and again after conditioning in water until saturation to obtain an indication of the properties range, which needs to be considered.
|
Figure 6.4 Temperature-dependence of the coefficient of thermal expansion (CTE), Poisson’s ratio and modulus of elasticity. |
In order to include the failure behavior in the simulation and to apply a multiaxial failure model, more sophisticated design tools are required. Commonly, the von Mises yield criterion is used for this purpose but, in the case of polymers, this often does not adequately describe the maximum admissible strain in the case of a multiaxial state of stress. The polymer behavior is better described by the Drucker — Prager model, which describes the multiaxial yield stresses by the surface of a cone.
To ensure that the maximum admissible strains and failure mechanisms obtained from simulation properly describe the individual case of application, calibration tests must be performed on standard samples, and the results verified on the components in order to assess whether the data obtained from the finite element analysis, which are based on simplified material parameters and strength hypotheses, are reliable and valid.
6.1.2
 2 октября, 2015
2 октября, 2015  Pokraskin
Pokraskin 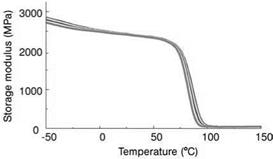
 Опубликовано в рубрике
Опубликовано в рубрике 