Лако-красочные материалы — производство

На основе векторного представления о цвете возникает возможность проведения как операций сложения двух или нескольких цветов, так и операций вычитания. Смешение цветов, сводящееся к их сложению, называется аддитивным смешением.

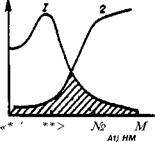
Рис. 1.8. Субтрактивное смешение синего (/) и желтого1 (2) цветов.

Если мы имеем несколько единичных цветов fi, h,-.., fn с координатами Х, Yb Z\Х2, Y, Z2 ХП, Y, Z, то в результате сложения т единиц одного цвета, т2 единиц второго цвета и т. д. получим новый цвет mf

т/-т, Л + тл + … + тл. (1.18)

Легко показать,-что координаты цветности нового цвета, полученного в результате сло­жения нескольких цветов, могут быть выражены следующим образом:

mXi + mX2+ … —тХ„ _ tnY 4-ГП2У2+ … + mY. ,«,

Х~ X+ Y+Z ‘ у X+Y+Z ‘ { ‘

Поскольку модуль суммы векторов равен еумме модулей, можно записать:

m_X+Y+ZXnl—m2 + … +т«. (1.20)

Из этих уравнений следует, что в случае аддитивного смешения двух цветов соотношения координат цветности можно представить сле­дующим уравнением:

У2 — У Х2 — Х

Это выражение представляет собой уравнение прямой, проходящей через две точки с координатами ху и х2у2, т. е. через две точки на цветовом графике, соответствующие двум исходным цветам. Таким обра­зом, цвет, полученный в результате аддитивного смешения двух цветов, обязательно лежит на прямой, которая соединяет точки, соответствую­щие исходным цветам на цветовом графике.

Вычитание цветов — столь же возможная операция, как и сложение. Смешение цветов, сводящееся к их вычитанию, носит название субтрак­тивного смешения. Однако, если операция сложения цветов всегда реально выполнима, то вычитание возможно только в том случае, если имеет место взаимное перекрывание спектров пропускания или отра­жения. Разберем эту операцию на примере субтрактивного смешения желтого и синего цветов. На рис. 1.8 изображены спектры пропускания синего (/) и желтого (2) светофильтров. Белый свет от источника, пройдя через синий светофильтр, будет иметь спектр, соответствующий спектру пропускания этого светофильтра. Правая часть спектра сре­жется, и через желтый светофильтр пройдет только свет, соответствую­щий заштрихованному участку. Этот свет имеет максимум ня спектре, соответствующий длине волны 550 нм. Таким образом, в результате субтрактивного смешения синего и желтого цветов получится зеленый.

Используя явление субтрактивного смешения, получают смешанные зеленые пигменты путем механического смешения или соосаждения желтых и синих пигментов (смеси фталоцианина меди или железной лазури с желтыми кронами). Это же явление лежит в основе много­цветной типографской печати.

Одним из наиболее важных технических свойств пигментов является укрывистость, или кроющая способность. Под укрывистостью понимают пособность пигмента или пигментированного материала делать неви­димой поверхность, на которую наносится лакокрасочный: материал.

По ГОСТам укрывистость выражается количеством (в г) пигмента, юторое необходимо нанести на поверхность в виде однописгментной [асты, чтобы сделать невидимым собственный цвет поверхности пло — цадью 1 м2. В ряде стран укрывистость измеряется в м2/кг, г. е. для Езмерения укрывистости принята величина, показывающая площадь юверхности (в м2), которую можно укрыть, израсходовав 1 кг пигмента или лакокрасочного материала). В ряде случаев такой способ выра — кения укрывистости представляет большие удобства, и в дальнейшем сложении мы будем иногда им пользоваться, нааываяс эту величину фоющей способностью.

Укрывистость, или кроющая способность красочной пленки опреде — [яется отражением и поглощением света, которые, в свою очередь, ЕВЛЯЮТСЯ следствием рассеяния и поглощения света частицами пиг­мента. В случае белых или слабоокрашенных пигментированных пленок ia первый план выступает отражение света материалом покрытия. Укрывистость интенсивно окрашенных и черных покрытий определяется лавным образом поглощением света. Поверхность считается укрытой, ‘ели толщина красочной пленки такова, что отношение коэффициента сражения покрытия над черной подложкой R4 к коэффициенту отра — кения над белой подложкой Re равно 0,98 (/?ч//?б=,98) .

Используя коэффициенты поглощения и рассеяния, Гуревич, Ку — 5елка и Мунк рассмотрели оптические явления, происходящие в пленке (рис. L9). Световой поток /, проходя через слой толщиной dx, ослаб — тяется на величину di. Ослабление за счет поглощения света в слое эавно Ш dx, где К — коэффициент поглощения; ослабление светового потока за счет рассеяния — Sidx, где S — коэффици€Нт рассеяния. Навстречу световому потоку i идет поток у, отраженный от подложки. _, Он тоже будет ослаблен за счет поглощения на величину Kj dx и за > :чет рассеяния на величину Sjdx. Следует отметить, что в теории Гуревича, Кубелки и Мунка коэффициент рассеяния учитывает не полное рассеяние света во всех направлениях, а только рассеяние в на­правлении, противоположном световому потоку. Поэтому световой поток, получившийся в результате рассеяния потока i, должен быть ’ прибавлен к потоку /, а световой поток, получившийся за счет рас­сеяния потока /,— к потоку L Таким образом, для изменения светового ’ потока при прохождении через элементарный слой dx можно написать цифференциальное уравнение:

di—Kidx-Sidx + Sidx или d/« — {/(+S) i dx + Sj dx. (1.22)

Аналогично изменение светового потока / можно записать:

"-.-(K+sj/rfx+su*. (1.23);

Кубелка и Мунк решили эти дифференциальные уравнения, введя { коэффициент отражения R для условия бесконечно толстой пленки, т. е. для условия, когда поток / не доходит до подложки; они получили связь коэффициента отражения с коэффициентами поглощения и рассеяния:

K/S-d.-OVW-), . (1-24) ;

где Rm — коэффициент отражений бесконечно толстой пленки, г. е. такой пленки, увели чение толщины которой уже не влияет на коэффициент отражения.

Рис. 1.9. Прохождение света через элементарный слой.

Таким образом, как видно из уравнения (1,24), —3!————- _

уменьшение функции K/S приводит к увеличению____________________________ [I 41 |_

коэффициента отражения R, а следовательно, и к ро — ~ I.

сту укрывистости. Отсюда следует, что для светлых,*"**……………………………………………………………………

пигментов, укрывистость которых определяется "ю//мгш*гжя’л главным образом отражением, желательным является как можно большее значение коэффициента рассеяния. Коэффициент рассеяния S можно вычислить, зная коэффициент отражения пигментированного слоя опре­деленной толщины, нанесенного на черное основание R, и коэффициент отражения слоя бесконечно большой толщины /?«,:

_ 1 °оо 1 — RxR оо

* -Rlo 1-Я*/Я«, ‘ (1,25)

где х — толщина слоя.

Кроющая способность лакокрасочного материала D пропорцио­нальна коэффициенту рассеяния S:

D = aS, * (1.20}

где a— коэффициент, численно равный кроющей способности при S»l; а определяется как сложная функция a=f (R, #ч, Re). Для определения коэффициента а применяются специальные номограммы, составленные Л. Галлем и М. Кремером.

В случае хроматических пигментов значения коэффициентов рассея­ния и поглощения, а следовательно, и коэффициентов отражения, раз­личны для разных длин волн, поэтому при значениях необходимо указы­вать, для каких длин волн они определены. Хроматические пигменты, обладающие кроющей способностью, должны иметь высокий коэффи­циент рассеяния только в минимуме поглощения, так как рассеяние света в максимуме поглощения приводит к снижению чистоты цвета. Пигменты, не обладающие кроющей способностью, так называемые лессирующие, имеют низкие коэффициенты рассеяния в видимой обла­сти спектра и недостаточно высокие для обеспечения кроющей способ­ности коэффициенты поглощения. Чтобы цветные красочные пленки с такими пигментами были укрывистыми, в них добавляют пигменты, обладающие высокими коэффициентами,.рассеяния; роль лессирующих пигментов сводится только к селективному поглощению света и при­данию, соответственно, определенной окраски пленке.

Рассеяние света частицами пигмента обусловлено разностью пока­зателей преломления пигмента и среды, в которой он диспергирован. Если пигмент состоит из крупных частиц, значительно превышающих по размерам длины волн видимого света, рассеяние сводится к много­кратному зеркальному отражению светового потока поверхностями частиц. При нормальном падении монохроматического света из среды с коэффициентом преломления т в среду с коэффициентом преломле­ния л2 коэффициент отражения R определяется уравнением Френеля:

*-1(И|-п,)/(л,+яд)19. (1.27)

Если же частицы пигмента соизмеримы с длиной волны, рассеяние света не подчиняется этому закону.

При прохождении света через однородную среду все частицы под­вергаются поляризации, зависящей от частоты электромагнитных коле­баний. В результате поляризации образуются диполи с переменным электрическим моментом, которые тоже излучают свет, т. е. сами яв­ляются источниками электоомагнитных колебаний. Согласно поиниипу

Гюйгенса, свет, излучаемый диполями, распространяется в том же направлении, что и падающий поток, с интенсивностью падающего потока. Если в системе присутствуют частицы с большей или меньшей поляризуемостью, чем среда, а показатель преломления этих частиц отличается от показателя преломления среды, то диполи, получающиеся в результате поляризации, имеют другие значения дипольных моментов. Излучение этих диполей не равно излучению среды. Такое некомпенси­рованное излучение представляет собой рассеянный свет, интенсивность которого для сферических непоглощающих частиц определяется уравне­нием Рэлея: где /$ — интенсивность рассеянного света, h — интенсивность падающего света, v — частичная концентрация, d — диаметр частиц, п и по — показатель преломления частицы и среды соответственно; К — длина волны падающего света

Уравнение Рэлея справедливо только для непоглощающих свет частиц, диаметр которых не больше 0,07 мкм.

Теория рассеяния света поглощающими свет частицами была раз­работана Ми. Уравнение для расчета интенсивности рассеянного света /s по теории Ми имеет следующий вид:

где / — расстояние от частицы до точки измерения интенсивности; и=2ж2/Я, т — комп­лексный показатель преломления, т = п (1—iK) {К —коэффициент поглощения, t = =д/ — 1 ); в — угол между направлениями рассеянного и падающего света

По теории Ми интенсивность рассеянного света для данной длины волны и данного размера частиц определяется не только соотношением показателей преломления частицы и среды, но и коэффициентом погло­щения.

Согласно теории Рэлея и теории Ми, рассеяние света возрастает с ростом показателя преломления частиц дисперсной фазы (точнее с ростом разности" показателей преломления дисперсной фазы и дис­персионной среды). Действительно, кроющая способность белых пигмеи-, тов с ростом показателя преломления п сильно возрастает:

Диоксид титана (рутил) 2,72 30,1

Диоксид титана (анатаз) 2,55 23,6

Сульфид цинка 2,37 11,8

Оксид цинка 2 05 4,1

Свинцовые белила 1,94—2,09 3,1—5,1

Возможно получение кроющих покрытий без пигментов за счет формирования в красочной пленке пузырьков воздуха. В этом случае рассеяние света происходит благодаря превышению показателя прелом­ления среды над показателем преломления воздушного пузырька.

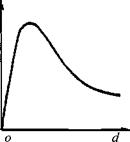
Как следует из теории Рэлея и теории Ми, рассеяние света зависит от размеров частиц. Согласно теории Ми, зависимость светорассеяния от размеров частиц выражается кривой с максимумом. Максимум свето-Л рассеяния наблюдается для частиц с размерами 0.25А,— 0,ЗЗХ Зависи­мость рассеивающей способности пигментированного слоя от размеров частиц пигмента представлена на рис. 1.10.

INK 1 10. Зависимость рассеивающей способности покрытия от Jj р. ммеров частиц пигмента

Оптимальный с точки зрения укрывистости размер частиц белых пигментов d (в нм) опре — а-ляется следующим соотношением:

d = V[2,16 (n,-n0)]. (1.30)

Из этого уравнения следует, что чем выше показатель преломления пигмента, тем выше

• юпень дисперсности, необходимая для достиже­ния максимальной укрывистости.

Определенное влияние на укрывистость оказывает и форма частиц пигмента. В частности, более высокой укрывистостью обладают пиг — н’нты, частицы которых имеют игольчатую или чешуйчатую форму. Частицы пигмента такой формы характеризуются более плотной упа — мжкой в покрытии. Чешуйчатые частицы способны к листованию, i е. к расположению в пленке параллельно ее поверхности, за счет чп о происходит полное перекрытие светового потока.

Укрывистость пигмента зависит от его объемного содержания в по — i рытии. Для каждого пигмента и конкретного типа пленкообразователя

• мцествует определенное объемное наполнение, при котором достигается максимальная укрывистость. С ростом наполнения расстояние между i птицами уменьшается и увеличивается степень перекрытия светового ока. Однако при очень малых расстояниях между частицами сблизив­шиеся частицы оказывают воздействие на световой поток как одна i рупная частица, т. е. имеет место снижение эффективной частичной итцентрации пигмента в пленке. Расстояние между частицами, при ычорых несколько частиц оптически проявляют себя как одна, прини­мают равным половине длины волны света. Отсюда следует, что для нктижения высокой укрывистости необходимо как можно более равно­мерное распределение пигмента в пленке.

Существует ряд методов экспериментального определения укрыви — ‘ юсти. Визуальный метод основан на определении толщины красоч­ною слоя на стеклянной пластинке, при котором перестают просвечи — иа гь белые и черные квадраты, нанесенные на подложку, на которую накладывается пластинка. Толщина кроющего слоя может быть опреде — п’на экстраполяцией зависимости коэффициента контрастности, опре — и-ленного инструментально, от толщины слоя пигментированного мате­риала, нанесенного на черно-белую подложку, к значению /?,//?в —0,98. lie пользуются инструментально-математические методы, основанные на жухконстантной теории Гуревича, Кубелки, Мунка с расчетом кроющей

• нособности на ЭВМ.