Лако-красочные материалы — производство

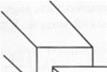
Рассмотрим случай, показанный на рис. 4.3. В этом оригинальном эксперименте упругий материал, имеющий единичную площадь поперечного сечения, подверга­ется воздействию растягивающею усилия. При разрушении материала образуют­ся две новые поверхности. Так как материал является абсолютно упругим, работа, приложенная к образцу, затрачивается только на образование новой поверхности. Принимая во внимание допущения, что обе поверхности разрушенного материала имеют один и тот же состав, можно записать уравнение в виде

U^-2y, (4 30)

где XV. определяют как работу сил когезии.

Данное уравнение принципиально имеет тот же смысл, что и результаты анали­за Фаулера-Гуггенхайма, которые были использованы для получения уравнения (1.26). Можно понять выражение, представленное уравнением (4.30), если правиль­но представить, что единственный предмет, рассматриваемый как воображаемый образец, к которому приложена работа, образует две новые поверхности, каждая из которых имеет единичную площадь. Нели каждая новая поверхность представляет собой один и тот же материал, общая затраченная энергия должна быть вдвое боль­ше поверхностной энергии материала.

Поверхность раздела между ралнорол — кыыи материалами или какая-то вообра­жаемая поверхность, находящаяся внутри монолитного материала

Рис. 43. Диаграмма, являющаяся основой дія расчета работы сил когезии и адгезии. Мо­нолитный материал разрушается с образованием двух поверхностей единичной плошали. Принимают, что материалы являются нсііоглошаюіпими и нсрассси* кающими энергию, т е. представляют собой абсолютно упругие вещества

Ранее была рассмотрена аналогичная ситуация при определении скорости осво­бождения энергии деформации. Для понимания этого необходимо вспомнить вопро­сы. изложенные в разделах 2.4 и 3.5.1.2. При выводе уравнения скорости освобож­дения энергии деформации рассматривалось явление распространения трещины в каком-либо теле. Что происходит, когда расп|юстраняется трещина? Образуются две новые поверхности! Таким образом, для случая совершенного упругого материа­ла можно записать:

В этом уравнении нижний индекс с относится к «критическому состоянию* ма­териала, в то в|>с. чя как верхний индекс С относится к упругой деформации мате­риала Остальные символы параметров приведены в гл. 2 и 3. Данное уравнение показывает, что трещина распространяется в эластичном материале в том случае, когда энергия деформации оказывается больше поверхностной энергии материала. Этот параметр известен как критерий разрушения Гриффита (13) и представлял собой первое предложенное решение данного вопроса. Гриффит с сотрудниками установили, что всего лишь некоторые материалы имеют такую малую скорость освобождения энергии де<|юрмирования, как работа когезии, причем одним из ти­пов таких материалов являкггся нешлихтованные стеклянные волокна. Установле­но. что большинство материалов не подвержены хрупкому или упругому ха|»актсру разрушения, а поглощают энергию различным образом, в том числе п|н>являя вяз­коупругие свойства. Поведение лишь нескольких материалов подчиняется крите­рию разрушения Гриффита

Представим себе ситуацию, в которой два разнородных материала находятся в непосредственном контакте. Растяг ивающее усилие разделяет образец на два разно [юдных материала. Если образец имеет единичную площадь поперечного сечения, то затрачиваемая энергия должна была бы іі|к>дстпвлять сумму двух поверхностных энергий. Однако это является неполным описанием данного воображаемого экспе­римента. Так как два различных материала находились в контакте, в этом случае существовали межмолекулярные силы, которые теперь отсутст вуют. поскольку ма­териалы были разделены. Другими словами, свободная энергия единицы поверхно­сти раздела присутствует в образце до тех пор. пока материалы не отделяются друг от друга. Поскольку эта энергия исчезает после їхазделения двух поверхностей, не­обходимо вычесть эту величину из энергии, использованной, viя образования двух новых поверхностей:

«32)

где 1Г, — работа сил адгезии; у— поверхностная энергия і — го материала: у!; — свобод­ная энергия единицы поверхности раздела между двумя материалами, находящимися в контакте.

Данное уравнение было предложено несколько веков назад и известно как урав­нение Дюпре (14). Свободная энергия единицы поверхности раздела может также рассматриваться как энергия, необходимая для создания поверхности раздела, име­ющей единичную площадь. Уравнение Дюпре играет главную роль в исследовании
явления адгезии. Необходимо отметить, что работа сил адгезии является термоди­намическим параметром. Следовательно, она не должна зависеть от таких факто­ров, как скорость, толщина клеевого слоя или каких-то других параметров, которые могут оказывать влияние на физико-механические свойства клея в блоке. Однако работа сил адгезии зависит от температуры и, как любая химическая система, от химического состава клея.

Энергию на границе раздела фаз можно также определить с помощью того же типа уравнения для простои решетки, кот орое было использовано для описания по­верхностной анергии. 11]>слположим, что два материала контактируют между собой; при этом один материал содержит атомы или молекулы, обозначенные символом А. а второй материал — атомы или молекулы под символом В. Если атомы или моле­кулы А или В находятся на іранице раздела, то атомы или молекулы А утрачивают энергию взаимодействия с некоторыми атомами или молекулами А, но сохраняют некоторую энергию взаимодействия с атомами или молекулами В. Аналогично это­му ведут себя атомы или молекулы, имеющие символ /}. Предположим, что на по­верхности раздела находятся N молекул А и В. В данном случае можно записать

(433)

где символами х — обозначены энергии взаимодействия между атомами или моле­кулами: х.,п — энергия взаимодействия между каким-то А и каким-то В на границе раздела; г — координационное число на іранице раздела; и — с]>слііяя плошать по­перечного сечения для молекулярной нары на границе раздела; Q общая площадь границы раздела; улн — энергия единицы границы раздела между жидкими фазами

При анализе уравнения (4.33) можно видеть очевидный факт, что значения меж­фазной энергии стремятся стать меньше, чем значения поверхностной энергии, так как энергетические параметры, используемые в данном выражении, взаимно вычи­таются.