Многообразные реологические свойства реальных тел можно моделировать с пбмощью различных сочетаний рассмотренных идеальных моделей. Сложные модели состоят из нескольких идеальных моделей (элементов), соединенных между собой последовательно или параллельно. При последовательном соединении элементов полная нагрузка Р приходится на каждый
Элемент, а полная деформация f или ее скорость f складываются из деформаций и скоростей составляюших элементов:
• • • •
T=Ti+T2+ ••• + 7» И 7=^1+^2+…+^ <VII.10>
При параллельном соединении элементов деформации у н
Их скорости ч одинаковы для всех элементов, а полная нагрузка складывается из нагрузок отдельных элементов:
Ї=Ї1 = Ї2= =їп И = Ъ = Ъ = … ="іп IVII.11>
С помощью этих правил сравнительно просто моделировать реологические свойства реальных тел. Для расширения возможности количественной характеристики реологических свойств реальных тел используют несколько составных идеальных моделей. Наиболее важные из этих моделей рассматриваются ниже.
Известно, что нет; принципиального различия в реологических свойствах реальных жидкостей и твердых тел. Объясняется это тем, что те и другие представляют собой конденсированное состояние вещества, характеризуемое высокой плотностью упаковки атомов и молекул и малой сжимаемостью. Жидкости и твердые тела имеют практически одинаковую природу сил сцепления, которые зависят только от расстояния между частицами. Еще Максвеллом (более 100 лет назад) было дано представление о механических свойствах тел как о непрерывном ряде переходов между идеальными жидкостью и твердым телом. Механические свойства были смоделированы Максвеллом с помощью последовательного соединения элементов Гука и Ньютона (рис. VII.5). Эта модель получила название модели Максвелла.
В модели Максвелла элементы соединены последовательно, поэтому общая нагрузка передается полностью на элементы Гука и Ньютона:
Р=РГ=Р„ (VII.12)
Общая деформация и ее скорость складываются из тех же параметров отдельных элементов:
К=Т(г+їн И df/dx=dfr/dx+d"(H/di: (VII.13>
Подставляя выражения деформаций из соответствующих законов (VII.3) и (VII.7), получим:
Р Р dy 1 dP Р
+ и — ЇГ^ІГ-ІГ+Т (VI І. 14)
Уравнения (VII. 14) являются математическим выражением модели Максвелла. Зависимость деформации от ‘времени представлена на рис. VII.5, б. Наиболее интересна эта модель для
Мгновенной и фиксированной деформации ("( = 001181 и 4 = 0). Такое состояние реализуется при мгновенном растяжении модели с сохранением в дальнейшем постоянной деформации Y — Во время удерживания постоянной деформации возникшее внутреннее напряжение постепенно снижается со временем (ре — лаксирует) вследствие деформирования вязкого элемента. При таких условиях уравнение для скорости деформации принимает вид
1 dP Р dP Е
Таг и —(УПЛ5)
Интегрирование в пределах от Ро при т = 0 до Р при т приводит к соотношению
In — ъ — (= — — т или р Fc= (VII. 16)
Го Л
Где Я = лIE — время релаксации напряжения.
Величина к представляет собой время, в течение которого начальное напряжение Ро в теле уменьшается в е раз. Зем больше к, тем медленнее рассасываются (релаксируют) напряжения в системе. Полная релаксация напряжений может произойти при т = оо. Явление релаксации, как и процесс диффузии, связано с тепловым движением молекул или частиц дисперсной фазы тела. Зависимость (VII.16) иллюстрирует рис. VII.5, В.
|
Рис. VII.5. Модель упруго вязкого тела Максвелла (а) и зависимость его деформации (б) и напряжения (при F=Const) (в) от времени |
|
Рис. VII.6. Модель вязкоупругого тела Кельвина — Фойгта (а) и зависимость деформаций при Р=Ро (Б) и при Р=0 (в) от времени |
Модель Максвелла представляет собой упруговязкую жидкость, которая может течь (релаксировать) под действием любых нагрузок. Для нее характерна необратимость деформаций. Уравнение (VII.16) показывает, что различие между жидкостями и твердыми телами не является резким и носит кинетический (релаксационный) характер. Если, например, время релаксации значительно больше времени действия напряжения, то тело называют твердым. Если же время релаксации мало по сравнению с временем действия напряжения, то тело ведет себя как жидкость—напряжения уменьшаются благодаря ее течению.
Из сказанного следует, что поведение тела определяется временем действия напряжения по отношению к времени релаксации. Покажем это на следующем примере. Если время воздействия нагрузки на типичную жидкость — воду—меньше ее периода релаксации напряжений, то течение произойти не успевает, и она ведет себя как упругое твердое тело. Струя воды (т1 = 10~3 Па-с, £=Ю10Па, А,= 10~13 с) раскалывается пулей как хрупкое тело.
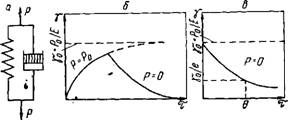
Моделью вязкоупругого твердого тела, способного восстанавливать свои свойства после снятия нагрузки (эластичность), является модель Кельвина — Фойгта. Она представляет собой соединенные параллельно элементы Гука и Ньютона (рис. VII.6, а). Для этой модели справедливы соотношения
P=*Ey + W или + (VII.17)
Что и является математическим выражением модели Кельвина — Фойгта.
Деформация ч в таком теле под действием постоянной нагрузки Р0 развивается во времени. Скорость, ее снижается, так как на упругий элемент Гука приходится все большее усилие. Когда скорость деформации уменьшится до нуля, деформация достигнет, максимального значения. При условии постоянного напряжения математическая модель тела Кельвина — Фойгта примет вид
Для решения этого дифференциального уравнения разделим переменные:
TOC o "1-3" h z _dy_ _ Л» _ А,,. ___________________ ^V___________ .
Dx ~ ц л V’ (Р0/ц)-(Е/ц)у
И далее J й1п[(Я0/1-|)-(Ј/R|)V]=A — (£/л) J Dx (VII.19) о о
Окончательное решение приводит к следующему уравнению:
Или [1-ехр(-т/0)1 (vii.20)
Где 0=ті/£ — время релаксации деформации (постоянная нагрузка), характеризующее эластичность тела.
Если снять напряжение после достижения определенной деформации, то система возвращается в исходное состояние также в течение определенного времени. Применительно к такому воздействию уравнение (VII. 18) должно быть записано без свободного члена (Ро = 0) и имеет решение, аналогичное (VII.16):
. т=То ехр [— ІЕ/ц)х] = То ехр I— т/0) (VI 1.21)
На рис. VII.6, Б, в представлена зависимость деформации у Модели Кельвина — Фойгта от времени при постоянной нагрузке Р = Р0 и изменение деформации после снятия нагрузки (Ро = 0). При снятии нагрузки тело возвращается в первоначальное состояние. В отличие от упругости (El — модуль быстрой деформации), характеризуемой мгновенными деформациями (равновесное состояние достигается со скоростью, близкой к скорости звука в данном теле), эластичность, или упругое последействие, проявляется во времени. Чем больше время релаксации деформации, тем больше эластичность тела. В качестве характеристики эластичности часто используют модуль медленной эластической деформации £2 = Р/*. Как правило, гуковские деформации твердых тел не превышают 0,1%, эластические деформации могут достигать нескольких сот процентов. Такими свойствами обладают, например, полимеры. Эластические деформации имеют энтропийный характер. Растяжение полимеров приводит к статистически менее вероятному распределению конформаций макромолекул, т. е. к уменьшению энтропии. После снятия нагрузки образец полимера самопрризвольно
Рис. VII.7. Модель вязкопластического тела Биигама (а) и зависимость деформации (б) и скорости деформации (в) этого тела от напряжения
Сокращается, возвращаясь к наиболее вероятному распределению конформаций, т. е. энтропия возрастает.
Примером тела, проявляющего вязкие или упругие свойства в зависимости от напряжения, является вязкопластическая модель Бингама. Модель Бингама представляет собой комбинацию из всех трех идеальных элементов: к соединенным параллельно элементам Ньютона и Сен-Венана — Кулона последовательно присоединен элемент Гука (рис. VII.7). В этой модели при малых напряжениях развиваются только упругие деформации, а. при достижении Р^>РТ имеет место пластическая деформация, растущая до бесконечности (течение вязкопластического тела) (см. рис. VII.7, б). Если проанализировать изменение скорости деформации в зависимости от напряжения, то окажется, что модель Бингама можно представить и без упругого элемента, деформация которого не зависит от времени. Иногда эту модель представляют только в виде параллельно соединенных вязкого элемента (модели Ньютона) и элемента сухого трения. Сложение деформаций и учет независимости упругой деформации от времени приводит к математической модели вязкопластического тела— Бингама:
|
|
(VI 1.22)
Где г)* — пластическая вязкость.
Скорость деформации равна нулю при Р<РТ, и только при Р>Рт она возрастает с увеличением напряжения (рис. VII.7, в). При Рт = 0 соотношение (VII.22) переходит в закон Ньютону. Напряжение Р разбивается как бы на две составляющие: напряжение Рт, необходимое для разрушения структуры, и напряжение Р—Рт, осуществляющее собственно течение.
По физическому смыслу пластическая вязкость отличается от ньютоновской вязкости г]. Графически она определяется котангенсом угла а наклона прямой, которая выходит из точ-
Ки P = Pr. Соотношение между ньютоновской и пластической вязкостью
Т,= (рт+Т,^)/-{=Т1*+Рт/І (VII.23)
Показывает, что ньютоновская вязкость учитывает все виды сопротивления течению тела, а пластическая вязкость, являясь частью ньютоновской, не учитывает прочности структуры, характеризуемой величиной Рт, но отражает скорость ее разрушения.
В данном разделе рассмотрены наиболее важные составные модели, позволяющие определить некоторые распространенные характеристики свойств тел. Таким же способом можно моделировать реологические свойства практически всех реальных тел, составляя довольно сложные комбинации из трех идеальных элементов.
 2 ноября, 2012
2 ноября, 2012  admin
admin 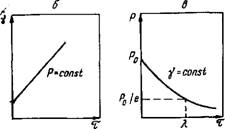
 Опубликовано в рубрике
Опубликовано в рубрике 