Коагуляция протекает в термодинамически неустойчивых (лио — фобных) дисперсных системах, и об агрегативной устойчивости таких систем судят по скорости коагуляции. Скорость коагуляции в дисперсных системах может быть самой различной. Некоторые системы коагулируют в течение нескольких секунд после их получения, а другие — устойчивы в течение суток, месяцев, а иногда и лет.
Количественная теория кинетики коагуляции была развита в трудах М. Смолуховского, Г. Мюллера, Н. А. Фукса, и других ученых. Смолуховским была рассмотрена кинетика кОагуляцИи моиоддслерсщ^_золGji_Co сферическими частйцамй^ которые" сталкиваются между собой — в результате броуновского движения. Критическое расстояние, на котором осуществляется взаимодействие между частицами, принято приблизительно равным сумме радиусов частиц, что соответствует непосредственному их контакту. Согласно представлениям Смолуховского при коагуляции происходят взаимодействия только между двумя частицами, так как вероятность одновременного столкновения большого числа частиц очень мала. Таким образом, сталкиваются частицы одиночные, образуя двойные, одиночные с двойными, двойные друг с другом, тройные с одиночными и т. д. Такое представление процесса коагуляции позволяет формально применить к нему теорию бимолекулярных химических реакций.
Чтобы определить число столкновений между частицамл, рассматривают диффузионный поток частиц через сферу, окружающую одну частицу, фиксированную в начале координат. Так как последняя тоже находится в движении, то в соответствии с теорией случайных столкновений необходимо принять, что коэффициент диффузии движущейся частицы равен сумме коэффициентов диффузии сталкивающихся п- и M-мерной частиц. (Dnm = Dn + IDm). Это следует из теории броуновского движения, в соответствии с которой относительное смещение двух частиц. Ал—Дт с коэффициентом относительной диффузии Dnm связано законом Эйнштейна — Смолуховского:
(An — Ат)а 2А„Ат А2т п
ИПт=> 21 ^ 2т — 2т 2т =IUN—RLJm
Среднее значение произведения АпАт равно нулю, так как при броуновском движении для этих частиц равновероятны движения навстречу и в разные стороны, т. е. Дя Ат с равной вероятностью может быть отрицательным и положительным.
21 Фролов Ю. Г. 321
Стационарный NotoK л-мерных частиц, средняя концентрация которых в системе равна п, через сферическую поверхность на разных расстояниях х от центральной /л-мерной частицы должен быть постоянным и равным числу столкновений частиц с этой центральной частицей. В соответствии с первым законом Фика поток через сферическую поверхность S выражается уравнением
I=Dnmsdn/dx=Dnm-4nx4n/dx (VI.4)’
Будем считать, что в выбранный за начало отсчета момент времени в единице объема находилось суммарное число vn Л-мерных частиц, что соответствует расстоянию между ними Х=оо. При столкновении частиц с центральной частицей расстояние x=Rnm (сумма радиусов частиц) и в этом месте (начало координат) концентрация частиц снижается до Vn = 0, так как предполагается, что каждое столкновение приводит к агрегации. Интегрируя уравнение (VI.4) после разделения переменных в пределах от Rnm до оо и соответственно от 0 до vn, получим:
V
Оо "П
I J dxlx2 s= inDnm j dvn *wn 0
Или
I=4nDnmRnmVn (VI.5)’
Коэффициент диффузии в соответствии с уравнением Эйнштейна (IV.42) обратно пропорционален размеру диффундирующей частицы, поэтому, если сталкивающиеся частицы не очень, сильно различаются по объему, можно приближенно считать, что произведение DnmRnm не зависит от размера частиц. Таким образом, выражение перед vn в уравнении (VI.5) является константой.
Уравнение (VI.5) отражает также число столкновений на данной стадии процесса коагуляции, т. е. число частиц, сталкивающихся в единицу времени с одной центральной частицей.. Как следует из уравнения (VI.5), число таких столкновений пропорционально общему числу частиц, находящихся в данный момент в единице объема. Число частиц, принятых за фиксированные, можно считать равным также этому числу. Таким образом, общее число столкновений между частицами « системе в единицу времени в данный момент составляет
— Rfvi/c/т=SnDRvz2 (VI.6)
Где Vj.—суммарная концентрация частиц разных размеров в данный момент.
В соотношении (VI.6) принято, ЧТО Dnm = 2D, A Rnm = R, т. е. при — няты средние величины.
Чтобы рассчитать скорость уменьшения числа частиц в результате коагуляции, т. е. скорость коагуляции, необходимо принять, что все столкновения приводят к агрегации. Однако это справедливо только тогда, когда энергия соударений частиц превышает среднюю энергию, необходимую для их слипания АЕ, называемую потенциальным барьером. Эффективность соударений пропорциональна фактору Больцмана. Проводя дальнейшую аналогию с теорией активных столкновений, необходимо учесть стерический множитель Р, учитывающий благоприятные пространственные расположения частиц при столкновении, их форму, размеры. Тогда скорость коагуляции в данный момент времени составит:
— dxz/di=&xDRP Ехр [— AE/(kBT)]vz2 (VI.7)
Сравнение с уравнением для скорости бимолекулярной реакции
— dvz/dx^Kvx2 (VI.8)
Показывает, что константа скорости коагуляции выражается следующим соотношением:
K=8nDRP ехр [— ДЕ/ (КБТ)] (.VI.9)
Общее число частиц в результате коагуляции уменьшается по закону (VI.8). Чтобы определить, каким оно будет через время т, необходимо провести интегрирование в пределах от Vi = V0 при т=0 до vi при т:
VS х
— j dvs/v2s=3 |ыт
Vo О
И
<vi-10>
Где vo — первоначальное число частиц в дисперсной системе.
Константу скорости коагуляции теоретически определить трудно, поэтому Смолуховский ввел понятие времени (периода) половинной коагуляции 0 — времени коагуляции, в течение которого общая концентрация частиц уменьшается до половины от начальной концентрации первичных (единичных) частиц. Из (VI. 10) следует:
L+#Voe=2, AV0=l/e (VI. 11)
(VI-12)
Выражение (VI. 12) дЛя концентрации частиц через время коагуляции т в теории Смолуховского широко используется для обработки экспериментальных результатов исследования кинетики коагуляции, особенно удобна для этого его линейная форма
|
21* |
|
32$ |
L/vi=l/v0+t/(v0E) (VI.13)
Общее число частиц vi в единице объема системы представляет собой уменьшающуюся в процессе коагуляции сумму частиц всех порядков:
Vs«2v!=iv1 + v!+vJ+..-!=TJ^r (VI. 14)»
Этот ряд является суммой геометрической прогрессии со знаменателем
L+т/Є ‘ = (VI.15).
Отсюда легко определить число частиц каждого порядка (/я-мерных):
= ^ 1 —J— т/0)т+1 <VM6>
Если время т равно времени половинной коагуляции, то Vi— = v0/2; vi = v0/4; V2=v0/8; v3 = v0/16 и т. д. Таким образом, зь, Время половинной коагуляции общее число частиц уменьшается вдвое, а число единичных, двойных, тройных и т. д. частиц становится равным соответственно ‘Л, Ча, ‘Л6 и т. д. от исходного числа частиц v0. На рис. VI.2 показано изменение числа vm различных частиц во времени при коагуляции. Общее число частиц Vi И число первичных чэстиц vi постоянно уменьшаются. В то же время число вторичных, третичных V2, V3, V4 н т. д. частиц сначала растет, достигает максимального значения, а затем уменьшается.
Согласно теории кинетики коагуляции различают быструю и медленную коагуляцию. Для такого разделения можно воспользоваться уравнением (VI.9) константы скорости коагуляции. При быстрой коагуляции все столкновения частиц эффективны, т. е. приводят к слипанию частиц. Быстрой коагуляции отвечает условие равенства нулю потенциального барьера Д£=0 и равенства единице стерического множителя Р— 1. Константа скорости быстрой коагуляции в соответствии с уравнением (VI.9) равна
K6=8NDR (vi. 17)
Если учесть, что R = 2r, D=kBTf(6nir) То
Кб=8*вг/зп (vi. 18)
Что составляет 1,07- 10~" см3 на частицу за 1 с в воде или 5,86- *10~10 см3 на частицу за 1 с при 20ЯС в воздухе.
Время половинной коагуляции с учетом (VI. 11) составит
Рнс. VI.2. Изменение числа частиц во времени при коагуляции по Смолуховскому
Из соотношения (VI. 18) следует, что константа скорости быстрой коагуляции зависит только от температуры и вязкости среды. Вязкость жидкостей, как правило, уменьшается с повышением температуры, что обусловливает тем самым резкую зависимость константы скорости коагуляции от температуры. У газов с повышением температуры вязкость увеличивается, поэтому зависимость константы скорости коагуляции в системах с газообразной дисперсионной средой от температуры выражена менее заметно. Время половинной коагуляции [см. уравнение (VI. 19)], кроме того, уменьшается с ростом концентрации дисперсной системы. Агрегатив — ная устойчивость систем соответственно повышается с увеличением вязкости дисперсионной среды, понижением температуры и концентрации дисперсной фазы.
Необходимо отметить, что теория кинетики быстрой коагуляции Смолуховского была блестяще экспериментально подтверждена Зигмонди, а затем и другими учеными, несмотря на некоторые ее допущения. Теория исходит из того, что золь имеет сферические монодисперсные частицы, хотя на практике это встречается очень редко. Кроме того, предполагается, что монодисперсность приблизительно сохраняется и во время коагуляции.
Теория быстрой коагуляции полидисперсных золей была развита Мюллером, она является продолжением теории Смолуховского. Основной вывод этой теории, подтвержденный экспериментально, заключается в том, что полидисперсные системы коагулируют быстрее, чем монодисперсные. Крупные частицы выступают в роли зародышей коагуляции: в их присутствии мелкие частицы исчезают быстрее, чем в их отсутствие. Теория Мюллера объяснила и некоторое возрастание скорости коагуляции в монодисперсных золях вследствие увеличения их полидисперсности в ходе коагуляции. Мюллером было также показано, что плоские частицы коагулируют с такой же скоростью, что и сферические. Частицы, имеющие форму палочек, должны коагулировать быстрее.
Для медленной коагуляции АЕфО, РФ 1 (необходимо учитывать эффективность соударений). Исходя из уравнений (VI.9), (VI.17) и (VI.18), константу скорости медленной коагуляции можно выразить так:
|
|
Я„=КбЯехр[— Д£/(ЙБЛ] ‘ VI.20»
(IV.21)
Связь эффективности соударений с потенциальным барьером при коагуляции была показана Н. А. Фуксом. Если АЕ значительно больше ksТ, то скорость коагуляции приближается к нулю, и система окажется агрегативно устойчивой. В теории, развитой Н. А. Фуксом, используется представление о коэффициенте замедления W, который показывает, во сколько раз константа скорости медленной коагуляции меньше константы скорости быстрой коагуляции. Учитывая соотношение (VI.20), получим:
К I
W =» =»-р- ехр [ АЕ/(K^T) ] (VI .22)
Коэффициент W иногда называют фактором устойчивости или коэффициентом стабильности.
 2 ноября, 2012
2 ноября, 2012  admin
admin 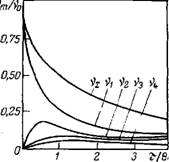
 Опубликовано в рубрике
Опубликовано в рубрике 