Цветовой тон может быть выражен, как было указано на стр. 40, величиной раздражения красных, зеленых и синих нервных центров.
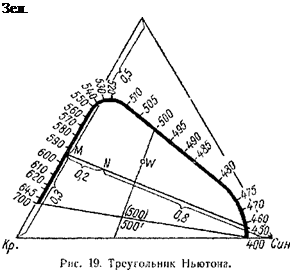
Ньютон предложил для графического изображения цветов пользоваться равносторонним треугольником, в вершинах которого находятся красный, зеленый и синий цвета (рис. 19). Положение всякого цвета на площади такого треугольника определяется одной точкой, которая может быть найдена, если известны величины раздражения красных, зеленых и синих нервных центров.
Положение цвета на площади треугольника находят, пользуясь аналогией с нахождением центра тяжести трех грузов, подвешенных в вершинах треугольника.
При определении местоположения цвета на площади треугольника вместо грузов в расчет принимают раздражения красных, зеленых и синих нервных центров. Предположим, что эти раздражения для какого-нибудь цвета равны: R — 0,5, G = 0,3 и В ~ 0,2, Применяя правило для нахождения центра тяжести, можно по величине раздражений нервных центров найти на площади треугольника положение цвета, вызывающего эти раздражения.
Цвет, вызывающий раздражение R ~ 0,5 и G — 0,3, расположен, очевидно, на прямой, соединяющей вершины треугольника, в которых расположены красный и зеленый цвета, т. е. на красно — зеленой стороне треугольника. Точка, в которой находится этот
цвет, отстоит от красной и зеленой вершин на расстоянии, обратно пропорциональном раздражениям красных и зеленых центров, т. е. в точке М величина этого раздражения равна 0,5 + 0,3 = 0,8. Точно так же найдем точку, в которой получается раздражение, равнодействующее найденному, и В — 0,2. Эта точка лежит на прямой, соединяющей точку М с синей вершиной треугольника, на расстоянии, обратно пропорциональном величине раздражений, т. е. в точке N. Величина раздражения, соответствующего этой точке: 0,8 + 0,2 = 1,0.
 |
Таким образом точка, определяющая цвет с характеристикой R = 0,5, G = 0,3 и В = 0,2, поместится на площади треугольника
в точке N. В этой точке расположится только один этот цвет. При малейшем изменении хотя бы одного раздражения точка, определяющая положение цвета на площади треугольника, переместится; И наоборот, если известно положение точки на площади треугольника, то можно найти величины трех раздражений, которые определяют положение этой точки на площади.
Так, например, зная положение точки N, проводим через нее и синюю вершину треугольника прямую. Определив по чертежу, что расстояние MN в четыре раза меньше, чем расстояние от N до синей вершины, и разложив раздражение, равное 1, на величины, обратно пропорциональные этим расстояниям, мы найдем, что раздражение, соответствующее точке N, можно разложить на два раздражения, из которых одно, равное 0,2, приложено в синей вершине треугольника, а другое, равное 0,8 — в точке М. Разложив таким же образом это раздражение (в точке М), найдем R — 0,5 и
G — ОД Следовательно, положение точки N соответствует цвету с характеристикой: R ~ 0,5; G = 0,3 и В = 0,2.
Если все три раздражения, определяющие цвет, увеличить или уменьшить в одно и то же число раз, то, как легко убедиться, положение точки на плоскости треугольника не изменится, а так как одинаковое изменение всех трех раздражений вызывает только изменение яркости цвета, то очевидно, что цвета одного цветового тона и одинаковой насыщенности, различающиеся между собой только по яркости, поместятся в одной точке. Следовательно, каждому из цветов, между которыми существует качественное различие (по цветовому тону и насыщенности), соответствует своя точка на площади треугольника; цвета же, которые различаются только количественно (по яркости), помещаются в одной точке; поэтому определить яркость цвета по положению цветовой точки в треугольнике нельзя.
В табл. 3 (стр. 42) приведены раздражения нервных центров, производимые светом различных длин волн. Пользуясь этими величинами, можно найти на площади треугольника ряд точек, из которых каждая соответствует одному из спектральных цветов. Обозначив эти точки цифрами, указывающими длину соответствующей световой волны, и соединив точки, мы получаем кривую, на которой расположены все спектральные цвета. На прямой, соединяющей концы этой кривой, расположены пурпурные цвета, которые в спектре отсутствуют и которые получаются смешением фиолетового и красного цветов.
Так как пурпурных цветов в спектре нет, то для их обозначения применяют цифры, находящиеся в месте пересечения прямой, проходящей через соответствующий пурпурный цвет и центр треугольника, с кривой. Цифры, обозначающие пурпурные цвета, для отличия от спектральных цветов либо ставят в скобки, либо помечают значком; так, спектральный цвет обозначают 500 шр, а пурпурный— либо (500 гпр), либо 500’тр.
Так как все цвета получается смешением спектральных, то точки, соответствующие всем известным цветам, располагаются внутри этой замкнутой кривой. Точка, соответствующая белому цвету, очевидно находится в таком месте, которое характеризует одинаковое раздражение красных, зеленых и синих нервных центров. Точкой, равноудаленной от трех вершин равностороннего треугольника, является его центр, или точка пересечения всех трех биссектрис. Эта точка обозначается буквой W.
На прямой, проведенной из точки белого цвета к какой-нибудь точке на кривой, располагаются цвета одного цветового тона. Этот. цветовой тон характеризуется длиной волны, которой соответствует точка пересечения этой прямой с кривой. На такой прямой, характеризующей определенный цветовой тон, располагаются цвета от белого до наиболее насыщенного спектрального. Точки на этой прямой характеризуют смеси насыщенного спектрального цвета с белым, т. е. цвета определенного тона, но разной насыщенности. Чем ближе точка находится к точке белого цвета, тем меньше на* сыщенность цвета,
В точке белого цвета насыщенность всех цветовых тонов равна нулю; на наружной же кривой находятся точки, соответствующие наиболее насыщенным цветам. Таким образом, расстояние от
|
Рис. 20. Цветовой график в системе координат: а—ультрамарин высшего сорта; 16— ультрамарин низшего сорта; /е —ультрамарин среднего сорта; 2 — титановые и литопонные белила; 3— цинковые белила; 4 — крон лимонный; 5 —крон желтый; 6— охра; 7 — умбра жженая; 3— крон оранжевый; 9 —литоль шарлах; 10 — окись хрома; 11 — марганцовая фиолетовая. |
точки белого цвета до точки определяемого цвета характеризует насыщенность последнего.
Если провести прямую через точку белого цвета в обе стороны до пересечения с кривой, то точки пересечения соответствуют цветам, являющимся дополнительными. Действительно, цвет, получаемый смешением двух цветов, находится на прямой, соединяющей эти цвета. При смешении же дополнительных цветов получается белый цвет, следовательно, прямая, соединяющая два дополнительных цвета, должна проходить через точку белого цвета.
Все цвета, которые нам известны, находятся на участке треугольника, ограниченном кривой, так как цветов, более насыщенных, чем спектральные, не существует. Поэтому на практике для графических изображений и расчетов пользуются не треугольником Ньютона, а только его частью, ограниченной кривой, на которой нанесены цифры, соответствующие длинам волн {рис. 20).
Внутри этой кривой наносится ряд подобных кривых, которые служат для определения менее насыщенных цветов. Цифры на этих кривых характеризуют насыщенность цвета в процентах. Каждая прямая, идущая из точки белого цвета к любой точке спектрального насыщенного, находящегося на наружной кривой, определяет различные степени насыщенности одного цветового тона. Весь график располагают вместо треугольника в системе координат, где по оси X отложены раздражения красных нервных центров, т. е. R, а по оси У — зеленых, т. е. G.
Раздражение синих центров определяется как дополнение до 1, т. е. из равенства Z = 1 — (X + К). Точка белого цвета в таком графике должна быть расположена на координатах X — 0,333; Y — 0,333 и, следовательно, Z ~ 0,333.
На рис. 20 точка белого цвета находится на пересечении координат X = 0,35; У “ 0,35 и, следовательно, Z = I — (0,35 + 0,35) — = 0,3, так как на практике приходится пользоваться не идеальным белым цветом, а цветом, которому соответствует точка с координатами: X « 0,35; У — 0,35 и Z «= 0,3.
На рис. 20 очерчены области, в которых располагаются цвета некоторых пигментов.
 18 августа, 2015
18 августа, 2015  admin
admin 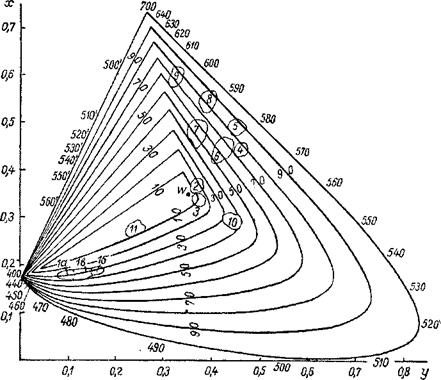
 Опубликовано в рубрике
Опубликовано в рубрике 