Анализ дисперсности веществ и материалов люди проводили с древних времен. Еще в далеком прошлом была известна роль дисперсности (которую в то время определяли на ощупь) для кроющей способности и яркости красок, для вкусовых качеств муки, для получения мелкозернистых кирпича, фарфора. В настоящее время дисперсность служит одним из основных технологических параметров веществ и материалов во многих производствах. Разработаны различные методы дисперсионного анализа, из которых наиболее простой и распространенный метод — седиментационный.
Принцип седиментационного метода анализа дисперсности состоит в измерении скорости осаждения частиц, обычно в жидкой среде. По скорости осаждения с помощью соответствующих уравнений рассчитывают размеры частиц. Метод позволяет определить распределение частиц по размерам и соответственно подсчитать их удельную поверхность. Седиментационный метод анализа дисперсности в гравитационном поле применим для анализа микрогетерогенных и некоторых грубодисперсных систем. Он позволяет определять размеры частиц в интервале от Ю-5 до Ю-2 см, которому соответствуют суспензии, эмульсии, порошки — дисперсные системы, наиболее распространенные и важные в различных областях промышленности.
Размер частицы дисперсной фазы обычно характеризуют радиусом частицы, реже объемом или площадью ее поверхности. Радиус однозначно определяется только, дЛя частиц сферической формы. Для частиц неправильной формы радиус — условная величина и его значение зависит от экспериментального метода измерения. Так, с помощью микроскопа определяют несколько линейных размеров частицы и среднее значение принимают за ее радиус. Часто при микроскопическом анализе за радиус частицы принимают радиус круга, площадь которого равна площади проекции частицы на плоскость, перпендикулярную оси оптической системы микроскопа. При кондуктометрическом методе дисперсионного анализа, например, с помощью счетчика Колтера, в качестве радиуса частицы используют радиус сферы с тем же объемом, что и объем частицы. При седиментацион — ном анализе, как уже упоминалось, размер частицы определяют как радиус сферической частицы той же плотности, оседающей со скоростью, равной скорости движения частицы (гидравлический радиус).
Чтобы уравнения седиментации одной частицы были применимы для всей совокупности частиц дисперсной системы, должно выполняться условие независимости движения каждой частицы. Такое условие достигается в разбавленной системе, а иногда при введении специального стабилизатора, предотвращающего слипание частиц.
Принцип седиментациониого анализа удобно рассмотреть на примере монодисперсных систем, которые служат хорошей простейшей моделью для изучения седиментации. В монодисперсиой системе все частицы осаждаются с одинаковой скоростью. В соответствии с этим такую же скорость перемещения имеет граница осветления, концентрация частиц по уменьшающейся высоте столба суспензии сохраняется постоянной и также с постоянной скоростью увеличивается масса осевших частиц. Если. Q — общая масса дисперсной фазы, Н—первоначальная высота столба суспензии, например, в цилиндре, то QjH — масса дисперсной фазы в объеме, приходящаяся на единицу высоты столба суспензии. При скорости осаждения частиц и в течение времени т вещество осядет из столба высотой их, и масса осевшего вещества составит
Т i= —Jj— их (IV.19)
Это уравнение описывает кинетику седиментации в монодисперсной системе. Так как величины Q, Я и и постоянны, то масса осевших частиц из монодисперсной системы пропорциональна времени седиментации. Эта линейная зависимость представлена на рис. IV. 1 а. Точке В соответствует окончание процесса седиментации и в последующие моменты времени масса осевших частиц не изменяется. Тангенс угла наклона прямой характеризует скорость оседания дисперсной фазы. Если принять, что
Частицы имеют сферическую форму и при их осаждении соблюдается закон Стокса, то, используя формулу (IV.7), получим:
|
9тНт |
— — (IV.20)
9т)Я
Отсюда радиус частицы равен
Таким образом, определяя экспериментально зависимость массы осевшего осадка от времени, можно рассчитать размер частиц. Соотношения (IV.20) и (IV.21) выполняются при соблюдении всех перечисленных в предыдущем разделе условий, при которых применим закон Стокса.
Если известен радиус частиц, можно рассчитать удельную (по массе) поверхность порошка sya по соотношениям (111.61):
5уд=3/(гр)
|
Т |
В отличие от поведения частиц в монодисперсных системах частицы в полидисперсных системах осаждаются с разными скоростями, поскольку они имеют неодинаковые размеры. В основу дисперсионного седиментационного анализа полидисперсных систем положено представление о том, что системы состоят из нескольких фракций, которые можно рассматривать как отдельные монодисперсные системы. Очевидно, чем на большее число фракций разделена полидисперсная система, тем в большей степени эти фракции будут соответствовать монодисперсным системам и тем с большим основанием для них могут быть использованы соотношения (IV.20) и (IV.21).
При седиментациониом анализе дисперсности полидисперсных систем определяют время осаждения частиц отдельных фракций, по уравнениям (IV.7), (IV.8) и (IV.21) рассчитывают скорости их осаждения и соответствующие им размеры частиц. Для этого сначала измеряют зависимость массы осевшего осадка от времени, строят график этой зависимости, называемой Кривой седиментации, по которому затем определяют все необходимые характеристики дисперсной системы.
Имеются графические и аналитические методы расчета кривой седиментации. Несмотря на большую точность аналитических методов, здесь рассматривается один из графических методов как наиболее наглядный, и простой. Выше показано, что процесс седиментации монодисперсной системы графически нырджается прямой (см. рис. IV.1а).
Для полидисперсной системы осаждение каждой фракции описывается отдельными прямыми, представленными на рис. IV.1 б: OA, OB, ОС и OD. Чем меньше размер частицы, тем меньше наклон прямой. Массу суммарного осадка, выпавшего ко времени т, можно представить соотношением:
111=—It |Т + /?2Т + £3Т+ ■ • ■ =(k,-lrk2+k3+ . . . )Т где І’,- — коэффициент пропорциональности.
Этому соотношению отвечает участок кривой седиментации OA’ После выпадения первой фракции указанное соотношение принимает следующий вид
M — mі + </г2 + /г3+ .. . W
!іто соответствует участку А’В’ кривой седиментации. Экстраполяция этого участка на начало осаждения дает свободный член nil, означающий массу частиц первой фракции. После выпадения второй фракции получим:
Ш = (/Н| + M2) + (K3 + K4+ . . . )т
Экстраполяцией можно получить свободный член на оси ординат н соответственно массу частиц второй фракции. Продолжая указанные операции, можно найтн массу частиц третьей
И последующих фракций. Тангенс угла наклона линейных участит
Ков ломаной кривой седиментации tgA = Am/Ax = K, где K = 1K;
І
Определяет скорость накопления массы осадка в данный отрезок времени.
Реальная кривая седиментации полпдисперсной системы обычно получается плавной (см. рис. IV. 1 в) и ей отвечает множество бесконечно малых участков, касательные в каждой точке этой кривой отражают седиментацию данной бесконечно малой фракции. Уравнение касательной в любой точке кривой Седиментации по аналогии с предыдущими соотношениями имеет вид
Dm
M^mi-u-jf Ті (IV.22}
Это уравнение называется уравнением Одена. Оно является обоснованием графического метода расчета распределения частиц по размерам в полидисперсных — системах. Этот метод заключается в том, что экспериментальную кривую седиментации полиднсперсной системы (см. рис. IV.в) делят на участки, соответствующие выбранным временам полного осаждения фракций (тмии, Т2, тз-.тмакс). Такое разделение кривой лучше проводить после предварительного определения времени осаждения самой крупной и самой мелкой фракций. Полному осаждению самой крупной фракции отвечает тмнн, время осаждения самой мелкой фракции соответствует времени окончания накопления осадка тМако В точках кривой, отвечающих моментам окончания осаждения фракций (А, В, С, D), проводят касательные до ПеРесечения с осью ординат, на которой получают отрезки, соответствующие массам фракций частиц. Зная высоту столба суспензии и время полного осаждения фракций, по формуле (IV.19) можно определить скорость осаждения и по формулам (IV.8) и (IV.21) рассчитать радиус частиц каждой фракции. Очевидно, чтр применительно к полидисперсным системам этот радиус является граничным для соседних фракций, а средний радиус фракции тем ближе отражает истинное значение, чем на большее число фракций разделена полидисперсная система.
Результаты седиментационного анализа дисперсности полидисперсных систем представляют также в виде кривых распределения частиц по размерам, характеризующих степень полидисперсности системы.
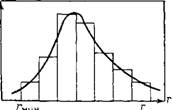
Кривая распределения является наглядной и удобной характеристикой полидисперсности системы, по которой легко определить содержание различных фракций. Ее строят подобно кривой распределения пор по размерам, описанной в разд. III. Б. Обычно сначала получают интегральную кривую распределения, проводят ее выравнивание с учетом точности получаемых средних значений радиусов частиц фракций и затем по йен строят дифференциальную кривую распределения. Иногда дифференциальную кривую строят сразу. Такое построение показано на рис. IV.2. На оси абсцисс откладывают значения радиусов; на ось ординат наносят отношение приращения массовых долей к разности радиусов частиц соседних фракций Ддс/Дт-,-. Построив на графике отдельные прямоугольники для кажіїой фракции (гистограмму) и соединив плавной кривой середины их верхних сторон, получают дифференциальную кривую распределения частиц полидисперсной системы по размерам. Чем
Рис. IV.2. Дифференциальная кривая распределения частиц полидисперсной системы по радиусам
Меньше отличается Гмнн от Гмакс И чем больше максимум кривой распределения, тем ближе система к монодисперсной.
|
ЛХ/АГі |
|
Макс |
Количественно дисперсность полидисперсных систем выражают через средние значения радиусов частиц, их массы, объема, молекулярной массы и других параметров. Различают три способа расчета средних значений этих параметров: среднечисленное значение
|
(IV.23) |
|
2 я» |
|
2 я’ |
У^ХЧіУІ
|
(IV.24) |
|
S піх%і |
Среднеповерхностное значение 2 ПІ*гіУі ^
У я,-
|
(IV.25) |
|
2 "і**і |
Среднеобъемное или среднемассовое значение 2 "Ix3YI Vn
■ Yi t= 2 ХмІУі
2 "і*3.-
Где У— величина, среднее значение которой (V) рассчитывается; пі — число частиц в данной фракции; х, — размер частиц <-й фракции; Хч Х„ Х„ — соответственно численные, поверхностные и объемные (массовые) доли от общего числа частиц, их поверхности и объема (массы).
Порядок расчета по представленным соотношениям понятен из их записей. Если нужно определить, например, среднеповерх — ностный диаметр частиц в полидисперсной системе, то воспользовавшись формулой (IV.24), получим:
2 п Id* id І —, п, (Pi
В монодисперсной системе величины Усч, Yen, YCM имеют одинаковые значення, а в полидисперсной системе они различны. Чем выше полидисперсность, тем сильнее различаются эти величины. Такая закономерность обусловлена относительным возрастанием удельной поверхности и еще сильнее — числа частиц в единице массы или объема по сравнению с удельным объемом
(или массой) при уменьшении размера частиц. Поэтому часто полидисперсность систем характеризуют отношением
/7 = Гс„/Гс„ UV.27)
Это соотношение всегда меньше единицы; для монодисперсной системы оно равно единице.
Необходимо отметить, что различные методы определения размеров частиц могут давать неодинаковые значения среднего размера. Это связано с тем, что принципы методов определения дисперсности могут быть основаны на свойствах, зависящих от числа частиц, или от их поверхности, или от объема (массы).
 2 ноября, 2012
2 ноября, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике 