Для описания термодинамики поверхностных явлений приме няют два метода: метод избыточных величин Гиббса и метод «слоя конечной толщины». За толщину поверхностного слоя принимают расстояние по обе стороны от границы раздела фаз, за пределами которого свойства слоя перестают отличаться or свойств объемных фаз. Практически вся поверхностная энергия сосредоточена в поверхностном слое толщиной в несколько молекул, поэтому все связанные с нею соотношения можно относить только к поверхностному слою. Как следует из определения толщины поверхностного слоя, установление его границ со стороны объемных фаз представляет довольно трудную задачу. Более того, из-за чрезвычайно малой толщины поверхностных слоев погрешности при ее экспериментальном измерении могут
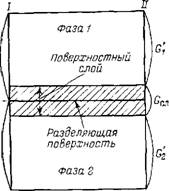
Рис. 11.3. Схема, иллюстрирующая принцип термодинамических методов избыточных величин Гиббса (I) и слоя конечной толщины (//)
Быть значительными, что, в свою очередь, приводит к неточным определениям и термодинамиче — Q-.s_ ских параметров слоев.
Чтобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин (рис. II.3, /) энергия Гиббса системы равна сумме энергий Гиббса Gi и G2 объемных фаз 1,2 и поверхностной энергии Гиббса os, которая является избыточной:
G = G, + G2+Oa— (11.22)
В методе «слоя конечной толщины» рассматривается поверхностный слой, имеющий определенные размеры (рис. II.3, 11). Его термодинамические параметры включают как поверхностную энергию os, так и энергию объема слоя Gvc.Имеющего те же свойства, что и объемные фазы (Осл = os+ Gvcn). Границы объемных фаз совпадают с границами поверхностного слоя, что отвечает фактическому началу появления неоднородности. Энергия Гиббса той же системы в методе «слой конечной толщины» выразится соотношением
G=G1’+G2′ + GCil = Gl’+ G2′ + G°Ca+os (11.231
Где Gи G2′ — энергия Гиббса соответственно фазы / и фазы 2 до границы поверхностного слоя (поверхности разрыва).
В уравнении (11.23) все параметры отвечают реальному строению системы и имеют определенный физический смысл. Однако этот метод требует знания толщины поверхностного слоя и использует довольно сложные уравнения, так как термодинамические параметры изменяются нелинейно по толщине слоя. В то же время он дает возможность определить этот °чень важный параметр поверхностного слоя. При использовании же метода избыточных величин нет необходимости опреде-
.
лять границы поверхностного слоя. Кроме того, этот метод оперирует поверхностными избытками, что упрощает математические выражения, хотя избыточные параметры зависят от положения разделяющей поверхности, которым надо задаваться. Далее используется в основном более простой и распространенный метод избыточных величин Гиббса.
В соответствии с известным термодинамическим соотношением энтальпия поверхности (ее избыток) выражается уравнением
H=G + TS (11.24)
Аналогичным выражением характеризуется избыток внутренней энергии поверхности конденсированных систем:
Us = Gs + TSs (11.25)
Где индекс s означает отнесение потенциалов к единице поверхности.
В соответствии со вторым началом термодинамики избыточная энтропия равна
Ss = Qs/T (11.26)
Где qa— теплота образования единицы поверхности (в обратимом процессе). Иногдз q„ называют скрытой теплотой образования поверхности. Она равна количеству теплоты, которое необходимо сообщить телу, чтобы при постоянной температуре увеличить его поверхность на единицу площади.
Учитывая, что Gs = c, из уравнений (11.25) и (11.26) получим следующее выражение:
Us = o + qs (II.27)
Из уравнения (11.27) следует, что внутренняя энергия поверхности складывается из энергии Гиббса и теплоты образования поверхности. Для индивидуальных веществ теплота qs всегда положительна, так как при образовании поверхности теплота поглощается. В результате внутренняя удельная поверхностная энергия (единицы поверхности) больше поверхностной энергии Гиббса на теплоту образования единицы поверхности. Поэтому ее обычно называют полной поверхностной энергией.
Из уравнения (1.2) при постоянстве всех параметров, кроме температуры Г, имеем:
RfGs=— SsdT или (dGs/dT)p=— S„=— qs/T (11.28)
Подставляя это выражение в уравнения (11.25) или (11.27), получим:
Us = a — Tida/dT)p (11.29)
Уравнение (11.29) называется уравнением Гиббса — Гельмгольца. Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностным натяжением). Из этого уравнения
|
Таблица 11.3. Температурные коэффициенты поверхностного натяжения некоторых жидкостей
|
Следует, что для определения полной поверхностной энергии необходимо знать зависимость поверхностного натяжения or температуры. Конкретную зависимость можно получить только экспериментально, однако качественные выводы можно сделать из уравнения (11.28). Как было уже указано, для индивидуальных веществ теплота Qs всегда положительна, а это значит, что температурный коэффициент поверхностного натяжения [см. уравнение (11.28)] отрицателен (табл. II.3):
T,dGs/dT)p = (do/dT)p < 0 (11.30»
Таким образом, поверхностное натяжение индивидуальных веществ на границе с газом (воздухом) снижается с повышением температуры. Для большинства неполярных жидкостей эта зависимость линейная и в первом приближении может быть аппроксимирована простым соотношением
Ог=Оо-—"АГ, откуда а = —да/дТ (11.31 >
Где пт и Со — поверхностное натяжение соответственно при температуре Т и при стандартной температуре; ДГ — разность между данной и стандартной температурами; а — постоянная, равная температурному коэффициенту поверхностного натяжения с обратным знаком.
Другие вещества менее строго следуют такой зависимости, но часто отклонениями можно пренебречь, так как температурные коэффициенты дв/дТ слабо зависят от температуры.
Зная температурный коэффициент поверхностного натяжения, по уравнению (11.29) можно рассчитать внутреннюю энергию той или иной межфазной поверхности. Например, на границе с воздухом для воды при 298 К: Us = 72—298(—0,154) « «118 мДж/м2; для ртути при 298 К: £/* = 473,5—298(—0,23) « «542 мДж/м2.
В табл. II.4 приведены значения внутренней поверхностной энергии некоторых веществ, а также теплоты образования поверхности и поверхностные натяжения. При сравнении значений величин, представленных в таблице, видно, что значительный вклад в полную поверхностную энергию вносит энтропийная составляющая— теплота образования поверхности. Для многих органических веществ она составляет около половины полной
|
Гексан |
49,5 |
18,41 |
• 31,09 |
|
Октан |
48,4 |
21.78 |
26.62 |
|
Этанол |
46,4 |
22.03 |
24,37 |
|
Октанол |
50,8 |
27,53 |
23,27 |
|
Уксусная кислота |
55,9 |
27,79 |
28,11 |
|
Масляная кислота |
54,5 |
26,74 |
27.74 |
|
Этиламин |
48.1 |
20,4 |
27,7 |
|
Пропиламии |
50.4 |
22,4 |
28,0 |
|
Вода |
118,1 |
71,95 |
46,15 |
|
Ртуть |
542,0 |
473,5 |
68,5 |
|
Таблица 11.4. Энергетические параметры поверхностей некоторых жидкостей при 298 К |
|
Вещество |
|
U.. ыДж/м; |
|
А, мДж/м3 |
|
TS,. ыДж/м: |
Поверхности энергии. Это объясняется тем, что при переходе молекул и атомов из объема тела на поверхность связи разрываются и на поверхности вещество оказывается в состоянии более близком к паровой фазе с большей энтропией, чем для вещества в других агрегатных состояниях.
Предложены нолуэмпирические соотношения более точно описывающие температурную зависимость поверхностного натяжения, чем соотношение (11.31). Так как при критической температуре о = 0 (это было показано Д. И. Менделеевым) и, как установил венгерский ученый Л. Этвеш, линейной зависимости от температуры более точно следует параметр иК.2’3 (иногда называемый мольной поверхностной энергией), то можно записать:
О У.» 2/18 = К1.Ткр — Г) (Н.32)
Где К — коэффициент пропорциональности.
Более точные наблюдения показали, что поверхностное натяжение имеет нсчезающе малые значения уже при температурах, равных Гкр — 6, поэтому уравнение (11.32) можно записать в следующей форме:
AVx-l3 = K(TKp~6 — T) (11.33)
Соотношения (11.32) и (11.33) называют законом Этвеша. Для неполярных жидкостей в СИ К = 2,1-Ю"7, для полярных жидкостей К<2,1-10-7, а для жидкостей с большой молекулярной массой К>2,1-10-7.
Очень важным является полуэмпирическое соотношение, предложенное Сагденом:
Р^Мо^/ІАр) или о= (РДр/М)й (11.34)
Где Р—величина, названная автором парахором; М — молекулярная масса жидкости; Др — разность между плотностями жидкости и пара; k—-показатель степени; в зависимости от природы жидкости может принимать значения от 3,5 до 4,5.
Из соотношения (11.34) следует: daldT~pk~’dpldT, т. е. температурный коэффициент поверхностного натяжения определяется главным образом плотностью и ее температурным коэффициентом, что можно объяснить подобием зависимостей поверхностного натяжения н плотности жидкости от межмолекуляриого взаимодействия.
Парахор Р практически не зависит от температуры. Зависимость поверхностного натяжения от температуры компенсируется изменением плотности вещества. Отсюда следует, что парахор можно рассматривать как мольный объем с поправкой на эффект сжатия, обусловленный межмолекулярнымн силами.
Для большинства жидкостей, особенно неполярных, полная поверхностная энергия также почти не зависит от температуры. Чтобы в этом убедиться, продифференцируем по температуре уравнение Гиббса — Гельмгольца (11.29):
DUs/dT = do/dT — да/дТ — Тд2о/дГ Или ди./дТ^—Тд^о/дП (11.35)
Так как для неполярных жидкостей поверхностное натяжение линейно снижается с повышением температуры, то [см. уравнение (11.31)]:
Д2<з/дТ2 = 0
Отсюда следует, что и производная полной поверхностной энергии по температуре тоже должна быть равна нулю [см. уравнение (11.35)], т. е. dUs/dT = 0, а это означает независимость полной поверхностной энергии от температуры. Для примера укажем, что вторые производные поверхностного натяжения по температуре для воды и бензола равны соответственно —0,00048 и +0,00012. Так как поверхностное натяжение снижается с повышением температуры, а полная энергия от нее не зависит, то в соответствии с уравнением (11.27) теплота образования единицы поверхности увеличивается в этом же направлении. Энтропию, как производную поверхностного натяжения по температуре со знаком минус, в таких случаях можно приравнять к постоянной а [уравнение (11.31)], которая не зависит от температуры. Температурные зависимости основных термодинамических параметров показаны на рис. 11.4. При критической температуре исчезает межфазная поверхность и соответственно снижаются до нуля ее энергетические характеристики.
От рассмотренных систем жидкость — газ существенно отличаются температурные зависимости энергетических параметров поверхностей между конденсированными фазами. Они будут рассмотрены в разделе, посвященном адгезии.
 2 ноября, 2012
2 ноября, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике 